Last Updated on March 22, 2022 by Ria Pathak

Concepts Used
Back Tracking
Difficulty Level
Hard
Problem Statement :
Given
Nintegers print all distinct combinations.
See original problem statement here
Solution Approach :
Introduction :
Idea is to swap all the values one-by-one and keep track of the values used. In a set of
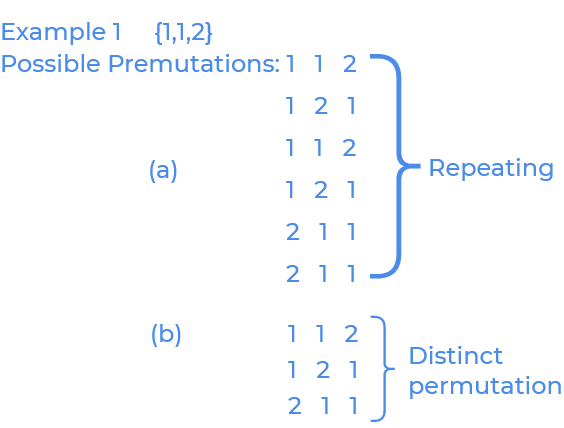
nelements withdsimilar elements there aren!/m!different permutations. For example, there are3permutations of the set {1,1,2}, namely [1,1,2], [1,2,1], [2,1,1].
Description:
We will use backtracking to solve the above problem.
Backtracking is the approach to solve the problem by testing all possible answers (by breaking the problems into subproblems). If any subproblem does not fit the given constraint then we discard the complete subproblem (backtrack), moves a step back then try other remaining possible combinations. Backtracking algorithm is generally exponential in time.
Since it has duplicate items as well, we will keep track of the items already used, with the help ofused[]array. Every time we see an unsed item we add it toused[]array. Now we will swap every index of the array, breaking our problem into subproblems by recursively calling our function for the next index, when the index becomes equal to the size of the array we print the current combination, every time we swap indices we make sure to revert the changes by swapping them back again to try another combinations (backtrack).
Algorithm :
backtracking():
- If
index == n, print the current combination. - else, for every
k= indexton-1:
- if
kis unused, addkto the used[] array - swap(index,k)
- call backtrack(arr,index+1,n)
- swap(index,k) , (Backtrack step).
- if
Complexity Analysis :
Total number of permutations are, as discussed earlier,
n!, and it takesO(n)time to print each permutation. Can you guess the final time complexity?
Solutions:
#include<stdio.h>
#include<stdbool.h>
int cmpfunc (const void * a, const void * b) {
return ( *(int*)a - *(int*)b );
}
void swap(int *x, int *y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
bool checkduplicate(int t[], int n,int id){
for(int i=0; i<n; i++)
if(t[i] == id) return true;
return false;
}
void backtracking(int nums[],int n, int index){
if(index == n)
{
for(int i=0;i<n;i++)
printf("%d \n",i);
}
int t[n];
for(int i=index; i<n; i++){
if(checkduplicate(t,n, nums[i])) // make sure nums[i] is not used
continue;
t[i] = nums[i]; // put all used items into vector t
swap(nums[i], nums[index]);
backtracking( nums,n, index+1);
swap(nums[i], nums[index]);
}
}
int main()
{
int n;
scanf("%d",&n);
int v[n];
int x;
for(int i=0;i<n;i++)
{
scanf("%d",&v[i]);
}
qsort(v, n, sizeof(int), cmpfunc);
backtracking(v,n, 0);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
bool checkduplicate(vector<int> t, int n){
for(int i=0; i<t.size(); i++)
if(t[i] == n) return true;
return false;
}
void backtracking( vector<int> nums, int index){
if(index == nums.size())
{
for(auto i:nums)
cout<<i<<" ";
cout<<endl;
}
vector<int> t;
for(int i=index; i<nums.size(); i++){
if(checkduplicate(t, nums[i])) // make sure nums[i] is not used
continue;
t.push_back(nums[i]); // put all used items into vector t
swap(nums[i], nums[index]);
backtracking( nums, index+1);
swap(nums[i], nums[index]);
}
}
int main()
{
int n;
cin>>n;
vector<int> v(n);
int x;
for(int i=0;i<n;i++)
{
cin>>v[i];
}
sort(v.begin(),v.end());
backtracking(v, 0);
return 0;
}
import java.util.*;
import java.io.*;
public class Main {
static ArrayList<String> Sarr=new ArrayList<String>();
public static void main(String args[]) throws IOException {
Scanner sc=new Scanner(System.in);
int size=sc.nextInt();
int[] arr=new int[size];
int[] freq=new int[52];
for(int i=0;i<size;i++){
arr[i]=sc.nextInt();
freq[arr[i]]++;
}
Arrays.sort(arr);
backTracking(freq,arr,"",0);
}
static void backTracking(int[] freq,int[] arr,String res,int count){
if(count==arr.length){
if(!Sarr.contains(res)){
System.out.println(res);
Sarr.add(res);
}
}
else{
for(int i=0;i<arr.length;i++){
if(freq[arr[i]]>0){
freq[arr[i]]--;
backTracking(freq,arr,res+arr[i]+" ",count+1);
freq[arr[i]]++;
}
}
}
}
}
def checkduplicate(t, n): for i in range(len(t)): if(t[i] == n): return True return False def backtracking(nums, index): if(index == len(nums)): for i in nums: print(i, end = " ") print() t = [] for i in range(index, len(nums)): if(checkduplicate(t, nums[i])): continue t.append(nums[i]) nums[i], nums[index] = nums[index], nums[i] backtracking( nums, index+1) nums[i], nums[index] = nums[index], nums[i] n = int(input()) v = list(map(int,input().split())) v.sort() backtracking(v, 0)
[forminator_quiz id="2212"]
This article tried to discuss the concept of backtracking. Hope this blog helps you solve the problem based on backtracking . To practice more problems you can check out MYCODE | Competitive Programming.


