Graph Traversal in Data Structure

Last Updated on May 5, 2023 by Prepbytes

A graph is a non-linear data structure composed of vertices and edges. Edges are lines or arcs that connect any two nodes in the network. Vertices are also known as nodes. A graph, in more technical terms, is made up of vertices (V) and edges (E). The representation of a graph is G(E, V). So, in this article, we will look at some Graph Traversal Techniques.

Graph Traversal in Data Structure

We can traverse a graph in two ways :

1. BFS ( Breadth First Search )
2. DFS ( Depth First Search )

BFS Graph Traversal in Data Structure

Breadth-first search (BFS) traversal is a technique for visiting all nodes in a given network. This traversal algorithm selects a node and visits all nearby nodes in order. After checking all nearby vertices, examine another set of vertices, then recheck adjacent vertices. This algorithm uses a queue as a data structure as an additional data structure to store nodes for further processing. Queue size is the maximum total number of vertices in the graph.

Graph Traversal: BFS Algorithm

Pseudo Code :

def bfs(graph, start_node):
    queue = [start_node]
    visited = set()

    while queue:
        node = queue.pop(0)

        if node not in visited:
            visited.add(node)
            print(node)

            for neighbor in graph[node]:
                queue.append(neighbor)

Explanation of the above Pseudocode

• The technique starts by creating a queue with the start node and an empty set to keep track of visited nodes.
• It then starts a loop that continues until all nodes have been visited.
• During each loop iteration, the algorithm dequeues the first node from the queue, checks if it has been visited and if not, marks it as visited, prints it (or performs any other desired action), and adds all its adjacent nodes to the queue.
• The operation is repeated until the queue is empty, indicating that all nodes have been visited.

Let us understand the algorithm using a diagram.

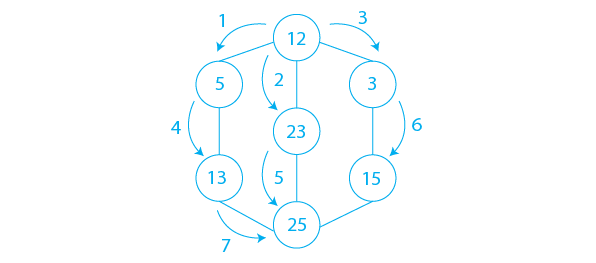
In the above diagram, the full way of traversing is shown using arrows.

• Step 1: Create a Queue with the same size as the total number of vertices in the graph.
• Step 2: Choose 12 as your beginning point for the traversal. Visit 12 and add it to the Queue.
• Step 3: Insert all the adjacent vertices of 12 that are in front of the Queue but have not been visited into the Queue. So far, we have 5, 23, and 3.
• Step 4: Delete the vertex in front of the Queue when there are no new vertices to visit from that vertex. We now remove 12 from the list.
• Step 5: Continue steps 3 and 4 until the queue is empty.
• Step 6: When the queue is empty, generate the final spanning tree by eliminating unnecessary graph edges.

Code Implementation

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            visited.add(vertex)
            print(vertex)
            queue.extend(graph[vertex] - visited)
    return visited

graph = {
    'A': {'B', 'C'},
    'B': {'A', 'D', 'E'},
    'C': {'A', 'F'},
    'D': {'B'},
    'E': {'B', 'F'},
    'F': {'C', 'E'}
}

bfs(graph, 'A')

Output :

A
B
C
E
D
F

DFS Graph Traversal in Data Structure

When traversing a graph, the DFS method goes as far as it can before turning around. This algorithm explores the graph in depth-first order, starting with a given source node and then recursively visiting all of its surrounding vertices before backtracking. DFS will analyze the deepest vertices in a branch of the graph before moving on to other branches. To implement DFS, either recursion or an explicit stack might be utilized.

Graph Traversal: DFS Algorithm

Pseudo Code :

def dfs(graph, start_node, visited=set()):
    visited.add(start_node)
    print(start_node)

    for neighbor in graph[start_node]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

Explanation of the above Pseudocode

• The method starts by marking the start node as visited and publishing it (or doing whatever additional action is needed).
• It then visits all adjacent nodes that have not yet been visited recursively. This procedure is repeated until all nodes have been visited.
• The algorithm identifies the current node as visited and prints it (or does any other required action) throughout each recursive call.
• It then invokes itself on all neighboring nodes that have yet to be visited.

Let us understand the algorithm using a diagram.

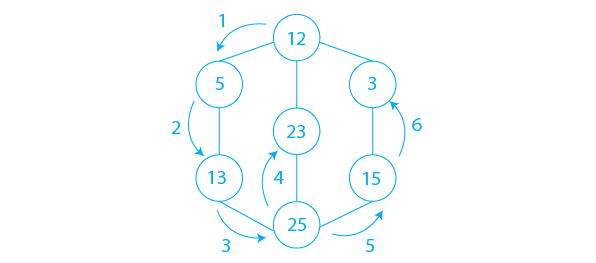
The entire path of traversal is depicted in the diagram above with arrows.

• Step 1: Create a Stack with the total number of vertices in the graph as its size.
• Step 2: Choose 12 as your beginning point for the traversal. Go to that vertex and place it on the Stack.
• Step 3: Push any of the adjacent vertices of the vertex at the top of the stack that has not been visited onto the stack. As a result, we push 5
• Step 4: Repeat step 3 until there are no new vertices to visit from the stack’s top vertex.
• Step 5: Use backtracking to pop one vertex from the stack when there is no new vertex to visit.
• Step 6: Repeat steps 3, 4, and 5.
• Step 7: When the stack is empty, generate the final spanning tree by eliminating unnecessary graph edges.

Code Implementation

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for next_vertex in graph[start] - visited:
        dfs(graph, next_vertex, visited)
    return visited

graph = {
    'A': {'B', 'C'},
    'B': {'A', 'D', 'E'},
    'C': {'A', 'F'},
    'D': {'B'},
    'E': {'B', 'F'},
    'F': {'C', 'E'}
}

dfs(graph, 'A')

Output

A
C
F
E
B
D
B

Conclusion
In this article, we have discussed the various ways of implementing graph traversal in data structures. So mainly, there are two ways of traversing graphs. I.e., BFS and DFS techniques We can also discuss these two algorithms in depth for traversal of graphs in data structures.

Frequently Asked Questions: FAQs

Q1. What are the different types of graph traversal?
Ans. There are two sorts of traversal algorithms in the graph. These are referred to as the Breadth First Search and the Depth First Search.

Q2. What is the purpose of graph traversal?
Ans. Graph traversal is a technique for finding a vertex in a graph. It is also used to determine the order in which vertices are visited throughout the search process. Without producing loops, a graph traversal finds the edges to be employed in the search process.

Q3. Which is superior, BFS or DFS?
Ans. When a user looks for vertices that remain close to a specific source, BFS performs better. DFS works better when the user can find solutions outside of any specified source. The quantity of memory required

Q4. Which algorithm is used to traverse a graph?
Ans. For traversing a graph, two methods are commonly used: depth-first search (DFS) and breadth-first search (BFS).

Q5. What are the benefits of DFS?
Ans. DFS utilizes very little memory because it only has to store a stack of nodes on the path from the root node to the current node.
It takes less time to reach the goal node than the BFS method (if it follows the correct path).