Insertion Sort in Java

Last Updated on February 19, 2024 by Abhishek Sharma

Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is efficient for sorting small arrays or nearly sorted arrays and is often used as part of more complex sorting algorithms. Understanding how insertion sort works and its implementation in Java is essential for programmers learning about sorting algorithms.

What is Insertion Sort in Java?

Insertion sort is a simple and efficient comparison-based sorting algorithm. It works by dividing the input array into two parts: a sorted portion and an unsorted portion. Initially, the sorted portion contains only the first element of the array, while the rest of the elements are considered unsorted.

The algorithm iterates through the unsorted portion of the array, taking one element at a time and placing it in its correct position within the sorted portion. This process continues until all elements are sorted, and the entire array is in order.

To better understand the steps involved in insertion sort, let’s go through a simple example using an array of integers:

1. Start with the second element (index 1) and compare it to the previous element (index 0). If the previous element is larger, swap them.
2. Move to the next unsorted element (index 2) and compare it with all the elements in the sorted portion, shifting the larger elements to the right to make space for the current element.
3. Repeat this process until all elements are in the sorted portion, and the entire array is sorted.

Insertion sort has an average and worst-case time complexity of O(n^2), making it less efficient compared to more advanced sorting algorithms like merge sort or quicksort. However, it performs well on small input sizes or partially sorted arrays and has the advantage of being an in-place sorting algorithm, meaning it doesn’t require additional memory beyond the input array.

Characteristics of Insertion Sort in Java

1. This algorithm is one of the most basic, with a straightforward implementation.
2. Insertion sort is most effective for small data values.
3. Because insertion sort is adaptive, it is appropriate for partially sorted data sets.

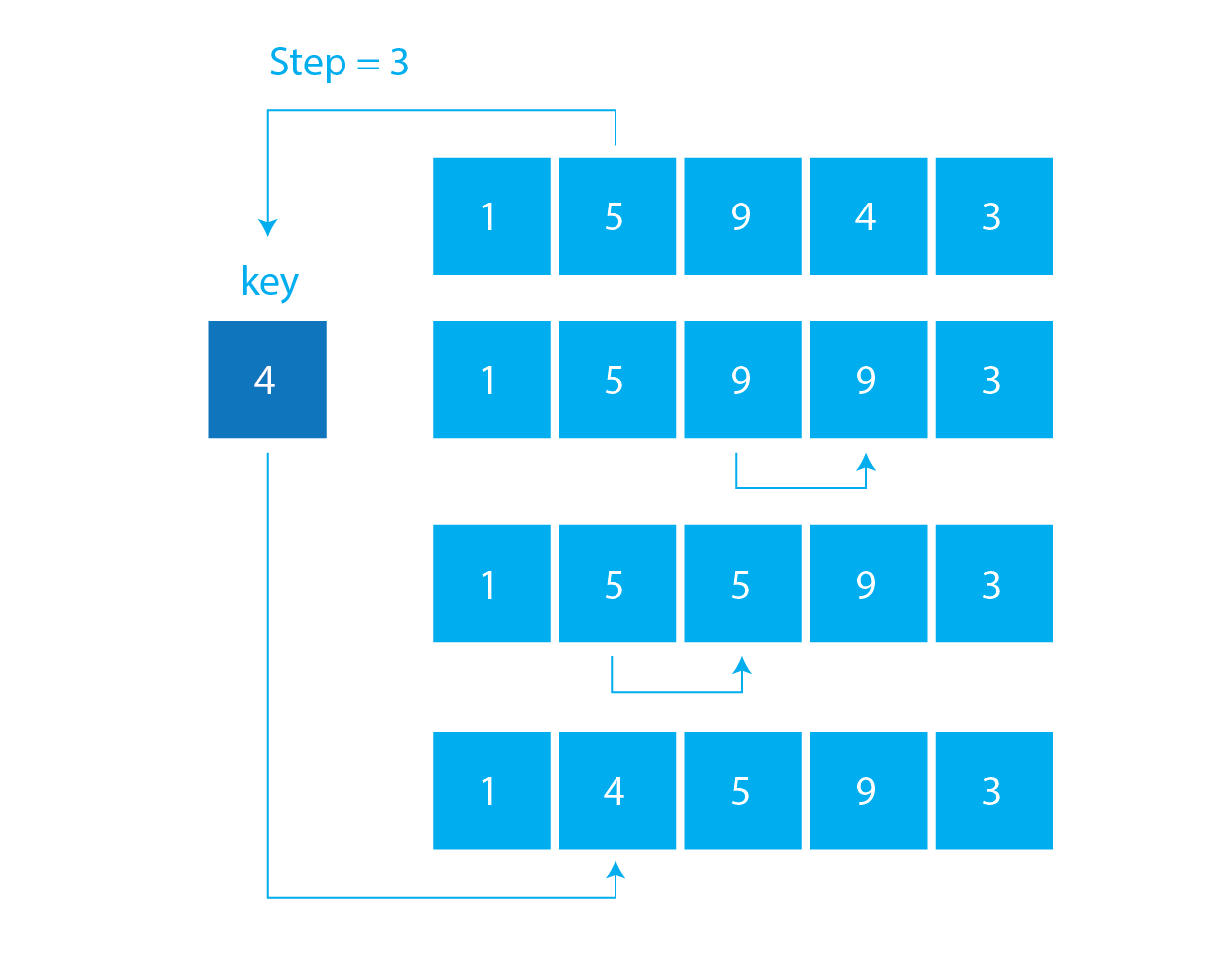
How does Insertion Sort actually Work?

Assume we need to sort the array below.

1. The array’s first element is presumed to be sorted. Take the second element and place it in a separate key. Contrast the key with the first element. If the key is greater than the first element, the key is placed in front of the first element.

   

2. The first two elements have now been sorted. Compare the third element to the elements to the left of it. Place it just behind the smaller element. If there is no element smaller than it, put it at the start of the array.

   

3. Likewise, put each unsorted element in its proper place.

   

   

Pseudo Code of Insertion Sort

procedure insertionSort(arr):
    for i = 1 to n-1
        key = arr[i]
        j = i-1
        while j >= 0 and arr[j] > key
            swap arr[j+1] with arr[j]
            j = j - 1
        end while
    end for
end function

Explanation of Pseudo Code of Insertion Sort
This algorithm sorts an array of items by inserting an element from the unsorted portion of the array into its proper position in the sorted portion of the array on a repeated basis.

1. Only one argument, ‘A,’ a list of sortable items, is accepted by the procedure.
2. The length of the array A is assigned to the variable ‘n’.
3. The outer for loop begins at index ‘1’ and loops for ‘n-1’ iterations, where ‘n’ is the array’s length.
4. The inner while loop begins at the outer for loop’s current index i and compares each element to its left neighbor. The components are switched out if one component is smaller than its left neighbor.
5. The inner while loop moves an element to the left until it is smaller than the element to its left.
6. When the inner while loop is completed, the element at the current index is in its correct position in the array’s sorted portion.
7. The outer for loop iterates through the array until all elements are correctly positioned and the array is completely sorted.

Iterative Approach of Insertion Sort

To sort an array of size N in ascending order, use the following syntax:

1. Iterate through the array from arr[1] to arr[N].
2. Examine the current element (key) in relation to its predecessor.
3. Compare the key element to the elements before it if it is smaller than its predecessor. Move the larger elements up one position to make room for the replaced element.

Java Code of Insertion Sort – Iterative Approach

public class InsertionSort {
    void sort(int arr[])
    {
        int n = arr.length;
        for (int i = 1; i < n; ++i) {
            int key = arr[i];
            int j = i - 1;
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = key;
        }
    }
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i = 0; i < n; ++i)
            System.out.print(arr[i] + " ");

        System.out.println();
    }
    public static void main(String args[])
    {
        int arr[] = { 12, 11, 13, 5, 6 };
        InsertionSort ob = new InsertionSort();
        ob.sort(arr);
        printArray(arr);
    }
}

Output :

5 6 11 12 13

Time Complexity: O(N^2)
Auxiliary Space: O(1)

Recursive Approach of Insertion Sort

1. Traverse the input array from left to right, beginning with the second element.
2. Starting from the rightmost element, compare each element to the elements in the sorted subarray to its left.
3. If an element in the sorted subarray is greater than the current element, it is moved to the right one position.
4. Step 3 should be repeated until you find an element that is less or equal to the current element.
5. Place the current element immediately to the right of the element discovered in step
6. Steps 2–5 must be repeated for all remaining elements in the unsorted subarray.

Java Code of Insertion Sort – Recursive Approach

import java.util.*;
public class Main {
    public static void
    recursiveInsertionSort(ArrayList<Integer> arr, int n)
    {
        if (n <= 1) {
            return;
        }
        recursiveInsertionSort(arr, n - 1);
        int last = arr.get(n - 1);
        int j = n - 2;
        while (j >= 0 && arr.get(j) > last) {
            arr.set(j + 1, arr.get(j));
            j--;
        }
        arr.set(j + 1, last);
    }

    public static void printArray(ArrayList<Integer> arr, int n)
    {
        for (int i = 0; i < n; i++) {
            System.out.print(arr.get(i) + " ");
        }
        System.out.println();
    }

    public static void main(String[] args)
    {
        ArrayList<Integer> arr = new ArrayList<Integer>(
        Arrays.asList(12, 11, 13, 5, 6));
        int n = arr.size();
        recursiveInsertionSort(arr, n);
        printArray(arr, n);
    }
}

Output :

5 6 11 12 13 

Time Complexity
worst case : O(N^2)
best case : O(N)

Space Complexity
O(n) due to the recursion stack.

Conclusion
Insertion sort stands out as a straightforward and effective sorting algorithm, particularly suited for handling small datasets and partially sorted data. It sequentially positions unsorted elements into their correct places within the sorted portion of the array. In Java, insertion sorting can be implemented using either an iterative or recursive method. Although not optimized for large datasets, insertion sort remains valuable for smaller datasets or those that are nearly sorted. For larger datasets, alternative algorithms like merge sort or quicksort may be more appropriate.

Frequently Asked Questions (FAQs) Related to Insertion Sort in Java

Below are some of the FAQs related to Insertion Sort in Java:

1. How does insertion sort work?
Insertion sort works by iterating over the array starting from the second element. For each element, it compares it with the elements before it and moves them to the right until it finds the correct position for the current element.

2. What is the time complexity of insertion sort?
The time complexity of insertion sort is O(n^2) in the worst-case scenario, where n is the number of elements in the array. However, it has an average-case time complexity of O(n^2) and a best-case time complexity of O(n) for nearly sorted arrays.

3. Is insertion sort stable?
Yes, insertion sort is a stable sorting algorithm. This means that it preserves the relative order of equal elements in the sorted array.

4. When should I use insertion sort?
Insertion sort is suitable for sorting small arrays or nearly sorted arrays. It is also a good choice when the input array is almost sorted or when the memory space is limited, as it has a small memory footprint compared to other sorting algorithms.

5. Can insertion sort be used for sorting linked lists?
Yes, insertion sort can be used for sorting linked lists. It works by repeatedly inserting the next element into its correct position in the sorted sublist, similar to how it works for arrays.