Last Updated on May 11, 2023 by Prepbytes

In this article, we’ll look at how to reverse a queue. We must reverse a queue with only standard operations:
- enqueue(element): Add an element to the queue’s tail.
- dequeue(): Removes an element from the queue’s front end.
- empty(): Returns true if the queue is empty, otherwise false.
Before we get there, let’s go over some fundamental queue data structure concepts.
What is a Queue?
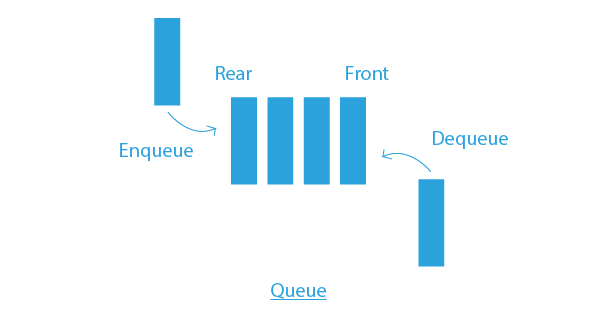
Queue follows the principle of FIFO (First in First out) i.e. element which is inserted first will be removed first. The operation for insertion of elements is known as enqueue operation and the operation for deletion of elements is known as dequeue operation. Like Stack, Queue is also a linear data structure.
Examples:
Input 1:
Queue = [11, 22, 33, 44, 55]Output 1:
Queue = [55, 44, 33, 22, 11]Input 2:
Queue = [12, 24, 36, 48]Output 2:
Queue = [48, 36, 24, 12]Approach 1: Reverse a Queue
One method for reversing the queue is to store the queue elements in a stack so that when we re-insert the queue elements, they are inserted in reverse order. We use stack because it has the ‘LIFO’ property, which means that the last element inserted into the data structure should be the first element of the reversed queue. This problem is solved using a stack. It will be a two-step process:
- Push an element from the front end of the queue into the stack. (The stack’s top element will be the queue’s last element.)
- Push an element from the top of the stack to the back of the queue. (The last element of the stack will be the first to be inserted into the queue.)
Code Implementation
#include <bits/stdc++.h>
using namespace std;
void Print(queue<int>& Queue)
{
while (!Queue.empty()) {
cout << Queue.front() << " ";
Queue.pop();
}
}
void reverseQueue(queue<int>& Queue)
{
stack<int> Stack;
while (!Queue.empty()) {
Stack.push(Queue.front());
Queue.pop();
}
while (!Stack.empty()) {
Queue.push(Stack.top());
Stack.pop();
}
}
int main()
{
queue<int> Queue;
Queue.push(10);
Queue.push(20);
Queue.push(30);
Queue.push(40);
Queue.push(50);
Queue.push(60);
Queue.push(70);
Queue.push(80);
Queue.push(90);
Queue.push(100);
reverseQueue(Queue);
Print(Queue);
}
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class Queue_reverse {
static Queue<Integer> queue;
static void Print()
{
while (!queue.isEmpty()) {
System.out.print(queue.peek() + ", ");
queue.remove();
}
}
static void reversequeue()
{
Stack<Integer> stack = new Stack<>();
while (!queue.isEmpty()) {
stack.add(queue.peek());
queue.remove();
}
while (!stack.isEmpty()) {
queue.add(stack.peek());
stack.pop();
}
}
public static void main(String args[])
{
queue = new LinkedList<Integer>();
queue.add(10);
queue.add(20);
queue.add(30);
queue.add(40);
queue.add(50);
queue.add(60);
queue.add(70);
queue.add(80);
queue.add(90);
queue.add(100);
reversequeue();
Print();
}
}
from queue import Queue
def Print(queue):
while (not queue.empty()):
print(queue.queue[0], end=", ")
queue.get()
def reversequeue(queue):
Stack = []
while (not queue.empty()):
Stack.append(queue.queue[0])
queue.get()
while (len(Stack) != 0):
queue.put(Stack[-1])
Stack.pop()
if __name__ == '__main__':
queue = Queue()
queue.put(10)
queue.put(20)
queue.put(30)
queue.put(40)
queue.put(50)
queue.put(60)
queue.put(70)
queue.put(80)
queue.put(90)
queue.put(100)
reversequeue(queue)
Print(queue)
Complexity Analysis to Reverse a Queue Using a Stack
Time Complexity: The time complexity of this approach is O(n) as we need to insert all the elements in the stack and then add them to the queue.
Space Complexity: The space complexity of this approach is O(n) as we use the stack to store all the elements of the queue.
Approach 2: Reverse a Queue Using Recursion
For reversing the queue, we will use the concept of recursion. The approach will first remove the front element from the queue and recursively call the reverse function for the remaining queue. By following this, we are dividing the larger problem into smaller sub-problems.
Recursive Algorithm
- Pop an element from the queue if the queue has elements; otherwise, return an empty queue.
- Call the revQueue function for the remaining queue.
- At last, push the popped element into the resultant reversed queue.
Pseudo Code
queue revQueue(queue)
{
if (queue is empty)
return queue;
else {
data = queue.front()
queue.pop()
queue = revQueue(queue);
q.push(data);
return queue;
}
}Code Implementation
#includeusing namespace std; void printQueue(queue Queue) { while (!Queue.empty()) { cout << Queue.front() << " "; Queue.pop(); } } void revQueue(queue & q) { if (q.empty()) return; long long int data = q.front(); q.pop(); revQueue(q); q.push(data); } int main() { queue Queue; Queue.push(1); Queue.push(2); Queue.push(3); Queue.push(4); Queue.push(5); revQueue(Queue); printQueue(Queue); }
// Java program to reverse a Queue by recursion
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
// Java program to reverse a queue recursively
class Queue_reverse {
static Queue queue;
// Utility function to print the queue
static void Print()
{
while (!queue.isEmpty())
{
System.out.print(queue.peek() + " ");
queue.remove();
}
}
// Recurrsive function to reverse the queue
static Queue revQueue(Queue q)
{
// Base case
if (q.isEmpty())
return q;
// Dequeue current item (from front)
int data = q.peek();
q.remove();
// Reverse remaining queue
q = revQueue(q);
// Enqueue current item (to rear)
q.add(data);
return q;
}
// Driver code
public static void main(String args[])
{
queue = new LinkedList();
queue.add(1);
queue.add(2);
queue.add(3);
queue.add(4);
queue.add(5);
queue = revQueue(queue);
Print();
}
}
from queue import Queue
def revQueue(queue: Queue):
if queue.empty():
return
item = queue.queue[0]
queue.get()
revQueue(queue)
queue.put(item)
def print_queue(queue: Queue):
while not queue.empty():
print(queue.queue[0], end=" ")
queue.get()
print()
if __name__ == "__main__":
q = Queue()
q.put(1)
q.put(2)
q.put(3)
q.put(4)
q.put(5)
revQueue(q)
print_queue(q)
Complexity Analysis to Reverse a Queue Using Recursion
Time Complexity: The time complexity of using a recursive function to reverse a queue is O(n).
Space Complexity: Because recursive functions use stack internally, the auxiliary space for reversing a queue using a recursive function will be O(n).
Conclusion
The article goes over two methods for reversing a queue with standard queue operations. The first method employs a stack to store queue elements in reverse order, while the second employs recursion to divide the problem into smaller sub-problems. Both approaches have an O(n) time complexity and an O(n) space complexity due to the use of auxiliary space for storing elements in the stack or the internal stack used in the recursive function.
Frequently Asked Questions (FAQs)
Q1. In C++, is it possible to reverse a queue?
Ans. A queue is a popular First in First Out linear user-defined data structure that can be reversed because it is a linear data structure.
Q2. How long does it take to reverse a queue?
Ans. So, in this approach to reversing a queue, we will dequeue all of the queue’s elements and push them into the stack, and then, once the queue is empty, we will pop elements from the stack and insert them into the queue. Time Complexity: O(n), where n is the queue size and we iterate the queue once.
Q3. How do I reverse a two-queue queue?
Ans. Assume q1 contains 1,2,3,4,5 elements, which we will reverse and add to q2 as 5,4,3,2,1. Algorithm: There are two queues, q1 and q2. Add the elements to q1, then iterate until size-2 of q1 and add these elements to the back end of q1, resulting in the last element in the first position.
Q4. What is the complexity of a queue’s space?
Ans. Because no extra space is required for any operation, the space complexity for each operation in a queue is O(1).


