Sum Query

Last Updated on March 31, 2022 by Ria Pathak

Concepts Used

Segment Trees

Difficulty Level

Easy

Problem Statement :

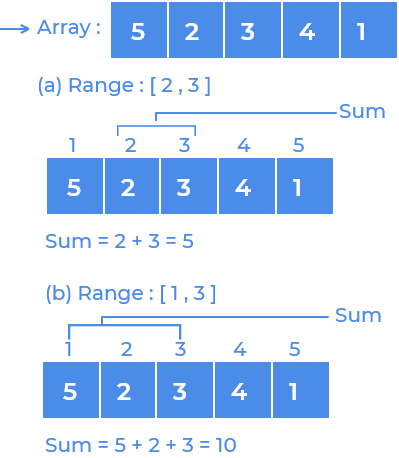
Given an array of N elements and Q queries. In each query he is given two values l,r.
We have to find the sum of all the elements from l to r. As the sum might be quite large print the answer modulo 10^9+7.

See original problem statement here

Solution Approach :

Introduction :

Idea is to construct a segment tree with the leaf nodes having the array values and intermediate nodes stores the sum of the current subarray range.
For Example : arr {5,1,4,2,9} is our array then segment tree will store values like this -> {5,1,4,2,9}->21 , {5,1,4}-> 10, {5,1}-> 6, {5}-> 5(leaf), {1}->1 (leaf), {2,9}->11, {2}->2(leaf), {9}->9 (leaf).

Method 1 (Brute force):

We can sum up the values in the given range l to r for every query. This approach will work fine for smaller array sizes and queries, as it takes linear time to find sum for the of the values for single query. As the size of the input increases this apprach will be huge drawback.

Method 2 (Segment Tree):

As the number of queries and array size is too large for linear search in every query, we will use segment tree to solve this problem.
A Segment Tree is a data structure which allows answering range queries very effectively over a large input. Each query takes logarithmic time. Range queries includes sum over a range, or finding a minimum value over a given range etc. Query be of any type we can use segment trees and modify it accordingly.
Leaf nodes of the tree stores the actual array values and intermediate nodes stores the information of subarrays with is require to solve the problem. Lets say if we have to find a sum between different ranges, so now the intermediate nodes will store the sum of the current subarray. We fill the nodes by recursively calling left and right subtree (dividing into segements), untill there is a single element left, which can be directly assigned the value of the array. Array representation of the tree is used to represent segment tree, where (i*2)+1 represents the left node and (i*2)+2 represents right node, parent will be represented by (i-1)/2 for every index i.
We will construct our tree by starting at the original array and dividing it into two halves (left and right), untill there is a single element left (leaf) which can directly be filled with a[i] for any index i. Now for every range say l to r, we will store the sum of the current range in the node.
Now that our tree is constructed, we will answer queries (sum of the given range). The queries can be of 3 types:

1. The range of the tree exactly matches with the query, in this case we will return the value stored in this node.
2. The range either belongs to the left or right node, in this case we will make two recursive calls for left and right subtrees respectively.
3. The range overlaps with two of more ranges, in this case we are forced to go to the lower levels of both subtrees and find the sum of the range which fits the range and finally sum up the values returned by both subtrees.

Algorithm :

construct():

• if the current node is a leaf (subarray contains single element), assign the value directly, (tree[curr]= arr[l]).
• break the tree into two halves by recursively calling for left and right subtree, construct(l,mid) and construct(mid+1,r)
• fill the current node with the sum of left & right node. (tree[curr] = LeftSubtree + RightSubtree).

RMQ():

• if range is within the current range, return the value stored in node.
• if left range is greater than right range, return 0.
• else return the sum of left & right subtrees.

Complexity Analysis :

In segment tree, preprocessing time is O(n) and worst time to for range minimum query is equivalent to the height of the tree.
The space complexity is O(n) to store the segment tree.

Solutions:

#include <stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>

int getMid(int s, int e) { return s + (e -s)/2; } 

int getSumUtil(int *st, int ss, int se, int qs, int qe, int si) 
{ 

    if (qs <= ss && qe >= se) 
        return st[si]; 
    if (se < qs || ss > qe) 
        return 0; 

    int mid = getMid(ss, se); 
    return getSumUtil(st, ss, mid, qs, qe, 2*si+1) + 
        getSumUtil(st, mid+1, se, qs, qe, 2*si+2); 
} 

int getSum(int *st, int n, int qs, int qe) 
{ 
    // Check for erroneous input values 
    if (qs < 0 || qe > n-1 || qs > qe) 
    { 

        return -1; 
    } 

    return getSumUtil(st, 0, n-1, qs, qe, 0); 
} 


int constructSTUtil(int arr[], int ss, int se, int *st, int si) 
{ 

    if (ss == se) 
    { 
        st[si] = arr[ss]; 
        return arr[ss]; 
    } 

    int mid = getMid(ss, se); 
    st[si] = constructSTUtil(arr, ss, mid, st, si*2+1) + 
            constructSTUtil(arr, mid+1, se, st, si*2+2); 
    return st[si]; 
} 

int *constructST(int arr[], int n) 
{ 

    int x = (int)(ceil(log2(n))); 

    int max_size = 2*(int)pow(2, x) - 1; 
    int *st = (int *)malloc(sizeof(int)*max_size);

    constructSTUtil(arr, 0, n-1, st, 0); 

    return st; 
} 

int main() 
{ 
  int t;
  scanf("%d",&t);
  while(t--)
  {
    int n;
    scanf("%d",&n);
      int arr[n] ; 
      for(int i=0;i<n;i++)
       scanf("%d",&arr[i]);

      int *st = constructST(arr, n); 
      int q;
      scanf("%d",&q);
      while(q--)
      {

      int l,r;
      scanf("%d %d",&l,&r);
      l-=1;
      r-=1;
      printf("%d\n",getSum(st, n, l,r)); 

      }
  }
    return 0; 
} 

#include <bits/stdc++.h> 
using namespace std; 

int getMid(int s, int e) { return s + (e -s)/2; } 

int getSumUtil(int *st, int ss, int se, int qs, int qe, int si) 
{ 

    if (qs <= ss && qe >= se) 
        return st[si]; 

    if (se < qs || ss > qe) 
        return 0; 

    int mid = getMid(ss, se); 
    return getSumUtil(st, ss, mid, qs, qe, 2*si+1) + 
        getSumUtil(st, mid+1, se, qs, qe, 2*si+2); 
} 

int getSum(int *st, int n, int qs, int qe) 
{ 

    if (qs < 0 || qe > n-1 || qs > qe) 
    { 
        return -1; 
    } 

    return getSumUtil(st, 0, n-1, qs, qe, 0); 
} 


int constructSTUtil(int arr[], int ss, int se, int *st, int si) 
{ 

    if (ss == se) 
    { 
        st[si] = arr[ss]; 
        return arr[ss]; 
    } 

    int mid = getMid(ss, se); 
    st[si] = constructSTUtil(arr, ss, mid, st, si*2+1) + 
            constructSTUtil(arr, mid+1, se, st, si*2+2); 
    return st[si]; 
} 

int *constructST(int arr[], int n) 
{ 

    int x = (int)(ceil(log2(n))); 

    int max_size = 2*(int)pow(2, x) - 1; 

    int *st = new int[max_size]; 

    constructSTUtil(arr, 0, n-1, st, 0); 

    return st; 
} 

int main() 
{ 
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    cin>>n;
      int arr[n] ; 
      for(int i=0;i<n;i++)
       cin>>arr[i];

      int *st = constructST(arr, n); 
      int q;
      cin>>q;
      while(q--)
      {

      int l,r;
      cin>>l>>r;
      l-=1;
      r-=1;
      cout<<getSum(st, n, l,r)<<endl; 

      }
  }
    return 0; 
} 

import java.util.*;
class Main
{ 
    int st[]; // The array that stores segment tree nodes 
   Main(int arr[], int n) 
    { 

        int x = (int) (Math.ceil(Math.log(n) / Math.log(2))); 

        //Maximum size of segment tree 
        int max_size = 2 * (int) Math.pow(2, x) - 1; 

        st = new int[max_size]; // Memory allocation 

        constructSTUtil(arr, 0, n - 1, 0); 
    } 

    int getMid(int s, int e) { 
        return s + (e - s) / 2; 
    } 

    int getSumUtil(int ss, int se, int qs, int qe, int si) 
    { 

        if (qs <= ss && qe >= se) 
            return st[si]; 

        if (se < qs || ss > qe) 
            return 0; 

        int mid = getMid(ss, se); 
        return getSumUtil(ss, mid, qs, qe, 2 * si + 1) + 
                getSumUtil(mid + 1, se, qs, qe, 2 * si + 2); 
    } 


    int getSum(int n, int qs, int qe) 
    { 
        // Check for erroneous input values 
        if (qs < 0 || qe > n - 1 || qs > qe) { 
            System.out.println("Invalid Input"); 
            return -1; 
        } 
        return getSumUtil(0, n - 1, qs, qe, 0); 
    } 

    int constructSTUtil(int arr[], int ss, int se, int si) 
    { 

        if (ss == se) { 
            st[si] = arr[ss]; 
            return arr[ss]; 
        } 


        int mid = getMid(ss, se); 
        st[si] = constructSTUtil(arr, ss, mid, si * 2 + 1) + 
                constructSTUtil(arr, mid + 1, se, si * 2 + 2); 
        return st[si]; 
    } 


    public static void main(String args[]) 
    { 
      Scanner sc = new Scanner(System.in);
      int t= sc.nextInt();
      while(t-->0)
      {
        int n = sc.nextInt();



          int []arr = new int[n];
          for(int i=0;i<n;i++)
           arr[i] = sc.nextInt();

          Main tree = new Main(arr, n); 
          int q = sc.nextInt();
          while(q-->0)
          {

          int l = sc.nextInt()-1;
          int r = sc.nextInt()-1;

            System.out.println(tree.getSum(n, l,r)); 
          }

      }
    } 
} 

[forminator_quiz id="2305"]

This article tried to discuss Segment Trees. Hope this blog helps you understand and solve the problem. To practice more problems on Segment Trees you can check out MYCODE | Competitive Programming.