Last Updated on July 21, 2023 by Mayank Dham

In this article, we will delve deep into the topic of finding the greatest common divisor, GCD of two numbers. Understanding how to find the GCD of two numbers not only improves your fundamental logical and coding skills but also enhances your career prospects. Regular practice with coding questions, such as determining the GCD of two numbers, is an excellent habit that prepares you for technical interviews with various organizations. Additionally, the GCD is a key concept used to solve many complex problems. Whether you are just starting out in coding or are already on a coding career path, grasping the basics of finding the GCD of two numbers is essential. Let’s now proceed to explore and solve the problem of finding the GCD of two numbers.
How to Find GCD of Two Numbers:
For given two large numbers M and N, find their gcd(M,N).
GCD(M,N) is the largest number possible which divides both.
Finding a GCD of two numbers is not a complicated task. From basic mathematics you can solve how to find GCD of two numbers.
See original problem statement here
Test Case:
Input: 15 130
Output: 5
Explanation:
5 divides 15 and 130 both completely and there exists no number greater than 5 which divides both of them completely.
Solving Approach How To Find GCD Of Two Numbers :
- For provided numbers, we know N is of size less than or equal to 100, so we would need to store this number in a string.
- We know we get the remainder less than N always if we divide any number by N.
- To get the remainder by dividing a number stored String by Number, we calculate the remainder digit by digit. We update the remainder at every digit until all strings are iterated.
- In each iteration, we take the digit and make it greater than our current remainder by multiplying it by 10 and adding it to the digit, now we take the mod of digit by N and store it as our current remainder. After the whole string is iterated, we get our remainder.
- After we divide M by N and extract it’s remainder, now both of them are in the Long Integer range, and we can carry with us our Long Division Method for getting gcd(M,N) where M is our new smaller number.
- Long Division Method: We repeatedly store remainder i.e (Larger number % Smaller number) and update Larger number by Smaller number until smaller number completely divides the larger number. Last Smaller Number after all steps, is our gcd.
Example:
We’ll be given two numbers out of which one is a string and one is a long number. Hence we find the remainder of string number and long number.
We can dry run the above mentioned technique,let’s say given numbers are 143254 and 3, so first we convert 143254 to a long number which will be 143254 % 3. We take mod=0, which will store our final value, So,

As we have got our values in integer form, we can now use the long division method, to find out the gcd of both numbers that is gcd(n,mod).
Let’s take 25 and 135 for example, we find gcd of both using the Long Division Method.
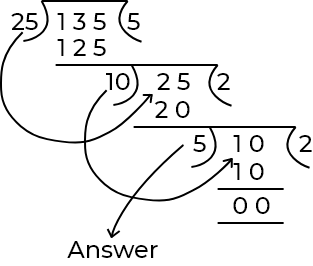
As soon as our remainder becomes 0, dividend is our gcd(a,b). Let’s see all the solutions for finding gcd of two numbers in (c, java, Python).
Solutions:
#include <stdio.h>
#include<string.h>
long long modBigNumber(char num[], long long m)
{
long long mod = 0;
for (int i = 0; i < strlen(num); i++) {
int digit = num[i] - '0';
mod = mod * 10 + digit;
mod = mod % m;
}
return mod;
}
int main()
{
int test;
scanf("%d",&test);
while(test--){
long long small;
long long largeF;
char large[2001];
scanf("%lld%s",&small,large);
largeF = modBigNumber(large,small);
if(largeF==0){
printf("%lld\n",small);
}
else{
int temp = small;
small = largeF;
largeF = temp;
while(1){
if(largeF%small==0){
printf("%lld\n",small);
break;
}
int temp = small;
small = largeF%small;
largeF = temp;
}
}
}
}
#include <bits/stdc++.h>
using namespace std;
long long modBigNumber(string num, long long m)
{
long long mod = 0;
for (int i = 0; i < num.size(); i++) {
int digit = num[i] - '0';
mod = mod * 10 + digit;
mod = mod % m;
}
return mod;
}
int main()
{
int test;
cin>>test;
while(test--){
long long small;
long long largeF;
string large;
cin>>small>>large;
largeF = modBigNumber(large,small);
if(largeF==0){
cout<<small<<endl;
}
else{
int temp = small;
small = largeF;
largeF = temp;
while(true){
if(largeF%small==0){
cout<<small<<endl;
break;
}
int temp = small;
small = largeF%small;
largeF = temp;
}
}
}
}
import java.util.*;
import java.io.*;
public class Main {
static long modBigNumber(String num, long m){
long mod = 0;
for (int i = 0; i < num.length(); i++) {
int digit = num.charAt(i) - '0';
mod = mod * 10 + digit;
mod = mod % m;
}
return mod;
}
public static void main(String args[]) throws IOException {
Scanner sc = new Scanner(System.in);
int test = sc.nextInt();
while(test!=0){
long small = sc.nextLong();
long largeF;
String large = sc.next();
largeF = modBigNumber(large,small);
if(largeF==0){
System.out.println(small);
}
else{
long temp = small;
small = largeF;
largeF = temp;
while(true){
if(largeF%small==0){
System.out.println(small);
break;
}
temp = small;
small = largeF%small;
largeF = temp;
}
}
test--;
}
}
}
Conclusion
In conclusion, we have explored various methods to find the greatest common divisor (GCD) of two numbers. Understanding how to calculate the GCD is an essential skill that improves your logical thinking and problem-solving capabilities. It is a fundamental concept used in many complex coding problems and can significantly contribute to your success in technical interviews and competitive programming. Whether you are starting your coding journey or already pursuing a coding career, mastering the GCD computation will undoubtedly strengthen your skills and make you a more proficient coder.
Frequently Asked Questions (FAQs) related to GCD of two numbers
Some FAQs related to GCD of two numbers:
Q1. Why is finding the GCD important in programming?
Finding the GCD is crucial in programming because it is used in various algorithms and mathematical computations. It helps in simplifying fractions, solving modular arithmetic problems, and optimizing algorithms like the Euclidean algorithm.
Q2. What are the different methods to find the GCD of two numbers?
There are several methods to find the GCD of two numbers, including the Euclidean algorithm, backtracking, prime factorization, and binary GCD algorithm. Each method has its advantages and may be suitable for different scenarios.
Q3. Can the GCD of two numbers be larger than the numbers themselves?
No, the GCD of two numbers can never be larger than the numbers themselves. The GCD will always be less than or equal to the smaller of the two numbers.
Q4. How does the Euclidean algorithm work for finding the GCD?
The Euclidean algorithm uses repeated division to find the GCD of two numbers. It continuously divides the larger number by the smaller number and assigns the remainder as the new dividend until the remainder becomes zero. The GCD is then the last non-zero remainder obtained in the process.
Q5. Is the GCD of two numbers unique?
Yes, the GCD of two numbers is unique and remains the same regardless of the order of the two numbers.
Q6. Can the GCD of two numbers be negative?
The GCD is defined as a positive integer, so it is always non-negative. However, if one or both of the input numbers are negative, the absolute values are used to calculate the GCD.


