Last Updated on November 18, 2022 by Sumit Kumar

Given an undirected graph and M colors, the problem is to find if it is possible to color the graph with at most M colors or not.
See original problem statement here
How to Solve M Coloring Problem :
Idea is to assign different colors (1-M) to all the adjacent vertices. If at any point the color of any two adjacent vertices are same then we say it is not possible, otherwise it is.
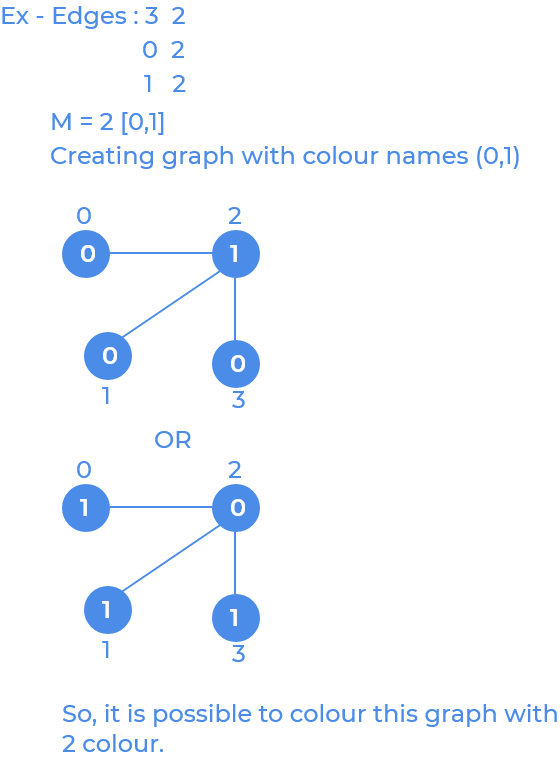
How backtracking Help:
We will use backtracking to solve the above problem.
Backtracking is the approach to solve the problem by testing all possible combinations. If any subproblem does not fit the given constraint then we discard the complete subproblem (backtrack), moves a step back then try other remaining possible combinations. Backtracking algorithm is generally exponential in time.
We will take a color array color[] to store M colours. Now iterate through color[] , then we will assign each colour to all vertices one-by-one. If any colour assignment does not match the constraints then we will backtrack and unassign the colour which has been assigned to the vertex earlier. If the vertex count reaches the total number of vertices we will return true, and if none of the assignment matches the given condition (adjacent vertices must have different colours) then we will return false.
Algorithm to Solve M Coloring Problem:
colour():
- If
index == number.of.vertices, return TRUE. - else, for every
k= 1toM:- assign color to the current vertex,
v, (color[v]=k) - if colour(graph,vertex+1,color)==TRUE, return true
- else ,
- mark the colour as unassigned, (
colour[v]=0) (backtracking step). - If none of the combination satisfies, return FALSE.
- assign color to the current vertex,
Complexity Analysis :
In this method each vertex has M different choices of colors. So the total time complexity is MV , where M is the number of colours and V is the number of vertices.
Program to Solve M Coloring Problem:
#include <stdio.h>
int V;
int isSafe(int v, int graph[V][V],int color[], int c)
{
for (int i = 0; i < V; i++)
if (
graph[v][i] && c == color[i])
return 0;
return 1;
}
int colour(int graph[V][V], int m,int color[], int v)
{
if (v == V)
return 1;
for (int c = 1; c <= m; c++)
{
if (isSafe(
v, graph, color, c)) {
color[v] = c;
if ( colour(graph, m, color, v + 1)== 1)
return 1;
color[v] = 0;
}
}
return 0;
}
int graphColoring(int graph[V][V], int m)
{
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (
colour(graph, m, color, 0)== 0) {
return 0;
}
return 1;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int e;
scanf("%d %d",&V,&e);
int graph[V][V];
for(int i=0;i<V;i++)
{
for(int j=0;j<V;j++)
graph[i][j]=0;
}
while(e--)
{
int u,v;
scanf("%d %d",&u,&v);
graph[u][v]=1;
graph[v][u]=1;
}
int m; // Number of colors
scanf("%d",&m);
printf("%d\n",graphColoring(graph, m));
}
return 0;
}
#include<iostream>
#define V 100
using namespace std;
int isSafe(int v, int graph[V][V],int color[], int c)
{
for (int i = 0; i < V; i++)
if (
graph[v][i] && c == color[i])
return 0;
return 1;
}
int colour(int graph[V][V], int m,int color[], int v)
{
if (v == V)
return 1;
for (int c = 1; c <= m; c++)
{
if (isSafe(
v, graph, color, c)) {
color[v] = c;
if ( colour(graph, m, color, v + 1)== 1)
return 1;
color[v] = 0;
}
}
return 0;
}
int graphColoring(int graph[V][V], int m)
{
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (
colour(graph, m, color, 0)== 0) {
return 0;
}
return 1;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n,e;
cin>>n>>e;
int graph[V][V];
for(int i=0;i<V;i++)
{
for(int j=0;j<V;j++)
graph[i][j]=0;
}
while(e--)
{
int u,v;
cin>>u>>v;
graph[u][v]=1;
graph[v][u]=1;
}
int m; // Number of colors
cin>>m;
cout<<graphColoring(graph, m)<<endl;
}
return 0;
}
import java.util.*;
import java.io.*;
public class Main{
final int V = 100;
int color[];
boolean isSafe(
int v, int graph[][], int color[],
int c)
{
for (int i = 0; i < V; i++)
if (
graph[v][i] == 1 && c == color[i])
return false;
return true;
}
boolean graphColoringUtil( int graph[][], int m,int color[], int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (
graphColoringUtil(
graph, m,
color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
boolean graphColoring(int graph[][], int m)
{
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (
!graphColoringUtil(
graph, m, color, 0)) {
return false;
}
return true;
}
public static void main(String args[])
{
Main m = new Main();
Scanner sc= new Scanner(System.in);
int t = sc.nextInt();
while(t-->0)
{
int n = sc.nextInt();
int e = sc.nextInt();
int [][]graph = new int [m.V][m.V];
for(int i=0;i<m.V;i++)
{
for(int j = 0; j<m.V;j++)
{
graph[i][j]=0;
}
}
while(e-->0)
{
int u = sc.nextInt();
int v = sc.nextInt();
graph[u][v]=1;
graph[v][u]=1;
}
int no = sc.nextInt();
if(m.graphColoring(graph, no)==false)
System.out.println("0");
else
System.out.println("1");
}
}
}
V = 100 def isSafe(v, graph, color, c): V = 100 for i in range(V): if (graph[v][i] and c == color[i]): return 0 return 1 def colour( graph, m, color, v): if (v == V): return 1 for c in range(1, m + 1): if (isSafe(v, graph, color, c)): color[v] = c if ( colour(graph, m, color, v + 1)== 1): return 1 color[v] = 0 return 0 def graphColoring( graph, m): V = 100 color = [0] * V for i in range(V): color[i] = 0 if (colour(graph, m, color, 0)== 0): return 0 return 1 for _ in range(int(input())): n, e = map(int,input().split()) graph = [[0 for i in range(100)] for j in range(100)] while e: e -= 1 u, v = map(int,input().split()) graph[u][v] = 1 graph[v][u] = 1 m = int(input()) print(graphColoring(graph, m))
[forminator_quiz id="2077"]
This article tried to discuss the concept of Backtracking. Hope this blog helps you understand and solve the problem. To practice more problems you can check out MYCODE | Competitive Programming


