FOOLISH ITEMS

Last Updated on March 30, 2022 by Ria Pathak

CONCEPTS USED:

Dynamic programming.

DIFFICULTY LEVEL:

Easy.

PROBLEM STATEMENT(SIMPLIFIED):

Arnab is now handed N rupees, he is asked by his mom to buy at least two ingredients which when used to make a dish will be sweetest.
The sweetness of the dish is the product of the cost of all the ingredients.
Now Arnab’s Mom has given Arnab the exact amount, so after buying the suitable ingredients there will be no money left with Arnab. The market which Arnab visits have ingredients of all possible positive costs (cost>0). Help Arnab find the maximum value of sweetness.

For Example :

N=4,

4 can be divided into (1,3)and (2,2) . (2,2) gives the maximum result i.e. 4.

N=5,

Similarly,we can divide 5 as- (1,4) and (2,3). 2*3 gives the maximum product.

OBSERVATION:

WRONG APPROACH:

One may think that dividing the given number into two equal halves gives the maximum product. But this approach is wrong.

Example: N=10; if you think (5,5) gives the maximum product ,you are wrong because the maximum product is 36!!
10 can be divided as [3,3,4].

Mathematically, we are given n and we need to maximize a1 a2 a3 …. * aK such that n = a1 + a2 + a3 … + aK and a1, a2, … ak > 0.

SOLVING APPROACH:

This problem is similar to Rod Cutting Problem. We can get the maximum product by making a cut at different positions and comparing the values obtained after a cut. We can recursively call the same function for a piece obtained after a cut.

Can you think of the recursive function now?

maxProduct(n) = max(i(n-i), maxProductRec(n-i)i)

for all i in {1, 2, 3 .. n},where maxProduct(n) is the maximum product of divisions of n.
Refer to this image for better understanding.

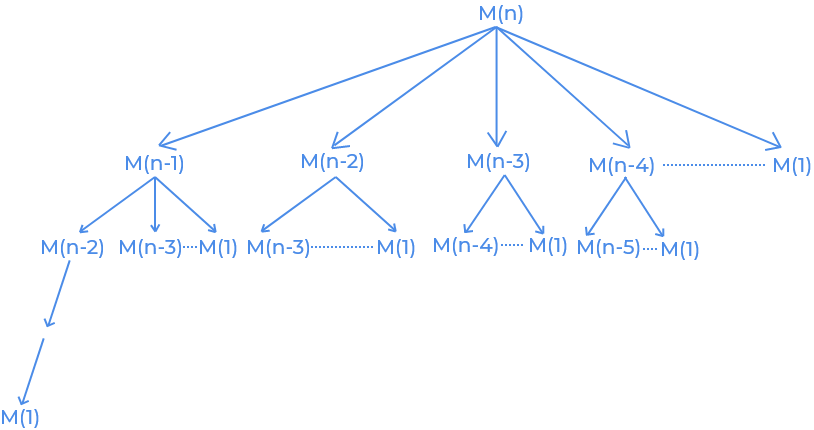
You are encouraged to implement the above brute force on your own first ,before looking at the solution.
See original problem statement here

Overlapping Subproblems:

Let’s consider the conditions for using DP to find an efficient solution:
Overlapping Sub-problems — Yes. From the image above ,you can notice the overlapping subproblems. When you implement using recursion, each subproblem will be computed several times.
Optimal Substructure — Yes. At each node in the call-tree, we’re calling the recursive function on a smaller number. The decision which path to go down is based on the max product returned for each sub-problem.

Recomputations of same subproblems can be avoided by constructing a temporary array dp[] in bottom up manner.

O(n) approach:

The idea is to break the number into multiples of 2 or 3. If you write the breaking results for couple of numbers like 7 to 10 you should get the idea. Assuming the max number is 60, there is a simple dynamic solution:

int dp[60];
public:
int integerBreak(int n)
{
dp[1]=1,dp[2]=1,dp[3]=2,dp[4]=4,dp[5]=6,dp[6]=9;
for(int i=7;i<=n;i++)
dp[i]=max(dp[i-3]*3,dp[i-2]*2);
return dp[n];
}

SOLUTIONS:

 #include <stdio.h>
     int main()
     {
     //write your code here
      long long int dp[101];
     dp[1]=0,dp[2]=1,dp[3]=2,dp[4]=4,dp[0]=0,dp[5]=6,dp[6]=9;
     for(int i=7;i<101;i++)
     {long long int mx=-1;
     for(int j=1;j<=i;j++)
     {
      mx=mx>dp[j]*(i-j)?mx:dp[j]*(i-j);
     }dp[i]=mx;
     }
      int t;scanf("%d",&t);
      while(t--)
     {
     int n;scanf("%d",&n);
     printf("%d\n",dp[n]);
     }
     return 0;
      }

#include <bits/stdc++.h>
      using namespace std;

      int main()
      {
      //write your code here
     long long int dp[101];
     dp[1]=0,dp[2]=1,dp[3]=2,dp[4]=4,dp[0]=0,dp[5]=6,dp[6]=9;
    for(int i=7;i<101;i++)
     {long long int mx=-1;
     for(int j=1;j<=i;j++)
     {
      mx=max(mx,dp[j]*(i-j));
     }dp[i]=mx;
     }
     int t;cin>>t;
     while(t--)
     {
    int n;cin>>n;
    cout<<dp[n]<<"\n";
     }
     return 0;
     }

    import java.util.Scanner;
     import java.util.*;

      class HelloWorld{
     public static void main(String []args){
        Scanner myObj = new Scanner(System.in);
        long [] dp = new long[101];
        dp[1]=0;dp[2]=1;dp[3]=2;dp[4]=4;dp[0]=0;dp[5]=6;dp[6]=9;

        for(int i=7;i<101;i++){
        long mx=-1;
             for(int j=1;j<=i;j++){
                  mx=Math.max(mx,dp[j]*(i-j));
             }
             dp[i]=mx;
        }
        int t=myObj.nextInt();
        while(t-- > 0){
            int n=myObj.nextInt();
            System.out.println(dp[n]);
        }
     }
     }

dp = [0 for i in range(101)]
dp[1] = 0
dp[2] = 1
dp[3] = 2
dp[4] = 4
dp[0] = 0
dp[5] = 6
dp[6] = 9
for i in range(7, 101):
	
	mx = -1
	
	for j in range(1, i + 1):
	
		if mx > dp[j] * (i - j):
			mx = mx
	
		else:
			mx = dp[j] * (i - j)
	
		dp[i] = mx
	
for _ in range(int(input())):
	
	n = int(input())
	print(dp[n])

[forminator_quiz id="2074"]

This article tried to discuss the concept of Dynamic Programming. Hope this blog helps you understand and solve the problem. To practice more problems on Dynamic Programming you can check out MYCODE | Competitive Programming.