Last Updated on June 9, 2023 by Mayank Dham

LCS, which stands for "Longest Common Subsequence" is a fundamental problem in computer science and bioinformatics. It involves finding the longest subsequence that is common to two or more sequences.
A subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements.
The LCS problem has numerous applications, including text comparison, DNA sequence alignment, version control systems, and plagiarism detection. It is commonly used to determine the similarity or dissimilarity between sequences and to identify shared patterns or structures.
CONCEPTS USED:
Dynamic programming
DIFFICULTY LEVEL:
Medium.
PROBLEM STATEMENT(SIMPLIFIED):
PrepBuddy is too good with string observations but now the Dark Lord thought to defeat PrepBuddy.
So he gave him two strings and told him to find the length of the longest common subsequence.
For Example :
> aabbcc abcc
In this example "abcc" is the longest common subsequence.
>prep rep
"rep" is the longest common subsequence here.OBSERVATION:
The question demands you to find the longest subsequence .
What is a subsequence?A subsequence is a sequence that can be derived from another sequence by zero or more elements, without changing the order of the remaining elements. Suppose,X and Y are two sequences over a finite set of elements. We can say that Z is a common subsequence of X and Y, if Z is a subsequence of both X and Y.
SOLVING APPROACH:
Brute Force:
We need to first find the number of possible different subsequences of a string with length n, i.e., find the number of subsequences with lengths ranging from 1,2,..n-1.
Number of subsequences of length 1 are: nC1.Similarly,Number of subsequences of length 2 are: nC2 and so on and so forth.This gives –
nC0+nC1+nC2+nC3+…+nCn-1+nCn=2n.
Can you find the time complexity of this brute force?A string of length n has 2n-1 different possible subsequences since we do not consider the subsequence with length 0. This implies that the time complexity of the brute force approach will be O(n * 2n). Note that it takes O(n) time to check if a subsequence is common to both the strings. This time complexity can be improved using dynamic programming.
You are encouraged to try on your own ,before looking at the solution.
See original problem statement here
DYMANIC PROGRAMMING:
The problem of computing their longest common subsequence, or LCS, is a standard problem and can be done in O(nm) time using dynamic programming.
Let’s define the function f. Given i and i, define f(i,j) as the length of the longest common subsequence of the strings A1,i and B1,j. Notice that A=A1,n and B=B1,m , so the length of the LCS of A and B is just f(n,m), by definition of f. Thus, our goal is to compute f(n,m).
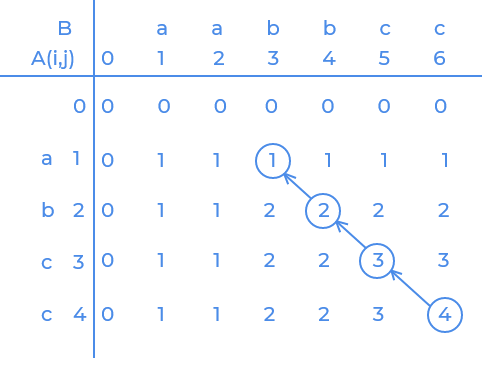
Look at the image carefully and observe how the table is filled.
So how do we compute f(i,j) ? Let’s consider the letters Ai and Bj. There are two cases:
If Ai==Bj, then the last letter of the LCS must be Ai, because if not, then we can just always add Ai at the end to get a longer LCS. The remaining letters of the LCS must then be a common subsequence of A1,i-1 and B1,j-1 — in fact a longest common subsequence. Therefore in this case, the length of the LCS of A1,i and B1,j must be f(i,j)=1+f(i-1,j-1).If Ai!=Bj, then Ai and Bj cannot both appear at the end of the longest common subsequence, which means either one can be ignored. If we ignore Ai , then the LCS of A1,i and B1,j becomes the LCS of A1,i-1 and B1,j, and if we ignore Bj, then the LCS becomes the LCS of A1,i and B1,j-1. The longer one of those must be the LCS of A1,i and B1,j, therefore in this case we get
f(i,j)=max(f(i-1,j),f(i,j-1)).
Pseudocode:
function f(i, j):
if i == 0 or j == 0:
return 0
else if A[i] == B[j]:
return 1 + f(i-1, j-1)
else:
return max(f(i-1, j), f(i, j-1))
// the answer is now f(n, m)SOLUTIONS:
#include <stdio.h>
#include<stdlib.h>
#include<string.h>
int max(int x,int y)
{
if(x>y)return x;
return y;
}
int main()
{
//write your code here
int t;scanf("%d",&t);
while(t--)
{
char s1[1005],s2[1002];
scanf("%s%s",s1,s2);
int dp[strlen(s1)+1][strlen(s2)+1];
int n=strlen(s1),m=strlen(s2);
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
if(i==0||j==0)
dp[i][j]=0;
else
{
if(s1[i-1]==s2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
printf("%d\n",dp[n][m]);
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
//write your code here
int t;cin>>t;
while(t--)
{
string s1,s2;
cin>>s1>>s2;
int dp[s1.length()+1][s2.length()+1];
int n=s1.length(),m=s2.length();
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
if(i==0||j==0)
dp[i][j]=0;
else
{
if(s1[i-1]==s2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[n][m]<<"\n";
}
return 0;
}
import java.util.*;
import java.io.*;
class LongestCommonSubsequence {
/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
public static int getLongestCommonSubsequence(String a, String b){
int m = a.length();
int n = b.length();
int[][] dp = new int[m+1][n+1];
for(int i=0; i<=m; i++){
for(int j=0; j<=n; j++){
if(i==0 || j==0){
dp[i][j]=0;
}else if(a.charAt(i-1)==b.charAt(j-1)){
dp[i][j] = 1 + dp[i-1][j-1];
}else{
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[m][n];
}
int max(int a, int b)
{
return (a > b) ? a : b;
}
/* Utility function to get max of 2 integers */
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int t= sc.nextInt();
while(t-- >0 ){
//LongestCommonSubsequence lcs = new LongestCommonSubsequence();
String s1= sc.nextLine();
String s2= sc.nextLine();
System.out.println(getLongestCommonSubsequence(s1,s2)); }
}
}
for _ in range(int(input())): s1, s2 = input().split() dp = [[0 for i in range(len(s2) + 1)] for j in range(len(s1) + 1)] n=len(s1) m=len(s2) for i in range(n + 1): for j in range(m + 1): if(i == 0 or j == 0): dp[i][j] = 0 else: if(s1[i - 1] == s2[j - 1]): dp[i][j] = dp[i - 1][j - 1] + 1 else: dp[i][j] = max(dp[i - 1][j],dp[i][j - 1]) print(dp[n][m])
Space complexity: O(N*M)
[forminator_quiz id="2115"]
This article tried to discuss Dynamic programming. Hope this blog helps you understand and solve the problem. To practice more problems on Dynamic programming you can check out MYCODE | Competitive Programming.
Conclusion
In conclusion, LCS (Longest Common Subsequence) is a significant problem in computer science and bioinformatics with various practical applications. It involves finding lcs using dynamic programming. By finding lcs using dynamic programming, we can determine the similarity or dissimilarity between sequences, identify shared patterns or structures, and make informed decisions based on the obtained insights.
The LCS problem has led to the development of efficient algorithms, such as dynamic programming-based approaches like the Needleman-Wunsch and Wagner-Fisher algorithms. These algorithms enable us to solve the LCS problem in an optimized manner, making it feasible to handle large-scale sequences.
Whether it is comparing texts, aligning DNA sequences, detecting plagiarism, or analyzing version control systems, LCS provides a foundation for understanding the relationships and similarities between sequences. By leveraging the LCS problem and its algorithms, we can unlock new possibilities in fields ranging from computational biology to software development and beyond.
Frequently Asked Questions
Q1. What is the difference between a subsequence and a substring?
A subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. In contrast, a substring is a contiguous sequence of characters or elements that appears consecutively in another sequence without any gaps.
Q2. Can the LCS problem be solved efficiently?
Yes, the LCS problem can be solved efficiently using dynamic programming-based algorithms. The Needleman-Wunsch and Wagner-Fisher algorithms are commonly used to find the longest common subsequence in an optimized manner. These algorithms have a time complexity of O(mn), where m and n are the lengths of the input sequences.
Q3. Are there any applications of LCS outside of computer science?
Yes, LCS has applications beyond computer science. It is commonly used in bioinformatics for DNA sequence alignment, where it helps identify similarities and patterns in genetic sequences. Additionally, LCS is utilized in plagiarism detection systems to compare texts and identify similarities between documents.
Q4. Can the LCS problem handle more than two input sequences?
Yes, the LCS problem can handle multiple input sequences. By extending the dynamic programming-based algorithms, such as the Needleman-Wunsch algorithm, it is possible to find the longest common subsequence among multiple sequences. This extended problem is known as the Longest Common Subsequence of k sequences (LCSSK).
Q5. Can LCS be used for approximate string matching?
No, LCS is not suitable for approximate string matching. It is specifically designed to find the longest common subsequence without allowing modifications like insertions, deletions, or substitutions. For approximate string matching, other algorithms such as the Levenshtein distance or the Smith-Waterman algorithm are commonly used.