Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Heap

Print first K non-repeating characters of a string

Deepak

Last Updated on March 28, 2022 by Ria Pathak

Concepts Used:

Heap

Difficulty Level:

Hard

Problem Statement :

Given a string str, find first K non-repeating characters in lexicographical order, if all the characters are repeating then print "Not Exist" without quotes.

See original problem statement here

Solution Approach :

Introduction :

We need to print first K characters in lexicographical order. We can use min-heap, each time we extract a character from our heap, we check the occurence of the character, if it is 1 then we will accept the character otherwise reject it.

Method 1 :

We can sort first k characters of the string using any sorting algorithm, now store the frequency of each character of the string. Now take the first k characters which are not repeated and print them.

Method 2 :

We need to geneate a min heap of characters of size k.
In a min-heap, the root always stores the smaller value as compared to its left & right subtree, this condition needs to be true for every node. We need to insert each item one by one such that it’s parent is always smaller than the item itself. If the parent is greater, then we need to swap the current item with its parent.

We will insert first k characters from str which are non repeating, in the heap. We can keep track of the frequency of each character in str using frequency array. Once we are done creating heap for first k non repeating characters, we will extract all characters one-by-one and print it,
if all the characters in str are repeating print "Not Exist" without quotes.

extract(): Removes the minimum element from Min-Heap. Time Complexity of this Operation is O(Logn) as this operation needs to maintain the heap property (by calling heapify()) after removing root.

heapify(): Maintains the heap property for each node. If any node does not follow heap property it swaps the node with the node which is smaller ,or greater (in case of max-heap), than the node.

Algorithms :

Insert():

  1. Insert the item at the last index, and increment the size by 1.
  2. Then, check if the inserted item is smaller than its parent,
  3. If yes, then swap the inserted item with its parent.
  4. If no, then do nothing.
  5. Now, go to step 2 and repeat untill we reach root (first element).

Extract() :

  1. Store the value of the first node of our heap ( temp = heap[0] ).
  2. Replace the root node with the farthest right node (last element).
  3. Decrease the size by 1. (heap[0] = heap[size-1])
  4. Perform heapify starting from the new root.
  5. Return the stored value.(temp)

Heapify():

  1. if the heap property holds true then you are done.
  2. else if
  3. the replacement node value <= its parent nodes value
    then swap them, and repeat step 3.
  4. else
  5. swap the replacement node with the smallest child node, and
    repeat step 3.

Example:


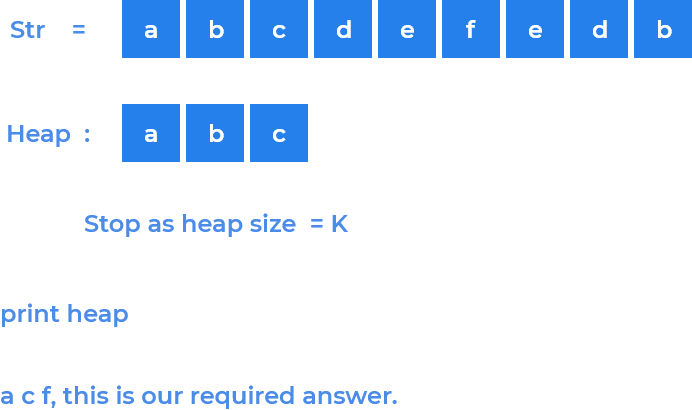
Solutions:

#include <stdio.h>
#include<stdlib.h>
#define INT_MIN -99999
void swap(int *a,int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int parent(int i)
{
return (i/2);
}
int left(int i)
{
return (i*2);
}
int right(int i)
{
return (i*2)+1;
}
void insert(int heap[],int *size,int val)
{

int i = (*size);
*size +=1;
heap[i] = val;
while(i!=1 && heap[parent(i)]>heap[i])
{
    swap(&heap[parent(i)],&heap[i]);
    i = parent(i);
}
int extract(int heap[],int *size)
{
    int root = heap[1];
    heap[1] = heap[(*size)-1];
    (*size)--;
    return root;
}
void heapify(int heap[],int i,int size)
{
int l = left(i);
int r = right(i);
int s = i;
if(l<size && heap[l]< heap[i])
s = l;
if(r<size && heap[r]< heap[s])
s = r;

if(s!=i)
{
    swap(&heap[i],&heap[s]);
    heapify(heap,s,size);
}
}
void removee(int heap[],int i,int *size)
{
heap[i] = INT_MIN;
while(i!=1 && heap[parent(i)]>heap[i])
{
    swap(&heap[parent(i)],&heap[i]);
    i = parent(i);
}
extract(heap,size);
heapify(heap,1,*size);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,k;
int size = 1;
scanf("%d %d", &n,&k);
int *heap =(int*) malloc(sizeof(int)*(n+1));
int a[n];
for(int i = 0;i<n;i++)
{
    scanf("%d", &a[i]);
    insert(heap,&size,a[i]);
}

removee(heap,k,&size);

for(int j=1;j<size;j++)
    printf("%d ", heap[j]);
    printf("\n");

}

return 0;
}

#include<bits/stdc++.h>
using namespace std;
int parent(int i)
{
     return (i-1)/2;
}
int left(int i)
{
     return (i*2)+1;
}
int right(int i)
{
     return (i*2)+2;
}
void swap(char *a,char *b)
{
     char temp = *a;
     *a = *b;
     *b = temp;
}
void insert(char heap[],int *size,char val)
{
     heap[*size] = val;
     int i = *size;
     (*size)++;
     while(i!=0 && heap[parent(i)]> heap[i])
     {
     swap(&heap[parent(i)],&heap[i]);
     i = parent(i);
     }
}
void heapify(char heap[],int i,int size)
{
     int l = left(i);
     int r = right(i);
     int s = i;
     if(l<size && heap[l]<heap[i])
     s = l;
     if(r<size && heap[r]<heap[s])
     s = r;
     if(s!=i)
     {
     swap(&heap[i],&heap[s]);
     heapify(heap,s,size);
     }
}
char extract(char heap[], int *size)
{
     char root = heap[0];
     heap[0]= heap[(*size)-1];
     (*size)--;
     heapify(heap,0,*size);
     return root;
}
int main()
{
     int t;
     cin>>t;
     while(t--)
     {
     int k;
     cin>>k;           
     char hash[27]={0};
     string str;
     cin>>str;
     int n = str.length();
     char *heap = (char*)malloc(sizeof(char)*(k+1));
     int size = 0;
     for(int i=0;i<n;i++)
     {
     hash[str[i]-'a']++;
     }

     int count = 1;
     for(int i=0;i<n;i++)
     {
     if(hash[str[i]-'a']==1 && count<=k )
     {
     insert(heap,&size,str[i]);
     count++;
     }
     }

     if(count==1)
     {
     cout<<"Not Exist"<<endl;
     continue;
     }
     int c = size;
     while(c--)
     {
     cout<<extract(heap,&size);
     // printf(" %d ", n);
     }
     cout<<endl;
     }
     return 0;
}

import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int t=sc.nextInt();
        while(t-->0) {
            int n = sc.nextInt();
            int k = sc.nextInt();
            MinHeap minHeap = new MinHeap(n);
            for (int i = 0; i < n; i++) {
                minHeap.insert(sc.nextInt());
            }
            minHeap.deleteKey(k);
            minHeap.printHeap(sc);
            System.out.println();
        }
        }
}
class MinHeap
{
    private int[]Heap;
    private int size;
    private int maxSize;
    private static final int FRONT = 1;
    MinHeap(int maxSize)
    {
        this.maxSize = maxSize;
        size=0;
        Heap = new int[this.maxSize+1];
        Heap[0] = Integer.MIN_VALUE;
    }
    private int parent(int pos) {
        return pos / 2;
    }
    private int leftChild(int pos)
    {
        return (2*pos);
    }
    private int rightChild(int pos)
    {
        return (2*pos)+1;
    }
    private boolean isLeaf(int pos)
    {
        if(pos>=(size/2) && pos<=size)
            return true;
        return false;
    }
    private void swap(int fpos, int spos)
    {
        int temp;
        temp = Heap[fpos];
        Heap[fpos]=Heap[spos];
        Heap[spos]=temp;
    }
    private void minHeapify(int pos)
    {
        int left = leftChild(pos);
        int right = rightChild(pos);
        int largest = pos;
        if(left<=size && Heap[left]<Heap[largest])
            largest=left;
        if(right<=size && Heap[right]<Heap[largest])
            largest = right;
        if(largest!=pos)
        {
            swap(pos, largest);
            minHeapify(largest);
        }
       }
    void insert(int element)
    {
        if(size>=maxSize)
            return;
        Heap[++size]=element;
        int i=size;
        while(Heap[i]<Heap[parent(i)])
        {
            swap(i,parent(i));
            i=parent(i);
        }
    }
    private void build_heap()
    {
        int j=(int)Math.floor(size/2.0);
        for(int i=j;i>=1;i--){
            minHeapify(i);
        }
    }
public void heapSort(Writer wr) throws IOException {
        build_heap();
        int length=size;
        for(int i=size;i>=2;i--)
        {
            swap(1,i);
            size--;
            minHeapify(1);
        }
        size=length;
    // printHeap(wr);
    }
    public int remove()
    {
        int popped = Heap[FRONT];
        Heap[FRONT] = Heap[size];
        size=size-1;
        minHeapify(FRONT);
        return popped;
    }
    public void deleteKey(int i)
    {
        decreaseKey(i, Integer.MIN_VALUE);
        remove();
    }
    private void decreaseKey(int i, int new_val) {
        Heap[i]=new_val;
        while(i !=0 && Heap[parent(i)]>Heap[i])
        {
            swap(i,parent(i));
            i=parent(i);
        }
    }
    void printHeap(Scanner sc) throws IOException {
        for(int i=1;i<=size;i++)
        {
            //wr.write(Heap[i]+" ");
            System.out.print(Heap[i]+" ");
        }
    }
}

[forminator_quiz id="1540"]

This article tried to discuss Heap. Hope this blog helps you understand and solve the problem. To practice more problems on heap you can check out MYCODE | Competitive Programming.

Leave a Reply

Your email address will not be published. Required fields are marked *

Close

Related Post