Rearrange the given linked list such that it consists of alternating minimum-maximum elements

Last Updated on December 13, 2022 by Prepbytes

This article taught you the most interesting and efficient problem of the linked list “Rearrange linked list in alternate last and first”. We will see the approach, algorithms, dry run, and code implementation. We hope this article will enhance your knowledge of the linked list. Let us understand the problem statement of Rearrange linked list in alternate last and first for a better understanding.

How to Rearrange linked list in alternate last and first

In this problem, we are given a LinkedList (root node) and we are asked to rearrange it such that after rearrangement, it will contain alternating minimum and maximum elements in the following format:

• The first element should be the minimum element.
• The second element should be the maximum element.
• The third element should be the next minimum and the fourth element should be the next maximum and so on.

Let’s see an example:
Input:

Output:

Let’s first understand the problem statement with the help of examples.

If the given linked list is: head →12 → 4 → 5 → 9 → 10 → 6.
We can form our output list having alternating minimum-maximum elements following the below steps.

• As 4 is the minimum element so, it will be the first element in the resultant list.

  • Resultant list after this step: head →4

• 12 is the maximum element so, it will be the second element in the resultant list.

  • Resultant list after this step: head →4 → 12

• 5 is the next minimum after 4 so, it is the third element.

  • Resultant list after this step: head →4 → 12 → 5

• 10 is the next maximum after 12 so, it is the fourth element.

  • Resultant list after this step: head →4 → 12 → 5 → 10

• 6 is the next minimum after 5 so, it is the fifth element.

  • Resultant list after this step: head →4 → 12 → 5 → 10 → 6

• 9 is the next maximum after 10 so, it is the sixth element.

  • Resultant list after this step: head →4 → 12 → 5 → 10 → 6 → 9

• Our final resultant linked list having alternating minimum-maximum elements will be: head →4 → 12 → 5 → 10 → 6 → 9

Now I think from the above examples, the problem statement is clear. So let’s see how we will approach it. Any Ideas?

• If not, it’s okay. We will see in the next section some helpful observations using which we will try to devise our algorithm.

Let’s move to the next section.

Helpful Observations of Rearrange linked list in alternate last and first

1. If we sort the given list we get:

   

2. If we reverse the sorted list after the middle element we get:

   

3. The first half of the linked list from observation 2, which contains linked list sorted in ascending order.

   

4. The second half of the linked list from observation 2, which contains linked list sorted in descending order.

   

Here, on careful observation we can see that our resultant list head →4 → 12 → 5 → 10 → 6 → 9 is nothing but just a combination of the alternate nodes from the two lists in observations 3 and 4. So, we will use this observation to create our algorithm.

Approach and Algorithm of Rearrange linked list in alternate last and first

• Sort the given list. Here, we will be using merge sort to sort the given list. You can sort the list using any sorting method you like.
• Get the middle element using the tortoise and hare approach. The tortoise and hare approach is an efficient way to find the middle element of a list.
• Reverse the list after the middle element and store it as a separate list.
• Create a new empty list pointed by the result pointer.
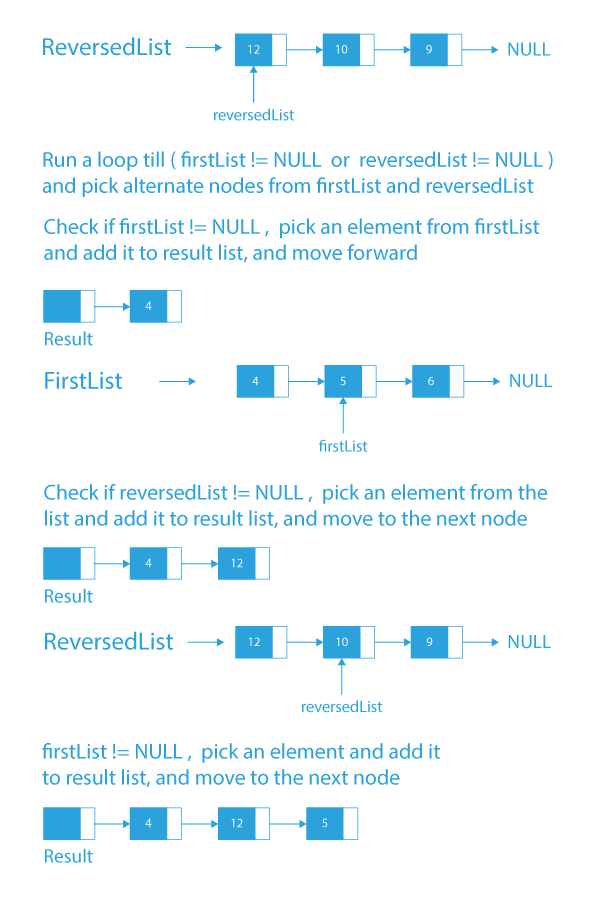
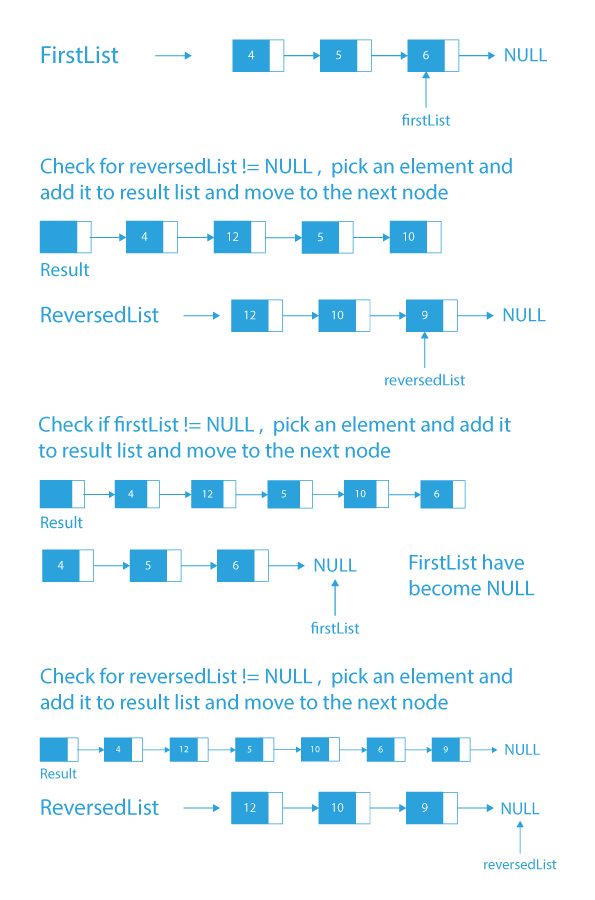
• Alternatively, add elements from the firstList and the reversedList starting with the firstList as we have to add in minimum and maximum order.
• After adding all the elements from the firstList and the reversedList into the list pointed by the result. The result will contain the required list having alternating minimum-maximum elements.

Dry Run of Rearrange linked list in alternate last and first

Code Implementation of Rearrange linked list in alternate last and first

public class Prepbytes {
    static class Node {
        int data;
        Node next;

        Node() {
        };

        Node(int num) {
            data = num;
            next = null;
        }
    };

    public static Node rearrangeListToHaveMinMaxElements(Node head) {
        if (head == null) {
            return head;
        }
 	   if (head.next == null) {
            return head;
        }

        head = getSortedList(head);

        Node mid = getMidNode(head);
        Node secondList = mid.next;
        mid.next = null;

        Node reversedList = getReversedList(secondList);
        Node firstList = head;

        Node result = new Node();
        Node node = result;

        while (firstList != null || reversedList != null) {

            if (firstList != null) {
                node.next = firstList;
                node = node.next;
                firstList = firstList.next;
            }

            if (reversedList != null) {
                node.next = reversedList;
                node = node.next;
                reversedList = reversedList.next;
            }
        }

        return result.next;
    }

    public static Node getSortedList(Node node) {
        if (node == null || node.next == null) {
            return node;
        }

        Node mid = getMidNode(node);
        Node next = mid.next;
        mid.next = null;

        Node lista = getSortedList(node);
        Node listb = getSortedList(next);

        return merge(lista, listb);
    }

    public static Node merge(Node lista, Node listb) {
        if (lista == null && listb == null) {
            return null;
        }

        Node temp = new Node();
        Node mergedList = temp;
        
        while (lista != null && listb != null) {
            
            if (lista.data < listb.data) {
                temp.next = lista;
                lista = lista.next;
            } else {
                temp.next = listb;
                listb = listb.next;
            }

            temp = temp.next;
        }
        if (lista != null) {
            temp.next = lista;
        } 
   else {
            temp.next = listb;
        }

        return mergedList.next;
    }

    public static Node getMidNode(Node node) {
        Node slow = node;
        Node fast = node;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    public static Node getReversedList(Node node) {
        if (node == null || node.next == null) {
            return node;
        }

        Node prev = null;
        Node next = null;

        while (node != null) {
            next = node.next;
            node.next = prev;
            prev = node;
            node = next;
        }

        return prev;
    }

    public static void main(String[] args) {
        Node head = new Node(12);
        head.next = new Node(4);
        head.next.next = new Node(5);
        head.next.next.next = new Node(9);
        head.next.next.next.next = new Node(10);
        head.next.next.next.next.next = new Node(6);

        head = rearrangeListToHaveMinMaxElements(head);
        while (head != null) {
            System.out.print(head.data + " ");
            head = head.next;
        }
    }
}

# A Linked List Node
class Node:
    def __init__(self, data=None, next=None):
        self.data = data
        self.next = next
 
 
# Function to print a given linked list
def printList(head):
 
    ptr = head
    while ptr:
        print(ptr.data, end=' ')
        ptr = ptr.next
 
 
 
# Rearrange the linked list so that it has alternating high, low values
def rearrange(head):
 
    # empty list
    if head is None:
        return None
 
    prev = head
    curr = head.next
 
    # start from the second node
    while curr:
 
        # if the previous node is greater than the current node, swap their values
        if prev.data > curr.data:
            temp = prev.data
            prev.data = curr.data
            curr.data = temp
 
        # if the next node is greater than the current node, swap their values
        if curr.next and curr.next.data > curr.data:
            temp = curr.next.data
            curr.next.data = curr.data
            curr.data = temp
 
        # update `prev` and `curr` node
        prev = curr.next
 
        if curr.next is None:
            break
 
        curr = curr.next.next
 
    return head
 
 
if __name__ == '__main__':
 
    # input keys
    keys = [12, 4, 5, 9, 10, 6]
 
    head = None
    for i in reversed(range(len(keys))):
        head = Node(keys[i], head)
 
    head = rearrange(head)
    printList(head)

Output
4 12 5 10 6 9

Time Complexity of Rearrange linked list in alternate last and first: O(n*logn), where n is the number of nodes.

• O(n*logn) time is used to sort the list.
• O(n) time is used to find the mid element.
• O(n) time is used to reverse the list.
• O(n) to create the resultant list from the first list and reversed list.
  Summing up we get O(nlogn + n + n + n) = O(nlogn).

Conclusion

So, in this blog, we have tried to explain the Rearrange linked list in alternate last and first such that it consists of alternating minimum-maximum elements in the most efficient way. We hope you were able to take away critical techniques likes reversing a linked list slow and fast pointer approach, a two-pointer approach, etc. Also, If you want to solve more problems on Linked List, which our expert mentors at PrepBytes curate, you can follow this link Linked List.

FAQs related to Rearrange linked list in alternate last and first

1. How do I return a linked list size?
There are many ways we can return a linked list’s size. The first way is to traverse the list and increment the size when each node is visited. This is an O(n) approach. But suppose we want to answer online queries, then manipulating the size while adding and deleting nodes will help answer each question to find the size of the list, which will be O(1).

2. How do you reverse a linked list in K groups?
Reversing a linked list in K groups can be done recursively and iteratively. For each group of k elements starting from the root node, the basic concept is to reverse the k group linked list and then move to the head of the next group of K elements if it exists in the linked list. Repeat the same process until it reaches termination.

3. How do you reorder a linked list?
Reordering a linked list can be done using many techniques such as slow-fast pointers, two-pointers, recursion, etc.

4. Why do we need a dummy node in the linked list?
A dummy node is needed to carry out the operations of the linked list. Since we need to manipulate pointers within the linked list, we might lose the actual linked list if we manipulate without using a dummy pointer.