Find pairs with given sum in Sorted Doubly Linked List

Last Updated on November 23, 2022 by Prepbytes

Previously we have seen many articles of doubly linked list, In this article, we will have another problem of doubly linked list in which we have to find pairs with given sum in doubly linked list. A doubly linked list is a type of linked list in which we have three parts of a node i.e. the data, the pointer of the previous node, and the pointer of the next node. Let us take a look at the problem statement for a better understanding.

How to find pairs with given sum in doubly linked list

In this problem, we are given a sorted Doubly Linked List of distinct integers and we are asked to find the pair of nodes whose sum is equal to the given sum.

In this problem, we need to find the pair of nodes from the Linked list whose sum is equal to the given sum, which means we need to find pairs of such nodes whose addition gives the required sum.

Let’s first understand the problem statement with the help of examples.
If the given linked list is:

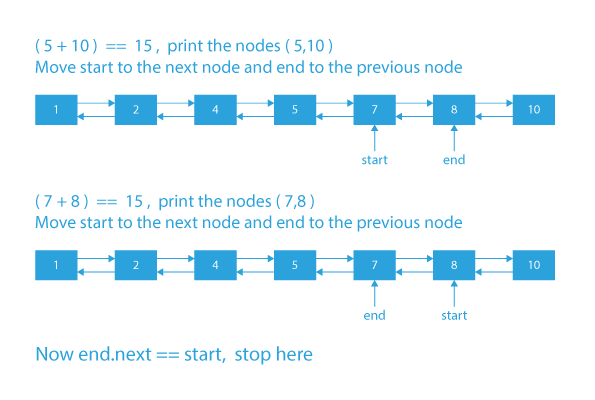
• Then, according to the problem statement, out of all the possible pairs from the linked list there are only 2 pairs that have a sum equal to 15 and those pairs are (5,10) and (7,8).
• So we will output the pairs (5,10) and (7,8).

If the given linked list is: head 1 2 5 6 8 9 10 and X(Given sum) = 7.

• In this case there are also only 2 pairs having a sum equal to 7 and those pairs are (1,6) and (2,5).
• So we will output the pairs (1,6) and (2,5).

Some more examples

Sample Input 1: head 1 3 5, X = 8.
Sample Output 1: (3,5)

Sample Input 2: head 2 4 6 8 10, X = 10.
Sample Output 2: (2,8), (4,6)

Now I think from the above examples, the problem statement is clear. So let’s see how we will approach it. Any Ideas?

• If not, it’s okay. We will see in the next section thoroughly how we can approach this problem.

Let’s move to the next section.

Approach 1 of how to find pairs with given sum in doubly linked list

The brute force approach for this problem can be to pick each node one by one and find another element whose sum is equal to the required sum by using two loops.

Time Complexity of how to find pairs with given sum in doubly linked list : O(n²)

Space Complexity of how to find pairs with given sum in doubly linked list : O(1)

This approach has a time complexity of O(n²), which means that for a linked list of bigger size greater than or equal to 10⁴, it will not be ideal to use this approach. So what should we do? Should we try to come up with an algorithm that can do our job in lesser time complexity?

• Yes, we should try to find some algorithm that can solve the problem efficiently.

So let’s see how we reduce the time complexity.

Approach 2 of how to find pairs with given sum in doubly linked list

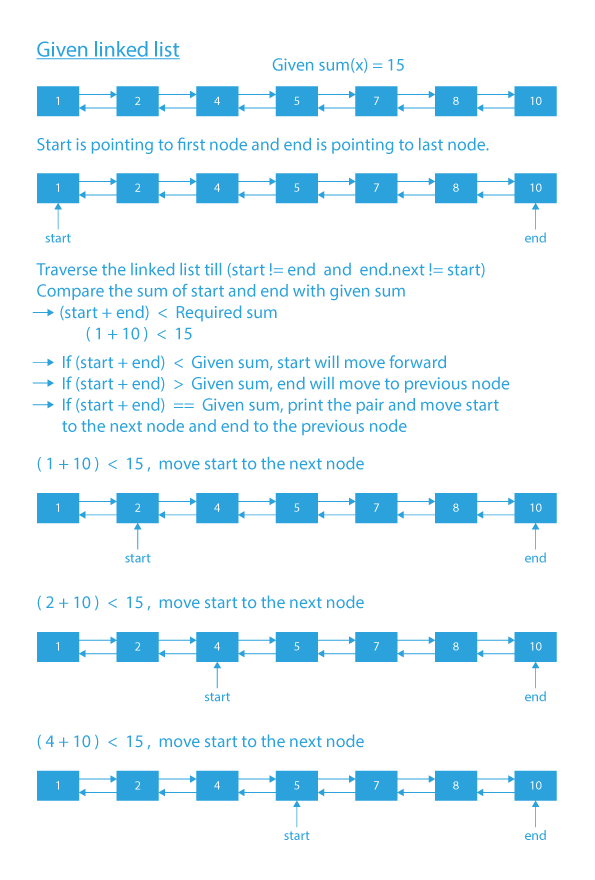
In order to find a pair with a given sum in a sorted Doubly Linked List, we can use the two-pointer algorithm by keeping one pointer(start) at the head and another(end) at the end of the list as we can traverse both ways. After keeping the pointers at the desired location, we will compare the sum of pairs with the given sum. There can be three conditions possible:

• The sum of pairs is less than the given sum. In this case, we will move the start pointer to its next node as we need a bigger number for the required sum.
• The sum of pairs is less than the given sum. In this case, we will move the end pointer to its previous node as we need a smaller number for the required sum.
• The sum of pairs is equal to the given sum. In this case, we will output this pair and move both start and end pointers to their next and previous nodes, respectively.

Let’s see the algorithm for the above approach.

Algorithm of how to find pairs with given sum in doubly linked list

• Create a start pointer and initialize it to the head node of the linked list.
• Create an end pointer and initialize it to the last node of the list.
• Calculate the sum of values in the nodes to which start and end are pointing (start.data + end.data) and compare this sum with the given sum:
  • If the sum of pairs is less than the given sum, move the start pointer to its next node.
  • If the sum of pairs is less than the given sum, move the end pointer to its previous node.
  • If the sum of pairs is equal to the given sum. In this case, we will output this pair and move both start and end pointers to their next and previous nodes respectively.
• Perform the above operations while (start!=end) or (start != end.next).

Dry Run of how to find pairs with given sum in doubly linked list

Code Implementation

#include
using namespace std;

/* Node structure of a doubly linked list */
struct Node
{
	int data;
	struct Node *next, *prev;
};

/* Using this function we will find pair having sum equal to X. */
void pair_sum(struct Node *head, int X)
{
	struct Node *start = head;
	struct Node *end = head;
	while (end->next != NULL)
		end = end->next;

	bool found = false;

	while (start != end && end->next != start)
	{
		if ((start->data + end->data) == X)
		{
			found = true;
			cout << "(" << start->data<< ", "
				<< end->data << ")" << endl;

			start = start->next;

			end = end->prev;
		}
		else
		{
			if ((start->data + end->data) < X)
				start = start->next;
			else
				end = end->prev;
		}
	}

	if (found == false)
		cout << "No pair with given sum exists";
}

/* Using this function we will insert new node in the linked list at beginning*/
void insertAtHead(struct Node **head, int data)
{
	struct Node *temp = new Node;
	temp->data = data;
	temp->next = temp->prev = NULL;
	if (!(*head))
		(*head) = temp;
	else
	{
		temp->next = *head;
		(*head)->prev = temp;
		(*head) = temp;
	}
}

int main()
{
	struct Node *head = NULL;
	insertAtHead(&head, 10);
	insertAtHead(&head, 8);
	insertAtHead(&head, 7);
	insertAtHead(&head, 5);
	insertAtHead(&head, 4);
	insertAtHead(&head, 2);
	insertAtHead(&head, 1);
	int X = 15;

	pair_sum(head, X);

	return 0;
}

Output
(5,10)
(7,8)

Time Complexity of how to find pairs with given sum in doubly linked list : O(n), where n is the number of nodes. We are traversing the list and traversing takes O(n) time.

Conclusion

So, in this blog, we have explained the most effective and efficient approach, an algorithm, and the implementation with a dry run of how you can find pairs with given sum in doubly linked list. Also If you want to solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.

FAQs related to how to find pairs with given sum in doubly linked list

1. How do you find the sum of two linked lists using stack?
We can find the sum of two linked lists using stack:

• Calculate the size of the given linked lists.
• If the size of the lists is the same then find using the recursion.
• Hold all the nodes and call stack till the rightmost node.
• Calculate the sum of the rightmost nodes and forward carry to the left side.

2. What is the sum of adding 1 to 100?
The sum of the number by adding 1 to 100 is 5050.

3. How do you traverse a doubly linked list?
Traversing is the most common operation in the case of each data structure. For this purpose, copy the head pointer in any of the temporary pointer ptr. then, traverse through the list by using a while loop.