Last Updated on November 22, 2022 by Prepbytes

We have seen various approaches and various types of deletion in linked lists such as Deleting a linked list, deleting the first node of linked list, deleting the last node of linked list, deleting the middle node of linked list and deleting the smaller and larger nodes of linked list. Now in the below article we will see how to delete alternate nodes of a linked list.
How to Delete Alternate Nodes of a Linked List.
Given a singly linked list. Remove its alternate nodes.
Example
Sample Input: 3->5->2->6->8
Sample Output: 3->2->8
Here 5 and 6 were the nodes at alternate positions. So, we have removed them.
Sample Input: 3->5->2->6->8->7
Sample Output: 3->2->8
Here 5, 6, and 7 were nodes at alternate positions. So, we have removed them.In this problem, we have to delete alternate nodes of the given linked list. Deleting alternate nodes means deleting nodes at alternate positions in the linked list.
Let’s understand this:
Consider a linked list 3->5->2->6->8->7 and lets mark the positions of the node (Using 1 based indexing).

If we start from position 1, the alternate nodes are at positions 2, 4, and 6.
Can you observe something about the alternate positions?
Now, hopefully i think it is clear what we have to do in this problem.
Approach (Iterative) of how to delete alternate nodes of a linked list
I hope you have understood the problem and have got a basic idea of what we are going to do.
We can observe from the above example that the alternate positions are the positions that are even. So, deleting alternate nodes becomes deleting nodes at even positions in the linked list. To do so, the idea is simple, while iterating through the linked list we need to keep a track of the node’s position and a pointer to the previous node. After reaching an even position, we just need to remove that node from the linked list and move ahead.
Since it is clear what we need to do, take some time and think about how we are going to do it. Below is the algorithm explaining the steps we need to take to implement our idea.
Algorithm of how to delete alternate nodes of a linked list
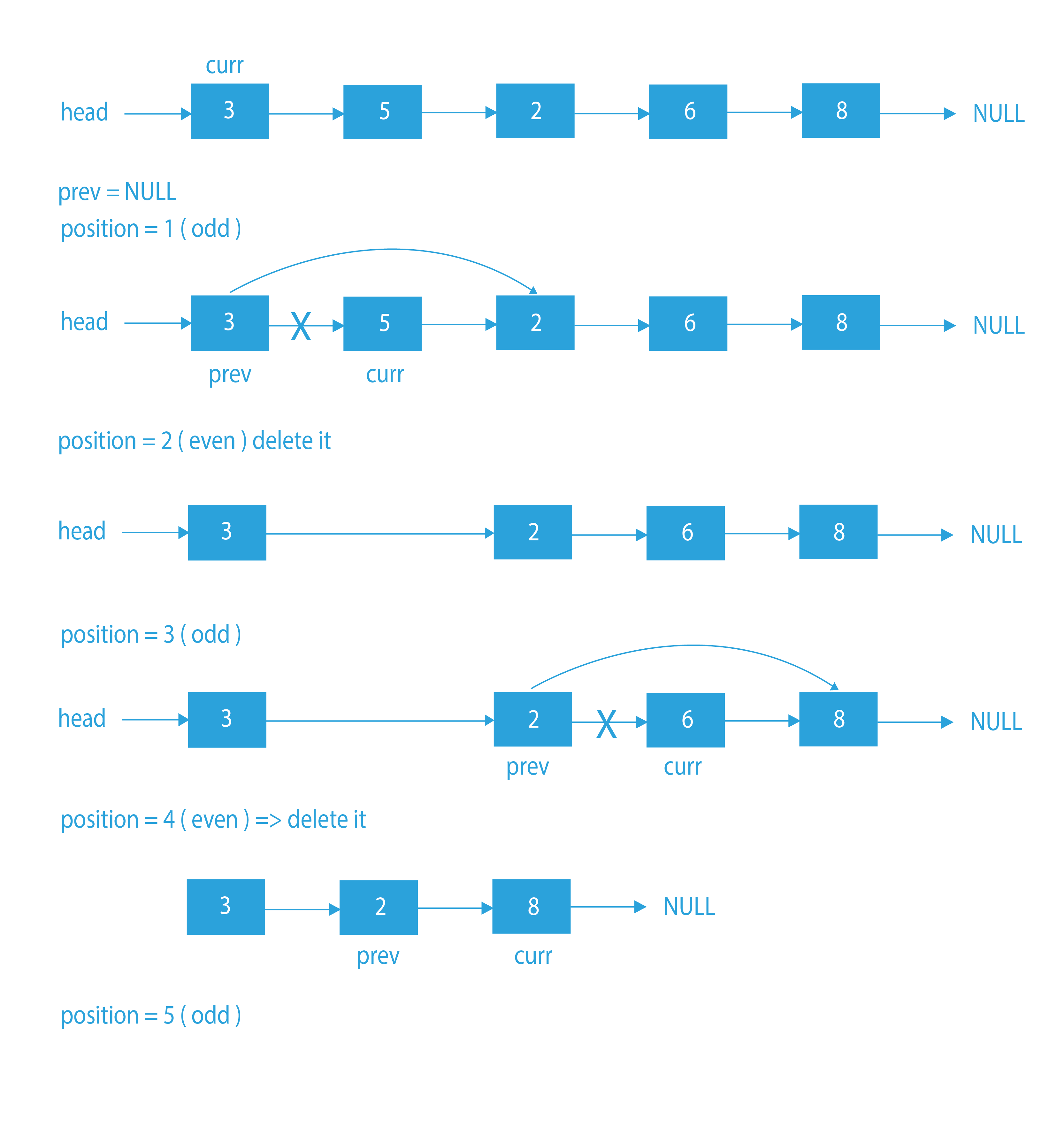
- Declare three variables: ‘curr’, ‘position’ and ‘prev’.
- Initialize position as 1 and prev as ‘NULL’ and ‘curr’ to head.
- Iterate through the linked list using curr and update positions and prev.
- If we reach an even position, delete the node at that position from the linked list by connecting the previous node to the next node of curr and deleting the current node, and move ahead.
Dry Run of how to delete alternate nodes of a linked list
Code Implementation of how to delete alternate nodes of a linked list
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node *next;
};
void deleteAlt(struct Node *head)
{
if (head == NULL)
return;
struct Node *prev = head;
struct Node *node = head->next;
while (prev != NULL && node != NULL)
{
prev->next = node->next;
free(node);
prev = prev->next;
if (prev != NULL)
node = prev->next;
}
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(struct Node *node)
{
while (node != NULL)
{
printf("%d ", node->data);
node = node->next;
}
}
int main()
{
struct Node* head = NULL;
push(&head, 50);
push(&head, 40);
push(&head, 30);
push(&head, 20);
push(&head, 10);
printf("\nList before delete \n");
printList(head);
deleteAlt(head);
printf("\nList after delete \n");
printList(head);
return 0;
}
#include<bits stdc++.h="">
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
void delete_alt_nodes(Node* head){
int position = 1;
Node *prev = NULL;
Node *curr = head;
while(curr != NULL){
if(position%2==0){
// delete curr
prev->next = curr->next;
Node *temp = curr;
curr = curr->next;
delete temp;
}
else {
prev = curr;
curr = curr->next;
}
position ++;
}
}
int main(){
Node* head = NULL;
push_front(&head, 8);
push_front(&head, 6);
push_front(&head, 2);
push_front(&head, 5);
push_front(&head, 3);
cout<<”Original list:\n”;
printList(head);
// 3 5 2 6 8
delete_alt_nodes(head);
cout<<”After deleting alternate nodes:\n”;
printList(head);
// 3 2 8
}
// Java program to delete alternate nodes of a linked list
class AlternateNodes
{
static Node head; // head of list
/* Linked list Node*/
class Node
{
int data;
Node next;
Node(int d) {data = d; next = null; }
}
void deleteAlt()
{
if (head == null)
return;
Node prev = head;
Node now = head.next;
while (prev != null && now != null)
{
/* Change next link of previous node */
prev.next = now.next;
/* Free node */
now = null;
/*Update prev and now */
prev = prev.next;
if (prev != null)
now = prev.next;
}
}
/* Utility functions */
/* Inserts a new Node at front of the list. */
public void push(int new_data)
{
/* 1 & 2: Allocate the Node &
Put in the data*/
Node new_node = new Node(new_data);
/* 3. Make next of new Node as head */
new_node.next = head;
/* 4. Move the head to point to new Node */
head = new_node;
}
/* Function to print linked list */
void printList()
{
Node temp = head;
while(temp != null)
{
System.out.print(temp.data+" ");
temp = temp.next;
}
System.out.println();
}
/* Driver program to test above functions */
public static void main(String args[])
{
AlternateNodes llist = new AlternateNodes();
/* Constructed Linked List is 1->2->3->4->5->null */
llist.push(8);
llist.push(6);
llist.push(2);
llist.push(5);
llist.push(3);
System.out.println("Linked List before calling deleteAlt() ");
llist.printList();
llist.deleteAlt();
System.out.println("Linked List after calling deleteAlt() ");
llist.printList();
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def deleteAlt(head):
if (head == None):
return
prev = head
now = head.next
while (prev != None and now != None):
prev.next = now.next
now = None
prev = prev.next
if (prev != None):
now = prev.next
def push(head_ref, new_data):
new_node = Node(new_data)
new_node.data = new_data
new_node.next = head_ref
head_ref = new_node
return head_ref
def printList(node):
while (node != None):
print(node.data, end = " ")
node = node.next
if __name__=='__main__':
head = None
head = push(head, 8)
head = push(head, 6)
head = push(head, 2)
head = push(head, 5)
head = push(head, 3)
print("List before calling deleteAlt() ")
printList(head)
deleteAlt(head)
print("\nList after calling deleteAlt() ")
printList(head)
Output
Original list: 3 5 2 6 8
After deleting alternate nodes: 3 2 8Time complexity to delete alternate nodes of a linked list : O(n), where n is the number of nodes in the linked list.
Space complexity to delete alternate nodes of a linked list: O(1), since we don’t use any extra space.
I hope you have understood the iterative approach. Now, let’s see another way to approach the problem.
Approach (Recursive) to delete alternate nodes of a linked list
We already know what deleting alternate nodes of a linked list means.
If we start from the first node we delete the second node and fourth node and so on. Given a linked list with at least 2 nodes and a given pointer to the first node we can easily delete the second node by making the ‘next’ of the first node as next of the first. Deleting the fourth node would be the same if we consider the linked list starting from the third node. Then the node to delete would be the 2nd node in that linked list.
Here we broke the given problem into a smaller problem. We delete the second node from the given linked list and call the same function for the linked list starting from the third node.
Now, what will be the base case?
If the linked list is empty or has only one node, we don’t have a second node to delete. So, we simply return the passed linked list.
Now that you have understood the approach, try to implement this idea yourself.
Algorithm to delete alternate nodes of a linked list
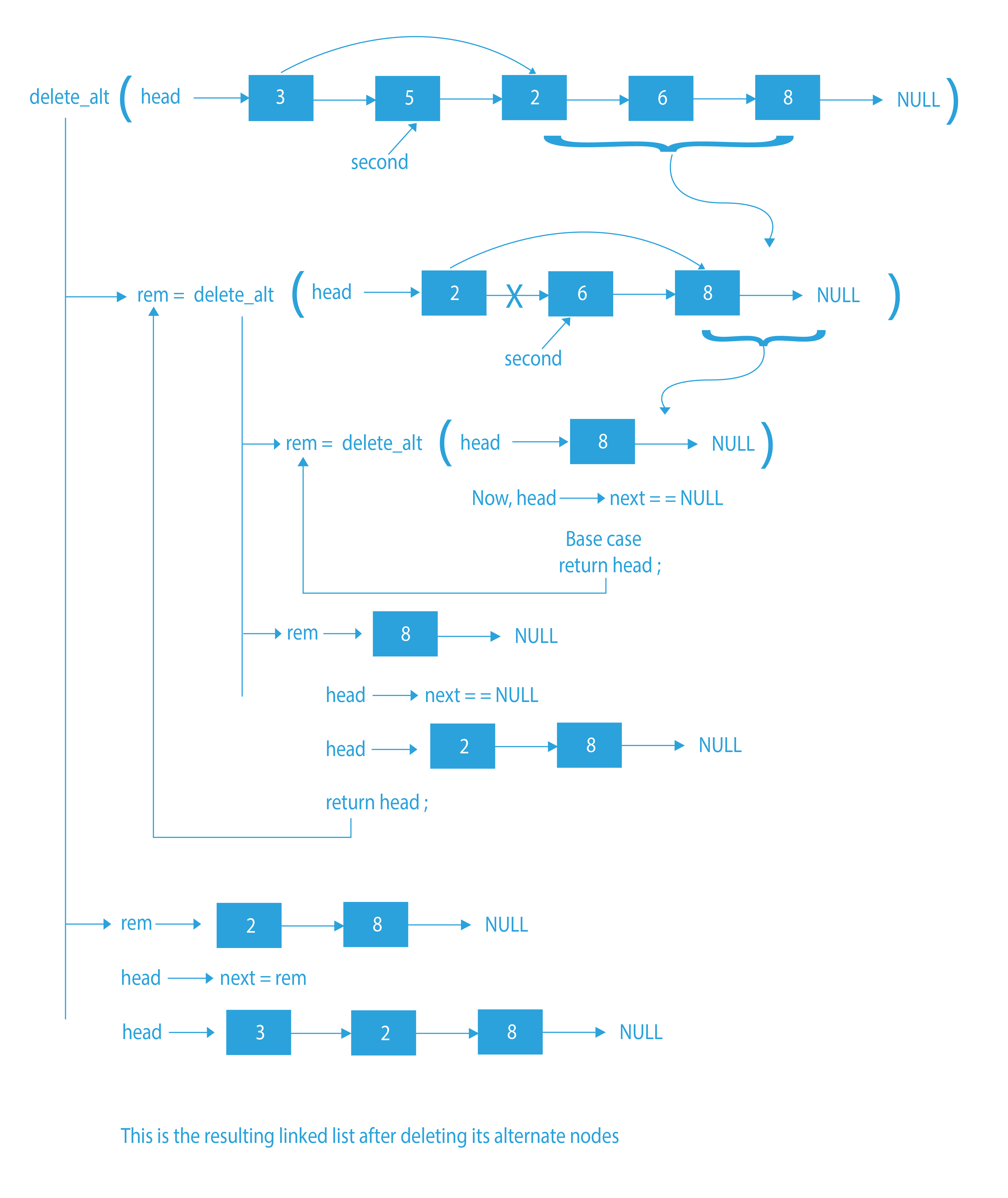
- If the linked list is empty or has only one node, return the linked list. (Base case)
- Store the pointer to the second node in a variable ‘second’ as: second = head->next.
- Recursively call the same function for the linked list after the 2nd node and store the linked list returned as ‘rem’.
- Attach this linked list pointed by ‘rem’ to the first node as: head->next = rem
- Now the second node is disconnected from the linked list, so delete it using the delete command.
- Return the resulting linked list.
Dry Run to delete alternate nodes of a linked list
Code Implementation to delete alternate nodes of a linked list
#include<stdio.h>
#include<stdlib.h>
struct Node {
int val;
struct Node* next;
};
void push_front(struct Node* head, int new_val){
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
new_node->next = head;
head = new_node;
}
void printList(struct Node* head){
struct Node* i = head;
while(i){
printf("%d ",&i->val);
i = i->next;
}
printf("\n");
}
// recursive function to delete alternate nodes of a linked list
struct Node* delete_alt(struct Node* head){
// base case
if(head==NULL || head->next==NULL) return head;
struct Node* second = head->next;
struct Node* rem = delete_alt(second->next);
head->next = rem;
free(second);
return head;
}
int main(){
struct Node* head = NULL;
push_front(&head, 8);
push_front(&head, 6);
push_front(&head, 2);
push_front(&head, 5);
push_front(&head, 3);
printList(head);
// 3 5 2 6 8
delete_alt(head);
printList(head);
// 3 2 8
}
#include<bits stdc++.h="">
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
// recursive function to delete alternate nodes of a linked list
Node* delete_alt(Node* head){
// base case
if(head==NULL || head->next==NULL) return head;
Node* second = head->next;
Node* rem = delete_alt(second->next);
head->next = rem;
delete second;
return head;
}
int main(){
Node* head = NULL;
push_front(&head, 8);
push_front(&head, 6);
push_front(&head, 2);
push_front(&head, 5);
push_front(&head, 3);
printList(head);
// 3 5 2 6 8
delete_alt(head);
printList(head);
// 3 2 8
}
// Java program to delete alternate nodes of a linked list
class AlternateNodes
{
static Node head; // head of list
/* Linked list Node*/
class Node
{
int data;
Node next;
Node(int d) {data = d; next = null; }
}
void deleteAlt()
{
if (head == null)
return;
Node prev = head;
Node now = head.next;
while (prev != null && now != null)
{
/* Change next link of previous node */
prev.next = now.next;
/* Free node */
now = null;
/*Update prev and now */
prev = prev.next;
if (prev != null)
now = prev.next;
}
}
/* Utility functions */
/* Inserts a new Node at front of the list. */
public void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
/* Function to print linked list */
void printList()
{
Node temp = head;
while(temp != null)
{
System.out.print(temp.data+" ");
temp = temp.next;
}
System.out.println();
}
/* Driver program to test above functions */
public static void main(String args[])
{
AlternateNodes llist = new AlternateNodes();
llist.push(8);
llist.push(6);
llist.push(2);
llist.push(5);
llist.push(3);
System.out.println("Linked List before calling deleteAlt() ");
llist.printList();
llist.deleteAlt();
System.out.println("Linked List after calling deleteAlt() ");
llist.printList();
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def deleteAlt(head):
if (head == None or head.next == None):
return head
second = head.next
rem = deleteAlt(second.next)
head.next = rem
del second
return head
def push(head_ref, new_data):
new_node = Node(new_data)
new_node.data = new_data
new_node.next = head_ref
head_ref = new_node
return head_ref
def printList(node):
while (node != None):
print(node.data, end = " ")
node = node.next
if __name__=='__main__':
head = None
head = push(head, 8)
head = push(head, 6)
head = push(head, 2)
head = push(head, 5)
head = push(head, 3)
print("List before calling deleteAlt() ")
printList(head)
deleteAlt(head)
print("\nList after calling deleteAlt() ")
printList(head)
Output
Original list: 3 5 2 6 8
After deleting alternate nodes: 3 2 8Space Complexity: O(n), due to function call stack, where n is the number of nodes in the linked list.
Conclusion
In the above article, we have seen how to initialize the singly linked list with dummy data and iterating through the list by maintaining the previous node and then deleting the alternate nodes. I would highly recommend you to practice more such problems from Linked List.
FAQs
1. Enlist the types of linked list?
- Singly linked list
- Doubly linked linked list
- Circular linked list
- Circular doubly linked list
2. Why is linked list preferred over other data structures?
Linked lists are preferred because of their efficient insertion and deletion , the other thing is the dynamic nature of linked lists.
3. Why is insertion faster in the linked list ?
As we already know that the linked list is dynamic in nature and there is just a rearrangement of pointers, no shifting and all.


