Flatten a multi-level linked list (Depth wise)

Last Updated on November 28, 2023 by Ankit Kochar

Flattening a multi-level linked list depth-wise involves transforming a nested structure into a flat, one-dimensional linked list. In this context, each node in the list may have a horizontal link to the next node at the same level and a vertical link to a sublist representing a lower level.

How to flattening a linked list?

The linked list that we have studied typically has only one pointer, i.e., a next pointer, which points to the next node in the linked list.

But, here in this problem, we have a linked list with 2 pointers named next and down.

• The next pointer points normally to the next node.
• But the down pointer points to a node that we assume is present in a node’s downward direction.

Our task is to flatten a linked list containing next and down pointers, and also we must make sure that we always process the down pointer before next at every node.

According to the problem statement, we have a linked list with 2 pointers named next and down, and we need to convert it to the normal linked list that we have studied earlier, i.e., we need to move nodes that are being pointed by the down pointer to next making all down pointers NULL, but also we need to keep in mind that we process down pointer before processing next pointer.

An alternate way to understand flattening a linked list, even more, is to imagine it as a binary tree (as shown in the image below).

• And now, all we need to do is to visit each node such that when we are at a current node then we need to first explore the nodes pointed by down pointer and when the list with current node’s down pointer is flattened completely, then we have to move towards node pointed by next pointer and perform the same task there also.

If say our given linked list is:

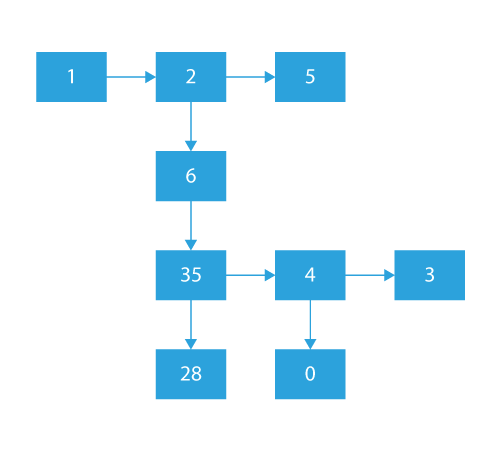
• In this case, our flattened list will be :

Now, we just need to perform a preorder traversal of the given linked list recursively, where down nodes will be flattened before the next nodes.

Approach for flattening a linked list

I hope that you got a basic idea of what we need to do to solve the flattening a linked list.

• The approach will be recursive; we have to consider the given list as a binary tree and traverse it in a preorder fashion.
• We have to first flatten the down nodes recursively and then the next nodes.
• Since we need to flatten the list:
  • So, we need to visit nodes present in the downward direction first.
  • We will keep a global pointer previous that would store the address of the current node to keep track of the last visited node.
  • And then, in each recursive call, we would be storing the next pointer and then call the recursive function for the down pointer first, and then will do the same for the next pointer afterwards.
• After performing the above steps, our list will get flattened.

Algorithm to flatten a multilevel linked list

• Base case: If the node is NULL, we do not need to do anything and we just return from recursion.

• Otherwise, store the address of the current node in a global variable previous to keep track of the last visited node.

• Store the current node’s next node in a variable next_node because at first, we will be processing down nodes, and not storing current node’s next will lead to loss of the next node and all its connected nodes.

• Then, we need to check whether the down node of the current node exists or not.

  • If it exists, we recursively call our function for the down node and flatten down nodes first and connect with current-> next.
  • current->next = flatten_linked_list(current->down).

• Then we check if the next node next_node (saved in step 3) exists or not.

  • If it exists, we again call the recursive function to flatten the linked list and connect it with previous-> next.
  • previous->next = flatten_linked_list(next_node)

• Finally, we return current.

Dry Run to flatten a multilevel linked list

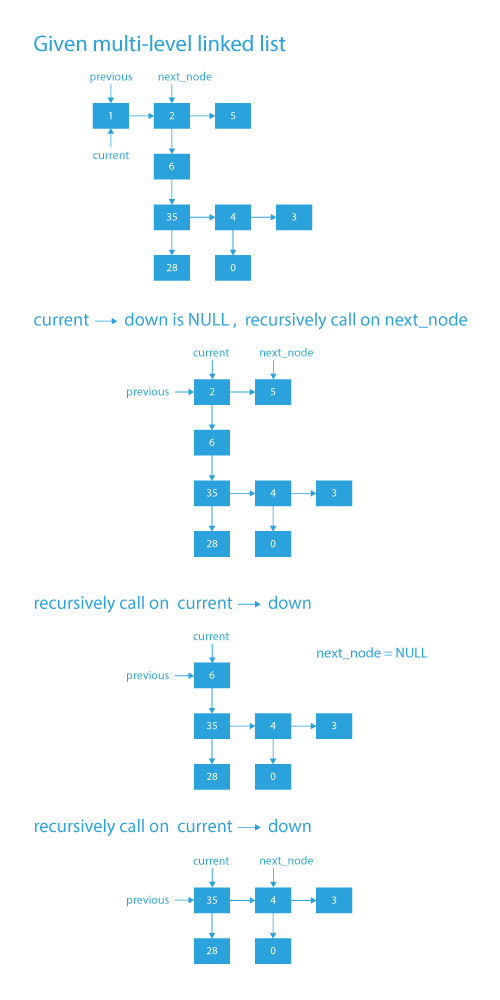
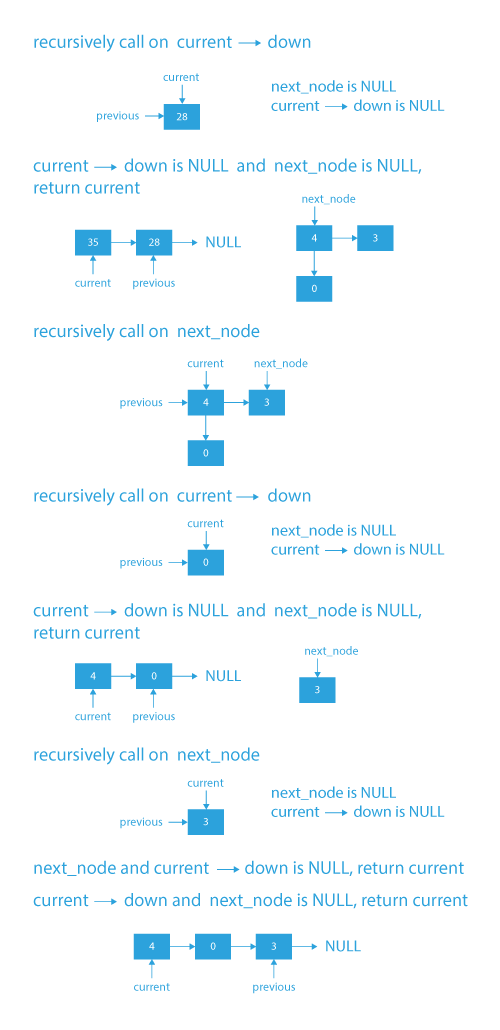
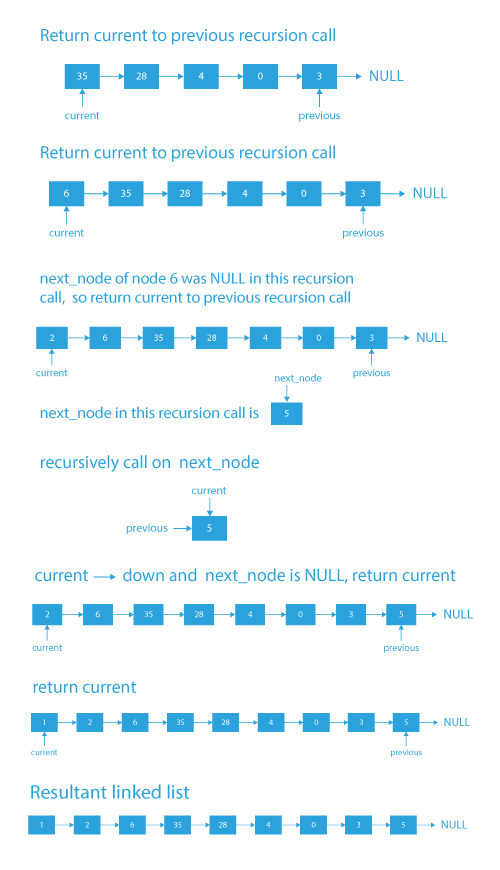
## Code Implementation of flattening a linked list

#include <stdio.h>
#include <stdlib.h>
struct Node
{
    int data;
    struct Node *next;
    struct Node *down;
};
 
// Flattens a multi-level linked list depth wise

struct Node* flattenList(struct Node* node)
{
    // Base case
    if (node == NULL)
        return NULL;
 
    // To keep track of last visited node
    // (NOTE: This is static)
    static struct Node* last;
    last = node;
 
    // Store next pointer
    struct Node *next = node->next;
 
    // If down list exists, process it first
    // Add down list as next of current node
    if (node->down)
       node->next = flattenList(node->down);
 
    // If next exists, add it after the next
    // of last added node
    if (next)
       last->next = flattenList(next);
 
    return node;
}
 
// Utility method to print a linked list
void printFlattenNodes(struct Node* head)
{
    while (head)
    {
    printf("%d ", head->data);
    head = head->next;
    }
    
}
 
// Utility function to create a new node
struct Node* newNode(int new_data)
{
    struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = new_node->down = NULL;
    return new_node;
}
 
// Driver code
int main()
{
    // Creating above example list
    struct Node* head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->down = newNode(7);
    head->next->down->down = newNode(9);
    head->next->down->down->down = newNode(14);
    head->next->down->down->down->down
                                     = newNode(15);
    head->next->down->down->down->down->next
                                     = newNode(23);
    head->next->down->down->down->down->next->down
                                      = newNode(24);
    head->next->down->next = newNode(8);
    head->next->down->next->down = newNode(16);
    head->next->down->next->down->down = newNode(17);
    head->next->down->next->down->down->next
                                      = newNode(18);
    head->next->down->next->down->down->next->next
                                      = newNode(19);
    head->next->down->next->down->down->next->next->next
                                      = newNode(20);
    head->next->down->next->down->down->next->next->next->down
                                      = newNode(21);
    head->next->down->next->next = newNode(10);
    head->next->down->next->next->down = newNode(11);
 
    head->next->down->next->next->next = newNode(12);
 
    // Flatten list and print modified list
    head = flattenList(head);
    printFlattenNodes(head);
 
    return 0;
}

#include <bits/stdc++.h>
using namespace std;

/* Structure of a linked list node */
struct Node
{
    int data;
    struct Node *next;
    struct Node *down;
};

/* Using this function we will be creating a new list node */
Node* createNode(int new_data)
{
    Node* new_node = new Node;
    new_node->data = new_data;
    new_node->next = new_node->down = NULL;
    return new_node;
}

/* The global node as discussed in step 2 */
Node *previous = NULL;

/* Using this function we will be flattening the multilevel linked list */
Node* flatten_linked_list(Node* current)
{
	// Base case
	if (current == NULL)
		return NULL;

	previous = current;// storing current node address as
	//discussed in step 2

	Node *next_node = current->next;// storing current
	// node’s next as discussed in step 3 

	// if down pointer of current node is not null then, we
	// process it first
	if (current->down != NULL)
	current->next = flatten_linked_list(current->down);
	// If the next node that we discussed in step 3 is not null
	// then we process it
	if (next_node != NULL)
	previous->next = flatten_linked_list(next_node);

	return current;
}

/* Using this function we will be printing the content of the linked list */
void print_linked_list(Node* head)
{
	while (head != NULL)
	{
		cout<<(head->data)<<" ";
		head = head->next;
	}
	cout<<endl;
}

/* Main driver function */
int main()
{
	Node* head = createNode(1);
	head->next = createNode(2);
	head->next->next = createNode(5);
	head->next->down = createNode(6);
	head->next->down->down = createNode(35);
	head->next->down->down->down = createNode(28);
	head->next->down->down->next = createNode(4);
	head->next->down->down->next->down = createNode(0);
	head->next->down->down->next->next = createNode(3);
	
	head = flatten_linked_list(head);
	cout<<"The linked list after flattening: ";
	print_linked_list(head);
	return 0;
}

class Node
{
    int data;
    Node next,down;
    Node(int data)
    {
        this.data=data;
        next=null;
        down=null;
    }
}
class Flatten 
{

    static Node last;

    // Flattens a multi-level linked list depth wise
    public static Node flattenList(Node node)
    {
        if(node==null)
            return null;

        // To keep track of last visited node
        // (NOTE: This is static)
        last = node;

        // Store next pointer
        Node next = node.next;

        // If down list exists, process it first
        // Add down list as next of current node
        if(node.down!=null)
            node.next = flattenList(node.down);

        // If next exists, add it after the next
        // of last added node
        if(next!=null)
            last.next = flattenList(next);

        return node;
    }
    public static void printFlattenNodes(Node head)
    {
        Node curr=head;
        while(curr!=null)
        {
            System.out.print(curr.data+" ");
            curr = curr.next;
        }
        
    }
    public static Node push(int newData)
    {
        Node newNode = new Node(newData);
        newNode.next =null;
        newNode.down = null;
        return newNode;
    }
    
    public static void main(String args[]) {
        Node head=new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(5);
        head.next.down = new Node(6);
        head.next.down.down = new Node(35);
        head.next.down.down.down = new Node(28);
        head.next.down.down.next= new Node(4);
        head.next.down.down.next.down= new Node(0);
        head.next.down.down.next.next = new Node(3);
        
        System.out.println("The linked list after flattening");
        head = flattenList(head);
        printFlattenNodes(head);
    }
}

Output
The linked list after flattening: 1 2 6 35 28 4 0 3 5

Time Complexity: O(n), where n is the number of nodes in the list.

**Conclusion**
Flattening a multi-level linked list depth-wise involves reorganizing a complex linked list structure, where nodes have both horizontal and vertical connections, into a single-level linked list that maintains the original order of elements

## FAQs related to Flatten a multi-level linked list (Depth wise)
Here are some FAQs related to Flatten a multi-level linked list (Depth wise):

**1. Why would I need to flatten a multi-level linked list?**
Flattening is beneficial when you want to simplify the structure for operations like searching, sorting, or printing elements. It transforms a hierarchical organization into a linear one.

**2. What is the significance of horizontal and vertical traversal in flattening?**
Horizontal traversal is used to connect nodes at the same level, while vertical traversal is necessary to explore and connect lower-level sublists. Both are essential for the flattening process.

**3. How does flattening impact the time complexity of operations?**
Flattening can improve the efficiency of certain operations by converting the structure to a linear form, making it easier to perform operations with a lower time complexity.

**4. Are there any challenges in implementing the flattening algorithm?**
Yes, implementing the algorithm requires careful management of pointers and connections to ensure the correct flattening of the linked list. Proper handling of edge cases, such as empty sublists, is crucial.

**5. Can flattening be done in-place, or does it require extra space?**
Flattening can often be done in-place, without requiring additional space, by appropriately adjusting pointers and connections during the traversal.