Last Updated on December 14, 2022 by Prepbytes

Several approaches exist in the programming world to solve this problem, some efficient and some not so efficient. Let us build the intuition to solve this problem brick by brick, by first discussing some simple methods, which are not so efficient. In this blog, we will see the problem merge k sorted lists using heap.
How to Merge K Sorted Lists using Heap
In this problem, we will be given K sorted linked lists. We need to merge all the lists such that the newly created list is also in sorted order.
The problem statement is quite straightforward, we will be given K sorted linked lists, and then we need to form a linked list using the nodes of all the given linked lists such that the newly formed list is sorted in order.
Let’s try to understand the problem with the help of examples:
If the sorted lists given to us are:
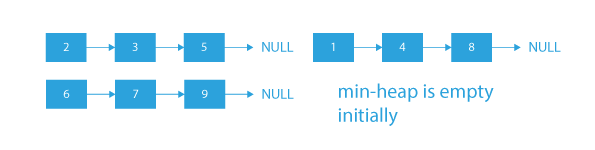
- According to the problem statement, we need to merge all these given linked lists into a single linked list in such a way that after merging, the final linked list is sorted in nature.
- The list that we need to return must contain all the nodes of all three given lists in sorted order.
- So, after merging the newly formed sorted list will be:

Let’s take another example:
If the sorted lists given to us be 2→8→9→10→NULL, 11→13→17→NULL.
- In this case, after merging, the final resultant sorted linked list will be 2→8→9→10→11→13→17→NULL.
At this point, we have understood the problem statement. Now we will try to formulate an approach for this problem.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Let’s move to the approach section.
Approach of how to merge k sorted lists using heap
In this approach, we will be using min heap.
- First, we need to create a min-heap.
- Since the smallest elements are present at the beginning of each list as each of them is sorted, so, we need to insert each list’s first element in our heap.
- Now, while our heap is not empty, we need to take out its top element and attach it at the end of our result list.
- The node which we attached to the end of the result list will be from one of the K given linked list, so if the next node of the node which we attached at the end of the result list exists, we need to push it into the min heap.
- Finally, when our min heap is empty, at that time the result list will contain all the nodes of the K given linked list in sorted order.
Algorithm of how to merge k sorted lists using heap
- Write a comparator function for the priority queue to store minimum elements at the top.
- Push starting node of all the lists in the min-heap.
- Now, create a node head with zero value that will act as a dummy node for our newly created list.
- Initialize a temp variable with the address of the above-created node.
- Run a while loop till the priority queue size is greater than 0.
- Store the topmost element of the queue into a variable, say p.
- Now remove the top element from the priority queue.
- Attach the node p at the end of our new list by doing temp->next = p.
- Now advance the temp variable by one node i.e, temp = temp->next.
- If the node after p is not NULL, push the node after p into the priority queue.
- After the completion of the while loop, return head->next, as it will be the first node of our newly created linked list.
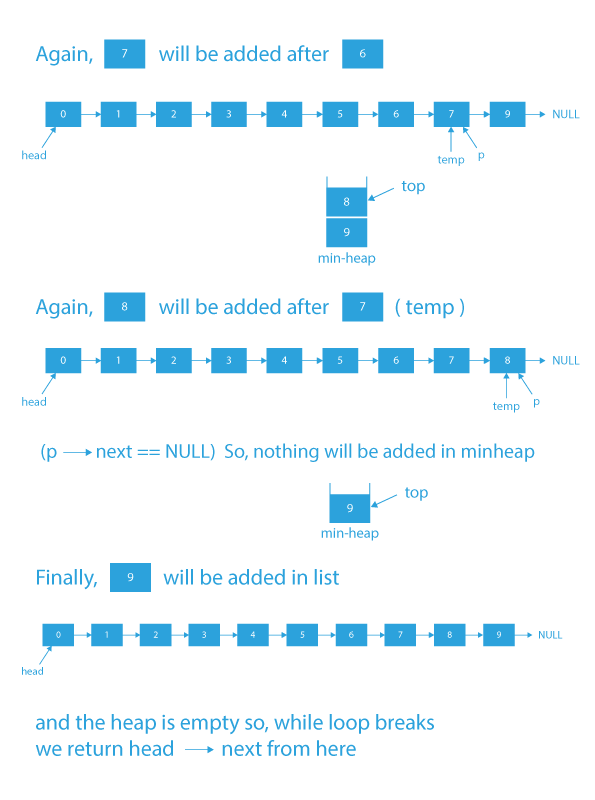
Dry Run of how to merge k sorted lists using heap
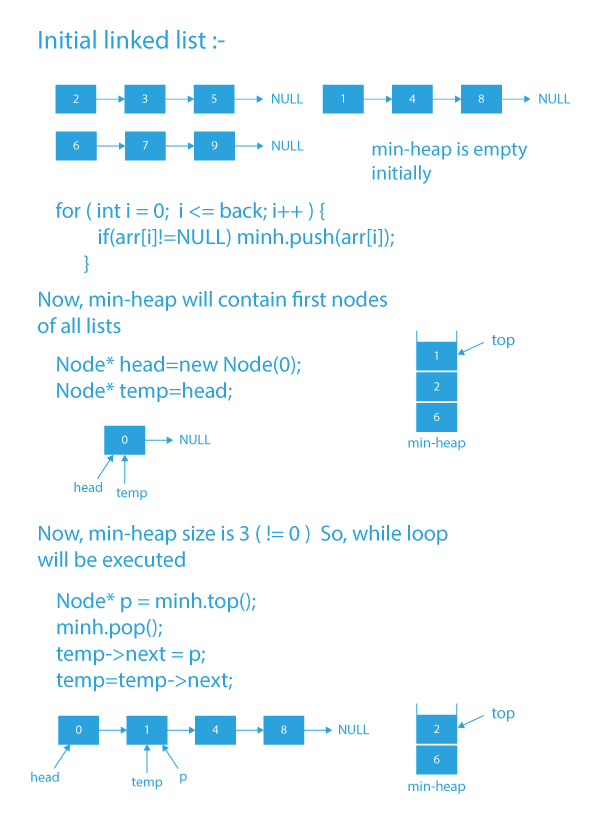
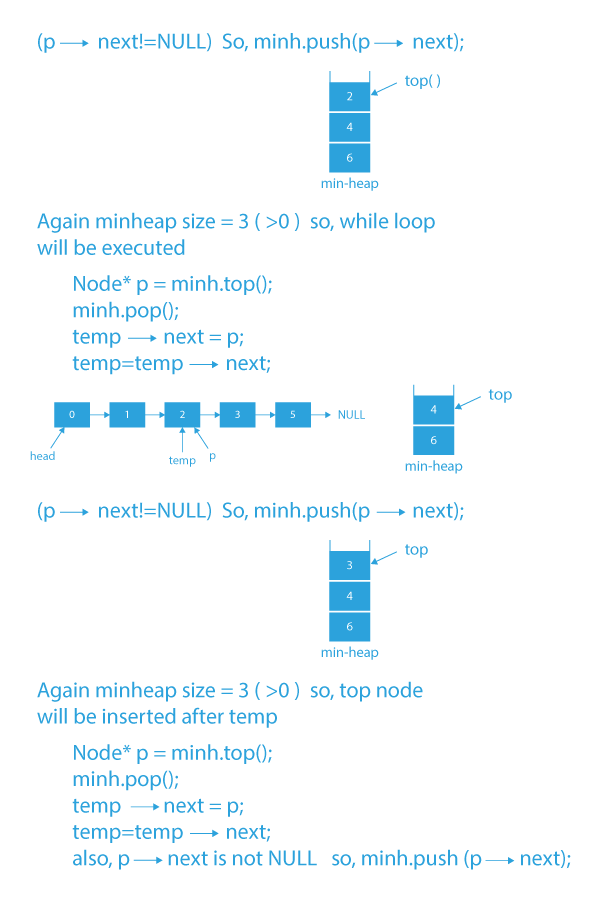
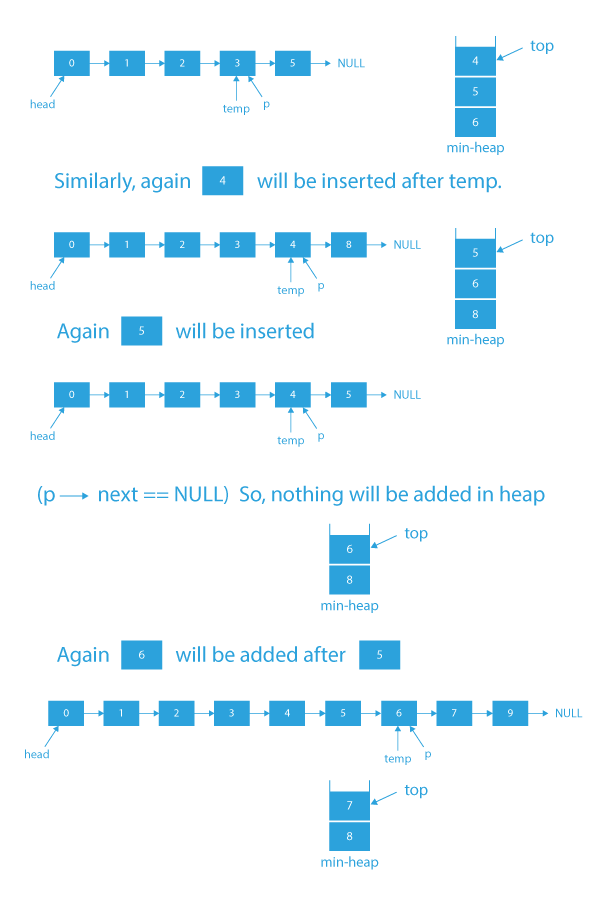
Code Implementation of how to merge k sorted lists using heap
#include<bits/stdc++.h>
using namespace std;
// class with constructor for a node of Linked list
class Node {
public:
int data;
Node* next;
// constructor
Node(int x){
data = x;
next = NULL;
}
};
// This function prints data of the linked list
void print(Node* head)
{
Node* curr = head;
while (curr != NULL) {
cout << curr->data << " -> ";
curr = curr->next;
}
cout<<"NULL";
}
// this is the comparator function for the priority queue to
// make it behave as a min-heap
struct compare
{
bool operator()(Node* &a,Node* &b)
{
return a->data>b->data;
}
};
// This function merges 'K' sorted lists into one sorted list
Node* mergeKLists(Node* arr[], int back)
{
priority_queue<Node*,vector<Node*>,compare>minh;
for(int i=0;i<=back;i++)
{
if(arr[i]!=NULL) minh.push(arr[i]);
}
Node* head=new Node(0);
Node* temp=head;
while(minh.size()>0)
{
Node* p = minh.top();
minh.pop();
temp->next = p;
temp=temp->next;
if(p->next!=NULL) minh.push(p->next);
}
return head->next;
}
// main function
int main()
{
Node * arr[3];
Node *head = new Node(2);
head->next = new Node(3);
head->next->next = new Node(5);
Node *h2 = new Node(1);
h2->next = new Node(4);
h2->next->next = new Node(8);
Node *h3 = new Node(6);
h3->next = new Node(7);
h3->next->next = new Node(9);
arr[0] = head;
arr[1] = h2;
arr[2] = h3;
cout<<"Final resultant merged linked list"<<endl;
print(mergeKLists(arr,2));
return 0;
}
import java.util.*;
class Node
{
int data;
Node next;
Node(int key)
{
data = key;
next = null;
}
}
class NodeComparator implements Comparator<node> {
public int compare(Node k1, Node k2)
{
if (k1.data > k2.data)
return 1;
else if (k1.data < k2.data)
return -1;
return 0;
}
}
class MergeKSorted
{
static Node mergeKList(Node[] arr, int K)
{
/* Priority_queue 'queue' implemented as min heap
with the help of 'compare' function */
PriorityQueue<node> queue
= new PriorityQueue<>(new NodeComparator());
Node at[] = new Node[K];
Node head = new Node(0);
Node last = head;
// Push the head nodes of all the k lists in 'queue'
for (int i = 0; i < K; i++) {
if (arr[i] != null) {
queue.add(arr[i]);
}
}
// Handles the case when k = 0 or lists have no elements in them
if (queue.isEmpty())
return null;
while (!queue.isEmpty())
{
Node curr = queue.poll();
last.next = curr;
last = last.next;
if (curr.next != null)
{
queue.add(curr.next);
}
}
return head.next;
}
public static void printList(Node node)
{
while (node != null) {
System.out.print(node.data + " ");
node = node.next;
}
}
public static void main(String[] args)
{
int N = 4;
// array to store head of linkedlist
Node[] a = new Node[N];
// Linkedlist1
Node head1 = new Node(1);
a[0] = head1;
head1.next = new Node(2);
head1.next.next = new Node(3);
// Limkedlist2
Node head2 = new Node(4);
a[1] = head2;
head2.next = new Node(5);
// Linkedlist3
Node head3 = new Node(5);
a[2] = head3;
head3.next = new Node(6);
// Linkedlist4
Node head4 = new Node(7);
a[3] = head4;
head4.next = new Node(8);
Node res = mergeKList(a, N);
if (res != null)
printList(res);
System.out.println();
}
}
import heapq
from heapq import heappop, heappush
# A Linked List Node
class Node:
def __init__(self, data, next=None):
self.data = data
self.next = next
# Override the `__lt__()` function to make `Node` class work with min-heap
def __lt__(self, other):
return self.data < other.data
# Utility function to print contents of a linked list
def printList(node):
while node:
print(node.data, end=' ')
node = node.next
# The main function to merge given `k` sorted linked lists.
# It takes a list of lists `list` of size `k` and generates the sorted output
def mergeKLists(lists):
# create a min-heap using the first node of each list
pq = [x for x in lists]
heapq.heapify(pq)
# take two pointers, head and tail, where the head points to the first node
# of the output list and tail points to its last node
head = last = None
# run till min-heap is empty
while pq:
# extract the minimum node from the min-heap
min = heappop(pq)
# add the minimum node to the output list
if head is None:
head = min
last = min
else:
last.next = min
last = min
# take the next node from the "same" list and insert it into the min-heap
if min.next:
heappush(pq, min.next)
# return head node of the merged list
return head
if __name__ == '__main__':
# total number of linked lists
k = 3
# a list to store the head nodes of the linked lists
lists = [None] * k
lists[0] = Node(2)
lists[0].next = Node(3)
lists[0].next.next = Node(5)
lists[1] = Node(1)
lists[1].next = Node(4)
lists[1].next.next = Node(8)
lists[2] = Node(6)
lists[2].next = Node(7)
lists[2].next.next = Node(9)
head = mergeKLists(lists)
printList(head)
Output
Final resultant merged linked list
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> NULLTime Complexity of how to merge k sorted lists using heap : O(NKlog(K)), N is the number of nodes in the list, and K is the total number of lists.
Conclusion
This blog tried to explain the merge k sorted lists using heap This problem tests a candidate’s problem-solving skills and his or her grasp on the concepts of linked list and heap. We highly encourage you to have a good grasp of major data structures. If you want to practice more questions on linked lists, feel free to solve them at Prepbytes Linked List.
FAQs related to how to merge k sorted lists using heap
1. What is the time complexity of merging two sorted lists?
The complexity is O(m log n). There are m iterations of the loop. Each insertion into a sorted array is an O(log n) operation. Therefore the overall complexity is O (m log n).
2. What is the algorithm for merge sort?
The Merge Sort algorithm is a sorting algorithm that is based on the Divide and Conquers paradigm. In this algorithm, the array is initially divided into two equal halves and then they are combined in a sorted manner.


