Last Updated on November 30, 2022 by Prepbytes

In this article, we will discuss one of the famous questions of linked lists “Point arbit pointer to greatest value right-side node in a linked list”. Having practice questions like “Point arbit pointer to greatest value right-side node in a linked list” will make your data structures like linked list strong. Now let’s go to our topic “Point arbit pointer to greatest value right-side node in a linked list” to understand it in detail.
How to point arbit pointer to greatest value right-side node in a linked list
Given a linked list in which each node will have an extra arbitrary pointer pointing to NULL initially. We need to make that arbitrary pointer point to the greatest valued node on the right side of that node.
The problem statement is quite straightforward; we will be given a singly linked list in which, apart from the next pointer, we will also have an arbit pointer which will be NULL initially, and we need to make that arbit pointer point to the greatest value in the right part of the list.
Let’s try to understand the problem with the help of examples.
Let the input given to us be:
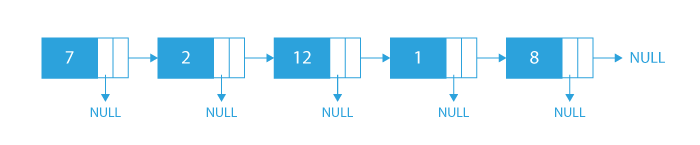
- For each node, we need to find the biggest valued node in its right and attach its arbit pointer to the biggest node.
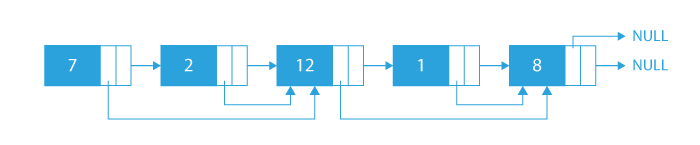
- For nodes ‘7’ and ‘2’, the biggest value in their right is node ‘12’ so, we will make the arbit pointer of both the nodes point to node with value ‘12’.
- Similarly, for nodes ‘12’ and ‘1’, the biggest value in their right is node ‘8’ so, we will make the arbit pointer of both the nodes point to node with value ‘8’.
- And for node ‘8’, there is no node on its right side. So, its arbit pointer remains NULL.
So, the output will be:
Taking another example, if the given linked list is:
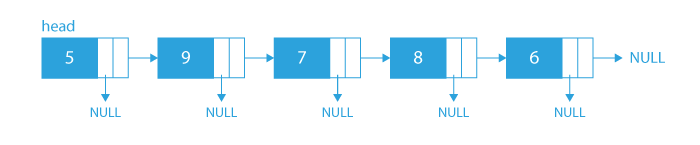
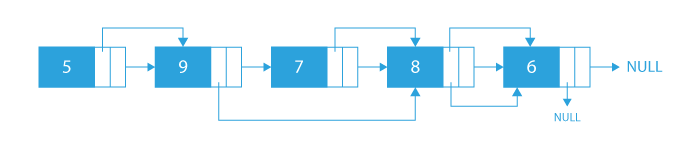
- Now, in this case, for ‘5’ the biggest valued node on the right side of ‘5’ is the node with value ‘9’, so we will make arbit pointer of node ‘5’ point to node with value ‘9’.
- Similarly, for each node, we will make their arbit pointer point to the greatest valued node on their right side. Arbit of ‘9’ will point to ‘8’, arbit of ‘7’ will point to ‘8’, arbit of ‘8’ wil point to ‘6’ and arbit of ‘6’ will point to NULL as there are no nodes on right size of the node with value ‘6’.
So, our output will be:
Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Let’s move to the approach section.
Approach 1
Our approach will be simple:
- We will keep two iterators for iterating the list.
- Once we fix the first iterator, we will move the second iterator from first iterators next till the end of the list to find the maximum valued node.
- After that, we will connect the arbit pointer of the node pointed by the first iterator to the maximum valued node found by the second iterator.
- We repeat the same process for each node.
Time Complexity: O(n2), n is the number of nodes in the list.
Space Complexity: O(1), no extra space used.
The above approach seems trivial but, it has a huge time complexity of O(n2). Can we reduce that and make our code more efficient in terms of time?
- The answer is yes, and let us see the way to do that in the below approach.
Let’s move to a more optimized approach.
Approach 2
- Every time, to find the greatest valued node corresponding to a node, we need to look right in the list (iterate the list from node’s next to the end of the list), to make things simpler, we can think of iterating the list from end to start.
- We cannot iterate the list backward so, we need to reverse the list first, if we want to do so.
- Now, after reversing the list, we only need to keep the address of the max-valued node in a variable and update it on each iteration.
- On reaching each node, we will have a max valued node in its left, stored in a variable, and we just need to connect the node’s arbit pointer to the stored node.
- Finally, after connecting the arbit pointers of each node of the list, we need to reverse the list again to keep it to its original form.
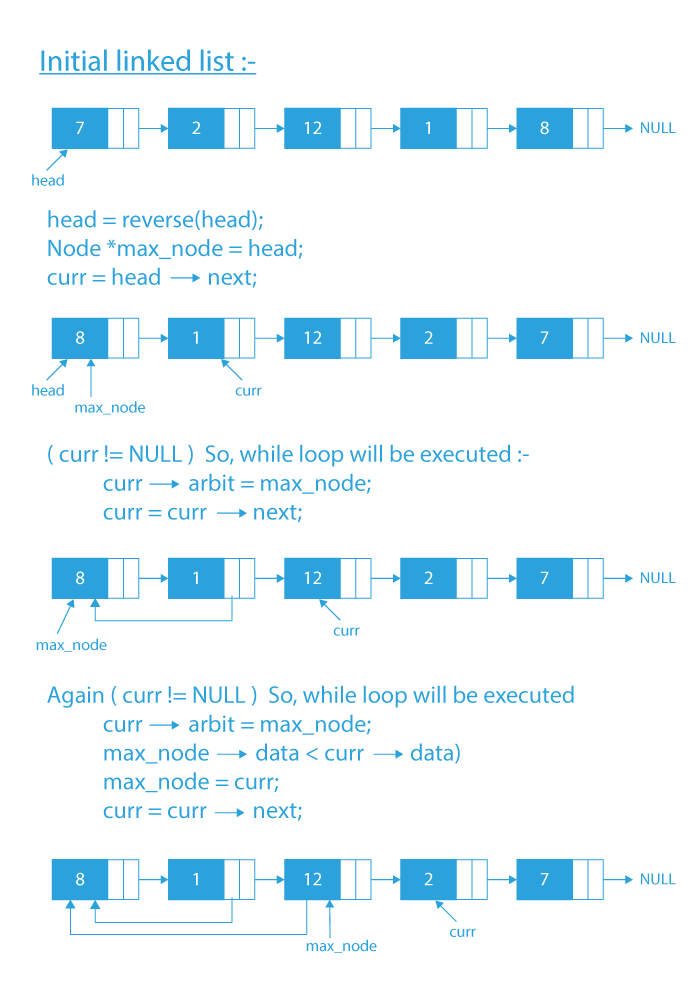
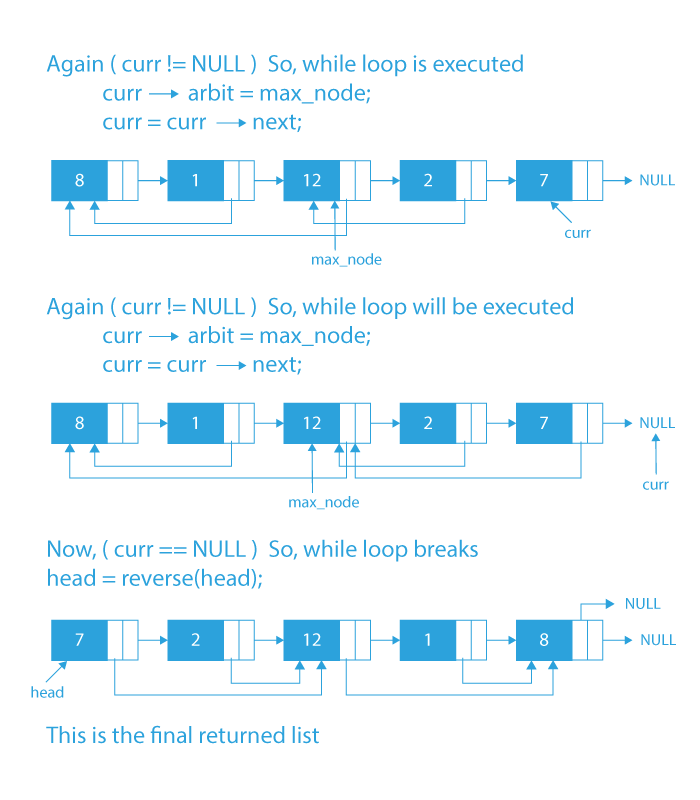
Algorithm
- First, reverse the given linked list.
- Initialize a pointer max_node with the first node in the reversed list.
- Initialize a pointer curr with the second node in the reversed list.
- Run a while loop till curr is not NULL.
- Update arbit pointer of curr node with max_node.
- If curr data is greater than max_node data, then update max_node with curr.
- Advance curr by one node.
- Again reverse the list and return it.
Dry Run
Code Implementation
#include<bits stdc++.h="">
using namespace std;
// class with constructor for a node of Linked list
class Node {
public:
int data;
Node* next,*arbit;
// constructor
Node(int x){
data = x;
next = NULL;
arbit = NULL;
}
};
// This function reverses the given list and returns
// the head of the reversed list
Node* reverse(Node *head)
{
Node *prev = NULL, *current = head, *next;
while (current != NULL)
{
next = current->next;
current->next = prev;
prev = current;
current = next;
}
return prev;
}
// This function assigns the correct node address to each node’s
// arbit pointer
Node* solve(Node *head)
{
// first reverse the given list
head = reverse(head);
// Initialize a pointer with first node of
// reversed list
Node *max_node = head;
// Initialize a pointer to traverse the list
Node *curr = head->next;
while (curr != NULL)
{
// connect the curr pointer with max_node
// pointer which will have the maximum valued
// node's value in left
curr->arbit = max_node;
// If this node is greater than max_node
// then update the max_node
if (max_node->data < curr->data)
max_node = curr;
// advance curr to move to next node
curr = curr->next;
}
// again reverse the list to bring it again
// to its original form
return reverse(head);
}
// this function will print value of each node's
// next node and arbit node
void checkValue(Node *head)
{
cout<<"node\tNext Pointer\tArbit Pointer\n";
while (head!=NULL)
{
cout << head->data << "\t\t";
if (head->next)
cout << head->next->data << "\t\t";
else cout << "NULL" << "\t\t";
if (head->arbit)
cout << head->arbit->data;
else cout << "NULL";
cout << endl;
head = head->next;
}
}
// main function
int main()
{
Node *head = new Node(7);
head->next = new Node(2);
head->next->next = new Node(12);
head->next->next->next = new Node(1);
head->next->next->next->next = new Node(8);
head = solve(head);
checkValue(head);
return 0;
}
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next, *arbit;
};
// This function populates arbit pointer in every
// node to the greatest value to its right.
void populateArbit(struct Node *head)
{
// using static maxNode to keep track of maximum
// orbit node address on right side
static struct Node *maxNode;
// if head is null simply return the list
if (head == NULL)
return;
/* if head->next is null it means we reached at
the last node just update the max and maxNode */
if (head->next == NULL)
{
maxNode = head;
return;
}
/* Calling the populateArbit to the next node */
populateArbit(head->next);
/* updating the arbit node of the current
node with the maximum value on the right side */
head->arbit = maxNode;
/* if current Node value id greater then
the previous right node then update it */
if (head->data > maxNode->data)
maxNode = head;
return;
}
// Utility function to print result linked list
void printNextArbitPointers(struct Node *node)
{
printf("Node\tNext Pointer\tArbit Pointer\n");
while (node!=NULL)
{
printf("%d\t\t",node->data);
if(node->next)
printf("%d \t\t",node->next->data);
else printf("\t\t","NULL");
if(node->arbit)
printf("%d ",node->arbit->data);
else printf("NULL");
printf("\n");
node = node->next;
}
}
/* Function to create a new node with given data */
struct Node *newNode(int data)
{
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node*));
new_node->data = data;
new_node->next = NULL;
return new_node;
}
/* Driver program to test above functions*/
int main()
{
struct Node *head = newNode(5);
head->next = newNode(10);
head->next->next = newNode(2);
head->next->next->next = newNode(3);
populateArbit(head);
printf("Resultant Linked List is: \n");
printNextArbitPointers(head);
return 0;
}
class PrepBytes
{
/* Link list node */
static class Node
{
int data;
Node next, arbit;
}
/* Function to reverse the linked list */
static Node reverse(Node head)
{
Node prev = null, current = head, next = null;
while (current != null)
{
next = current.next;
current.next = prev;
prev = current;
current = next;
}
return prev;
}
// This function populates arbit pointer in every
// node to the greatest value to its right.
static Node populateArbit(Node head)
{
// Reverse given linked list
head = reverse(head);
// Initialize pointer to maximum value node
Node max = head;
// Traverse the reversed list
Node temp = head.next;
while (temp != null)
{
// Connect max through arbit pointer
temp.arbit = max;
// Update max if required
if (max.data < temp.data)
max = temp;
// Move ahead in reversed list
temp = temp.next;
}
// Reverse modified linked list and return
// head.
return reverse(head);
}
// Utility function to print result linked list
static void printNextArbitPointers(Node node)
{
System.out.println("Node\tNext Pointer\tArbit Pointer");
while (node != null)
{
System.out.print(node.data + "\t\t");
if (node.next != null)
System.out.print(node.next.data + "\t\t");
else
System.out.print("NULL" +"\t\t");
if (node.arbit != null)
System.out.print(node.arbit.data);
else
System.out.print("NULL");
System.out.println();
node = node.next;
}
}
/* Function to create a new node with given data */
static Node newNode(int data)
{
Node new_node = new Node();
new_node.data = data;
new_node.next = null;
return new_node;
}
/* Driver code*/
public static void main(String[] args)
{
Node head = newNode(7);
head.next = newNode(2);
head.next.next = newNode(12);
head.next.next.next = newNode(1);
head.next.next.next.next = newNode(8);
head = populateArbit(head);
System.out.println("Resultant Linked List is: ");
printNextArbitPointers(head);
}
}
# Node class
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.arbit = None
# Function to reverse the linked list
def reverse(head):
prev = None
current = head
next = None
while (current != None):
next = current.next
current.next = prev
prev = current
current = next
return prev
# This function populates arbit pointer in every
# node to the greatest value to its right.
def populateArbit(head):
head = reverse(head)
max = head
temp = head.next
while (temp != None):
temp.arbit = max
if (max.data < temp.data):
max = temp
temp = temp.next
return reverse(head)
# Utility function to print result linked list
def printNextArbitPointers(node):
print("Node\tNext Pointer\tArbit Pointer\n")
while (node != None):
print( node.data , "\t\t",end = "")
if (node.next != None):
print( node.next.data , "\t\t",end = "")
else :
print( "None" , "\t\t",end = "")
if (node.arbit != None):
print( node.arbit.data,end = "")
else :
print( "None",end = "")
print("\n")
node = node.next
# Function to create a new node with given data
def newNode(data):
new_node = Node(0)
new_node.data = data
new_node.next = None
return new_node
head = newNode(7)
head.next = newNode(2)
head.next.next = newNode(12)
head.next.next.next = newNode(1)
head.next.next.next.next = newNode(8)
head = populateArbit(head)
print("Resultant Linked List is: \n")
printNextArbitPointers(head)
Output
| node | Next Pointer | Arbit Pointer |
|---|---|---|
| 7 | 2 | 12 |
| 2 | 12 | 12 |
| 12 | 1 | 8 |
| 1 | 8 | 8 |
| 8 | NULL | NULL |
Time Complexity: O(n), where n is the total number of nodes in the list
This blog have tried to explain how you can Point arbit pointer to greatest value right-side node in a linked list in the most optimal way. This is a good problem to strengthen your concepts in LinkedList. Our Expert Mentors have build one linked list questions list which will strengthen your data structures like linked list, you can checkout Prepbytes (Linked List) for practicing more questions in linked list.
FAQ
1. What pointer points to the next member of the list?
A linked list is a set of dynamically allocated nodes, arranged in such a way that each node contains one value and one pointer. The pointer always points to the next member of the list.
2. What are the 4 types of linked list?
Types of Linked List :
- Singly Linked List.
- Doubly Linked List.
- Circular Linked List.
- Circular Doubly List.


