Last Updated on November 25, 2022 by Prepbytes

A linked list is a linear data structure. In the linked list elements are not stored continuously but randomly. It is a vital topic from the placement point of view, and there are several problems related to it. In this blog, we will learn to rearrange a linked list such that all even and odd positioned nodes are together
How to rearrange a linked list such that all even and odd positioned nodes are together
In this problem, we will be given a linked list, and we need to rearrange the nodes such that the nodes present at odd positions and the nodes present at even positions are together.
To understand this problem statement, let us take examples.
If the given linked list is:

then according to the problem statement:
- Starting the counting from 1, the nodes at odd positions are 3,18, and 5.
- Nodes at even positions are 1 and 12.
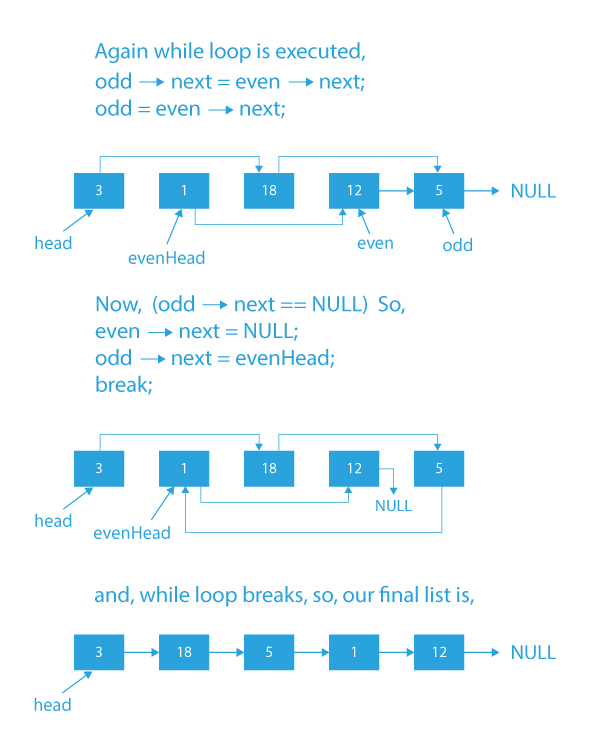
- So, after rearrangement, the resultant list will be:

Let us take another example:
If the linked list is 4→1→10→42→5→NULL.
- Starting the counting from 1, the nodes at odd positions are 4,10, and 5.
- Nodes at even positions are 1 and 42.
- So, after rearrangement, the resultant list will be 4→10→5→1→42→NULL.
Now, I think the problem statement is clear, so let’s see how we can approach it. Any ideas?
- If not, it’s okay; we will see in the next section how we can approach it.
Let’s move to the approach section.
Approach of rearrange a linked list such that all even and odd positioned nodes are together
- We will use two pointers, where at first, we will initialize these pointers with the address of the first and the second node of the linked list.
- Now, we will iterate the list from the first node to the last node.
- While iterating, we will connect the node pointed by each pointer to the node next to the adjacent node in its right.
- This will ensure that all odd and even positioned nodes are with each other, respectively.
- At last, we need to connect the tail of the odd list with the head of the even list.
- Finally, after all the above steps, we will have our rearranged linked list with all the even and the odd-positioned nodes together.
The approach is discussed in more depth in the algorithm section.
Algorithm of rearrange a linked list such that all even and odd positioned nodes are together
1) We will return NULL if the head is NULL, i.e., the input list is empty.
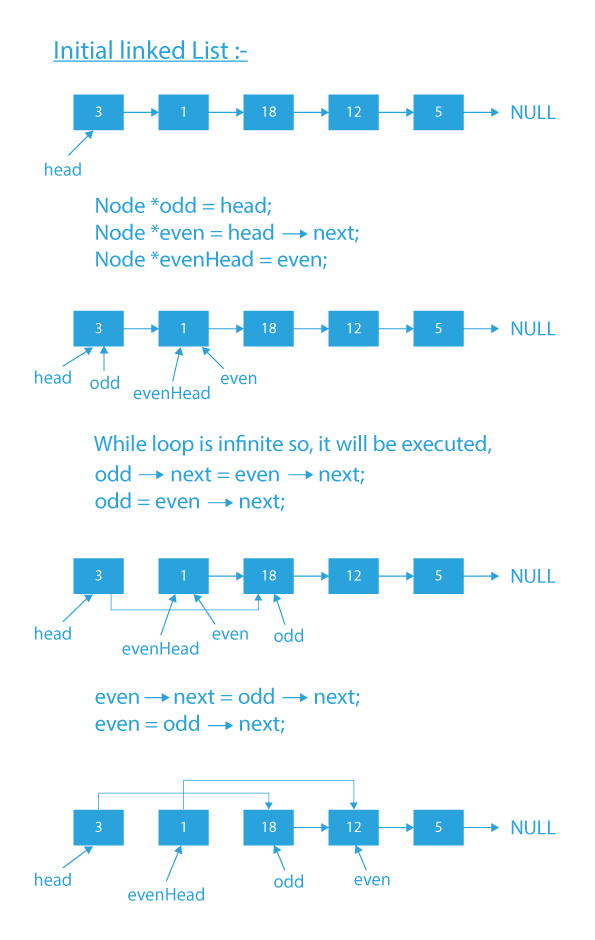
2) Initialize two pointers odd and even with the first and the second node of the list, respectively.
3) Initialize a pointer evenHead with the second node.
4) Run an infinite while loop and inside it:
- If any one of odd, even, or even→next is NULL (i.e., we have reached the end of the list, so we will connect the last node of odd list to the first node of the even list), then attach the tail of odd to the head of even and break from the loop.
- Connect odd to the node next to even and update odd with this node.
- If the node next to odd is NULL (i.e., no node after the current odd node), then update the next of even as NULL and attach the tail of odd to the head of even and break from the loop.
- Connect even to the node next to odd and update even with this node.
5) Return head at last from the function.
Dry Run of rearrange a linked list such that all even and odd positioned nodes are together
Code Implementation of rearrange a linked list such that all even and odd positioned nodes are together
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
// A utility function to create a new node
struct Node* newNode(int key)
{
struct Node *temp = (struct Node *) malloc(sizeof(struct Node));
temp->data = key;
temp->next = NULL;
return temp;
}
// Rearranges given linked list such that all even
// positioned nodes are before odd positioned.
// Returns new head of linked List.
struct Node *rearrangeEvenOdd(struct Node *head)
{
// Corner case
if (head == NULL)
return NULL;
// Initialize first nodes of even and
// odd lists
struct Node *odd = head;
struct Node *even = head->next;
// Remember the first node of even list so
// that we can connect the even list at the
// end of odd list.
struct Node *evenFirst = even;
while (1)
{
// If there are no more nodes, then connect
// first node of even list to the last node
// of odd list
if (!odd || !even || !(even->next))
{
odd->next = evenFirst;
break;
}
// Connecting odd nodes
odd->next = even->next;
odd = even->next;
// If there are NO more even nodes after
// current odd.
if (odd->next == NULL)
{
even->next = NULL;
odd->next = evenFirst;
break;
}
// Connecting even nodes
even->next = odd->next;
even = odd->next;
}
return head;
}
// A utility function to print a linked list
void printlist(struct Node * node)
{
while (node != NULL)
{
printf("%d->",node->data);
node = node->next;
}
printf("NULL\n");
}
// Driver code
int main(void)
{
struct Node *head = newNode(6);
head->next = newNode(7);
head->next->next = newNode(8);
head->next->next->next = newNode(9);
head->next->next->next->next = newNode(10);
printf("Given Linked List\n");
printlist(head);
head = rearrangeEvenOdd(head);
printf("\nModified Linked List\n");
printlist(head);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
class Node{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
// Using this function we will print the linked list
void printList(Node *head)
{
if (!head)
return;
while (head->next != NULL)
{
cout << head->data << ",";
head = head->next;
}
cout << head->data << endl;
}
// Function to rearrange the linked list
Node *rearrangeEvenOdd(Node *head)
{
// Empty list condition
if (head == NULL)
return NULL;
Node *odd = head;
Node *even = head->next;
// first node of even list
Node *evenHead = even;
while (1)
{
// If we have reached end of the list
// then, connect last node of odd list
// to the first node of even list
if (!odd || !even || !(even->next))
{
odd->next = evenHead;
break;
}
odd->next = even->next;
odd = even->next;
// No nodes after current odd node
if (odd->next == NULL)
{
even->next = NULL;
odd->next = evenHead;
break;
}
even->next = odd->next;
even = odd->next;
}
return head;
}
int main(void){
Node* head = NULL;
head = new Node(3);
head->next = new Node(1);
head->next->next = new Node(18);
head->next->next->next = new Node(12);
head->next->next->next->next = new Node(5);
cout<<"Original linked list without rearrangement: "<<endl;
printList(head);
Node *tmp = rearrangeEvenOdd(head);
cout<<"Linked list after rearrangement: "<<endl;
printList(tmp);
return 0;
}
class Rearrange
{
static class Node
{
int data;
Node next;
}
static Node newNode(int key)
{
Node temp = new Node();
temp.data = key;
temp.next = null;
return temp;
}
/* Rearranges given linked list such that all even positioned
nodes are before odd positioned returns new head of linked List.*/
static Node rearrangeEvenOdd(Node head)
{
// Corner case
if (head == null)
return null;
// Initialize first nodes of even and odd lists
Node odd = head;
Node even = head.next;
/* Remember the first node of even list so
that we can connect the even list at the end of odd list.*/
Node evenFirst = even;
while (1 == 1)
{
/* If there are no more nodes,
then connect first node of even
list to the last node of odd list*/
if (odd == null || even == null ||(even.next) == null)
{
odd.next = evenFirst;
break;
}
// Connecting odd nodes
odd.next = even.next;
odd = even.next;
// If there are NO more even nodes after current odd.
if (odd.next == null)
{
even.next = null;
odd.next = evenFirst;
break;
}
// Connecting even nodes
even.next = odd.next;
even = odd.next;
}
return head;
}
static void printlist(Node node)
{
while (node != null)
{
System.out.print(node.data + "->");
node = node.next;
}
System.out.println("NULL") ;
}
// Driver code
public static void main(String[] args)
{
Node head = newNode(1);
head.next = newNode(2);
head.next.next = newNode(3);
head.next.next.next = newNode(4);
head.next.next.next.next = newNode(5);
System.out.println("Given Linked List");
printlist(head);
head = rearrangeEvenOdd(head);
System.out.println("Modified Linked List");
printlist(head);
}
}
class Node:
def __init__(self, d):
self.data = d
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def newNode(self, key):
temp = Node(key)
self.next = None
return temp
def rearrangeEvenOdd(self, head):
if (self.head == None):
return None
odd = self.head
even = self.head.next
evenFirst = even
while (1 == 1):
if (odd == None or even == None or
(even.next) == None):
odd.next = evenFirst
break
odd.next = even.next
odd = even.next
if (odd.next == None):
even.next = None
odd.next = evenFirst
break
even.next = odd.next
even = odd.next
return head
def printlist(self, node):
while (node != None):
print(node.data, end = "")
print("->", end = "")
node = node.next
print ("NULL")
def push(self, new_data):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node
ll = LinkedList()
ll.push(5)
ll.push(12)
ll.push(18)
ll.push(1)
ll.push(3)
print ("Given Linked List")
ll.printlist(ll.head)
start = ll.rearrangeEvenOdd(ll.head)
print ("Modified Linked List")
ll.printlist(start)
Output
Original linked list without rearrangement:
3,1,18,12,5
Linked list after rearrangement:
3,18,5,1,12
Time Complexity of rearrange a linked list such that all even and odd positioned nodes are together: O(n), where n is the total number of nodes in the list.
So, in this blog, we have tried to explain how we can rearrange a linked list such that all even and odd positioned nodes are together most optimally. Practicing a bunch of questions is not enough in this competitive world. So go check out where you stand among your peers by taking our Linked List.and see which areas need improvement
## FAQs
**1. What is the key difference between a singly linked list and a doubly-linked list?**
A singly-linked list is unidirectional, which means that the node of a singly-linked list contains the pointer to its next node only. In contrast, a doubly-linked list is bidirectional, and its node contains the pointer to its next and previous nodes.
**2. How do you sort a linked list?**
Below is a simple insertion sort algorithm for a linked list.
– Create an empty sorted (or result) list.
– Traverse the given list, and do the following for every node.
– Insert the current node in a sorted way in a sorted or result list.
– Change the head of the given linked list to the head of the sorted (or result) list.
**3. Which of the following method is used for sorting in merge sort?**
The divide and conquer technique is used for merge sort.


