Rotate a Linked List

Last Updated on November 27, 2023 by Ankit Kochar

Manipulating linked lists is a core aspect of data structures and algorithms in programming. Rotating a linked list involves rearranging its elements by shifting nodes to a specified number of positions. Understanding how to perform this operation is crucial for various applications, such as in optimizing memory usage or solving specific programming problems efficiently. This article aims to explore the concept of rotating a linked list, delve into different approaches for rotation, and provide insights into the algorithms and techniques involved in accomplishing this task.

How to Rotate a Linked List?

In this question, we are given a singly linked list and an integer X. We have to rotate the list counter-clockwise by X nodes.

Note: X is smaller than the count of nodes in the linked list.

Let’s try to understand the problem statement with the help of an example.

Suppose the given linked list 1 → 2 → 5 → 10 – 12 → 13, and the value of X is 4. Now, we have to rotate the given list counter-clockwise by X.

Here, rotating counter-clockwise a linked list by X means that the first X nodes of the linked list will be removed from the start and get appended to the end of the list.

In the given list, the first 4 nodes are 1 → 2 → 5 → 10. Now, these 4 elements will get appended to the end of the list. So, the final list will be:
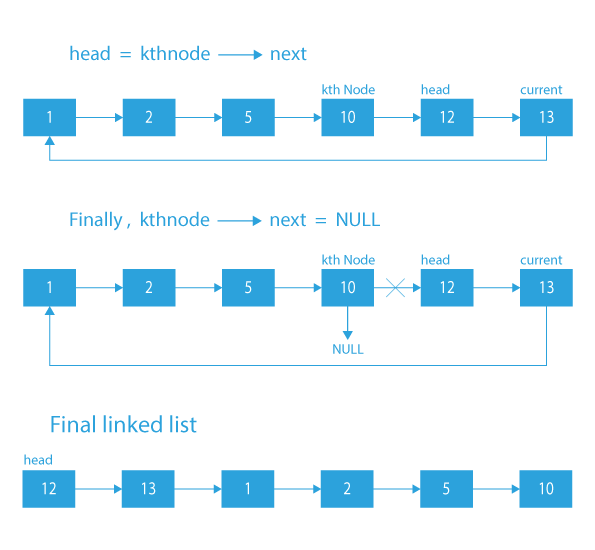
12 → 13 → 1 → 2 → 5 → 10.

In this way, we are rotating the given first X nodes counter-clockwise.

Input :

Output :

Explanation : As the value of X is 4, so the first 4 nodes have been removed from the beginning of the linked list and appended at the end of the linked list.

Now, I think from the above example, it is clear what we have to do in this problem. So let’s move to approach.

Before directly jumping to approach in the next section, just try to think how will approach this problem?

It’s okay if your solution is not the best-optimized solution, we will try to optimize it together.

This question is not a very complex one. We are going to make use of linked list traversal in this question. Let us have a glance at the approach.

Approach and Algorithm of rotate a linked list

The approach is going to be pretty simple.
Let us first think about what we need to perform the required task of rotating the list counter-clockwise by X nodes.

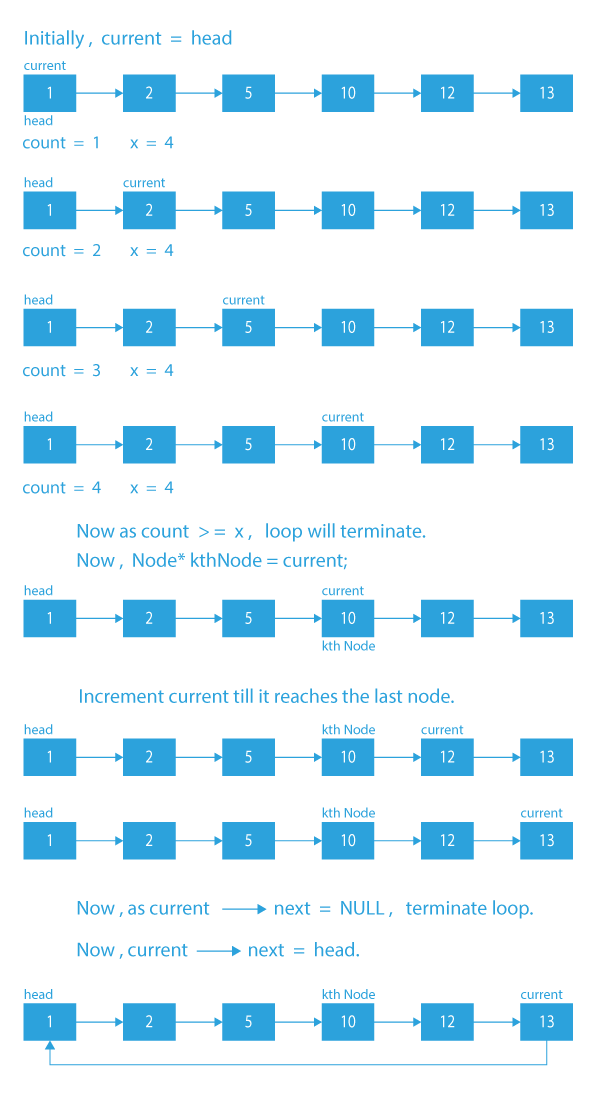
• For linked list rotation, we have to change the next of X^th node to NULL, next of the last node to the head node, and finally, make the head point to the (X+1)^th node.
• So, we need X^th node, (X+1)^th node and the last node.

To acheive the above objective of rotation:

• We will traverse through the list and stop at the X^th node.
• We will store the pointer to the X^th node.
• The (X+1)^th node can be reached using the next of X^th node. Now, we will keep traversing the list till the last node, and change the pointers as stated below:
  • Change the next of X^th node to NULL
  • Next of the last node to the head node.
  • And finally, make the head point to the (X+1)^th node.

Dry Run of rotate a linked list

Code Implementation of rotate a linked list

#include <stdio.h>
#include <stdlib.h>
 
/* Link list node */
struct Node {
    int data;
    struct Node* next;
};
 
void rotate(struct Node** head_ref, int k)
{
    if (k == 0)
        return;
 
    struct Node* current = *head_ref;
 
    int count = 1;
    while (count < k && current != NULL) {
        current = current->next;
        count++;
    }
 
    if (current == NULL)
        return;
 
    struct Node* kthNode = current;
 
    while (current->next != NULL)
        current = current->next;
 
    current->next = *head_ref;
 
    *head_ref = kthNode->next;
 
    kthNode->next = NULL;
}
 
void push(struct Node** head_ref, int new_data)
{
    /* allocate node */
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
 
    /* put in the data  */
    new_node->data = new_data;
 
    /* link the old list off the new node */
    new_node->next = (*head_ref);
 
    /* move the head to point to the new node */
    (*head_ref) = new_node;
}
 
void printList(struct Node* node)
{
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}
int main(void)
{
    struct Node* head = NULL;
 
    for (int i = 60; i > 0; i -= 10)
        push(&head, i);
 
    printf("Given linked list \n");
    printList(head);
    rotate(&head, 4);
 
    printf("\nRotated Linked list \n");
    printList(head);
 
    return (0);
}

#include <bits stdc++.h="">
using namespace std;

class Node {
public:
    int data;
    Node* next;
};

void rotate(Node** head_ref, int k)
{
    if (k == 0)
        return;

    Node* current = *head_ref;

    int count = 1;
    while (count < k && current != NULL) {
        current = current->next;
        count++;
    }

    if (current == NULL)
        return;

    Node* kthNode = current;

    while (current->next != NULL)
        current = current->next;
 
    current->next = *head_ref;

    *head_ref = kthNode->next;

    kthNode->next = NULL;
}

void push(Node** head_ref, int new_data)
{

    Node* new_node = new Node();

    new_node->data = new_data;

    new_node->next = (*head_ref);

    (*head_ref) = new_node;
}

void printList(Node* node)
{
    while (node != NULL) {
        cout << node->data << " ";
        node = node->next;
    }
}

int main(void)
{

    Node* head = NULL;

       push(&head, 13);
       push(&head,12);
       push(&head,10);
       push(&head,5);
       push(&head,2);
       push(&head,1);
     
 
    cout << "Given linked list \n";
    printList(head);
    rotate(&head, 4);
 
    cout << "\nRotated Linked list \n";
    printList(head);
 
    return (0);
}

public class LinkedList {
    Node head; 
    
    class Node {
        int data;
        Node next;
        Node(int d)
        {
            data = d;
            next = null;
        }
    }

    void rotate(int k)
    {
        if (k == 0)
            return;

        Node current = head;

        int count = 1;
        while (count < k && current != null) {
            current = current.next;
            count++;
        }

        if (current == null)
            return;

        Node kthNode = current;

        while (current.next != null)
            current = current.next;


        current.next = head;

        head = kthNode.next;

        kthNode.next = null;
    }

    void push(int new_data)
    {

        Node new_node = new Node(new_data);

        new_node.next = head;

        head = new_node;
    }

    void printList()
    {
        Node temp = head;
        while (temp != null) {
            System.out.print(temp.data + " ");
            temp = temp.next;
        }
        System.out.println();
    }

    public static void main(String args[])
    {
        LinkedList llist = new LinkedList();

        
            llist.push(13);
            llist.push(12);
            llist.push(10);
            llist.push(5);
            llist.push(2);
            llist.push(1);
            

        System.out.println("Given list");
        llist.printList();

        llist.rotate(4);

        System.out.println("Rotated Linked List");
        llist.printList();
    }
} 

class Node:

	def __init__(self, data):
		self.data = data
		self.next = None

class LinkedList:

	def __init__(self):
		self.head = None

	def push(self, new_data):

		new_node = Node(new_data)
		new_node.next = self.head
		self.head = new_node

	def printList(self):
		temp = self.head
		while(temp):
			print(temp.data, end=" ")
			temp = temp.next

	def rotate(self, k):
		if k == 0:
			return
		
		current = self.head
		count = 1

		while(count <k and current is not None):
			current = current.next
			count += 1

		if current is None:
			return

		kthNode = current
	
		while(current.next is not None):
			current = current.next

		current.next = self.head
		self.head = kthNode.next
		kthNode.next = None



llist = LinkedList()

llist.push(13)
llist.push(12)
llist.push(10)
llist.push(5)
llist.push(2)
llist.push(1)

print("Given linked list")
llist.printList()
llist.rotate(4)

print("\nRotated Linked list")
llist.printList()

Output
Given linked list: 1 2 5 10 12 13
Rotated Linked list: 12 13 1 2 5 10 

Time Complexity rotate a linked list: O(n), as list traversal is needed.

Conclusion
Rotating a linked list is a fundamental operation that finds utility in various programming scenarios. The methods and algorithms discussed in this article offer diverse approaches to efficiently perform rotations, catering to different requirements and complexities. Understanding these techniques equips programmers with valuable tools to manipulate linked lists effectively, facilitating optimized solutions for problems that demand reordering elements within these data structures. Mastering linked list rotation is not only essential for algorithmic problem-solving but also for enhancing one’s proficiency in data structure manipulation and algorithm design.

By comprehending the nuances of linked list rotation and employing the appropriate algorithms, developers can optimize code efficiency, streamline solutions, and harness the full potential of linked lists in programming applications.

FAQs related to Rotate Linked list

Here are some FAQs related to Rotate Linked List.

1. What does rotating a linked list mean?
Rotating a linked list involves repositioning its elements by moving nodes a specified number of places either to the left or right. It essentially changes the order of the elements in the list while maintaining its structure.

2. How is the rotation direction determined in a linked list?
The direction of rotation in a linked list, whether left or right, depends on the problem statement or the desired outcome. For instance, rotating a list left means moving nodes from the beginning to the end, while a right rotation involves moving nodes from the end to the beginning.

3. What are the different approaches to rotate a linked list?
Iterative Method: Involves traversing the list to find the new head and tail nodes after rotation.
Using k-th Node: Identifying the k-th node from the beginning and making it the new head after rotation.
Reversal Technique: Combining reversal and node manipulation to achieve rotation efficiently.

4. How efficient are the rotation algorithms for large linked lists?
The efficiency of rotation algorithms depends on the approach used. Some techniques might involve traversing the list multiple times, impacting performance for large lists. However, certain methods like using the k-th node or the reversal technique can offer better efficiency in terms of time complexity.

5. Are there any considerations while implementing linked list rotation?
It’s essential to handle edge cases such as empty lists, rotations beyond the list length, or handling rotations when the number of positions is greater than the list size. Additionally, maintaining the pointers correctly during rotation to avoid memory leaks or dangling pointers is crucial.