Write a C function to print the middle of a linked list

Last Updated on December 1, 2022 by Prepbytes

This blog will discuss how to make a C function to print the middle of a linked list. Linked list is one of the most interesting topics when you start practicing data structures. This blog is having both a naive and optimal approach to make a c function to print the middle of a linked list. Let’s discuss how to make a C function to print the middle of a linked list

How To Make C Function To Print The Middle Of A Linked List

In this problem, we are given a linked list. We have to find the middle of the linked list.

Let’s suppose we have a linked list whose length is L, then the middle of the linked list will be the (L/2)^th node of the linked list.
Suppose the given list is 5 → 10 → 3 → 4 → 8.

• The length of this linked list is 5.
• So, (5/2) = 2^nd node will be the middle node of the linked list.
• The middle of the linked list will be the node at 2^nd position, which is 3, considering 0 based indexing.

Taking another example, let’s assume that the given linked list 1 → 3 → 5 → 7 → 9 → 11.

• In this case, the length of this linked list is 6. So, (6/2) = 3^rd node will be the middle node of the linked list.
• The middle of the linked list will be the node at 3^rd position, which is 7, considering 0 based indexing.

Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.
Before moving to the further to approach section, try to think about how you can approach this problem.

• If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.

There are two solutions to this problem. One is the naive one and the second one is the optimal solution. The naive solution requires two traversals of the list, while the optimal solution only requires a single traversal of the linked list.

Let’s have a glance at the naive approach and then see what we can do to optimize it.

Approach and Algorithm (Naive approach) To Make C Function To Print The Middle Of A Linked List

Here, in this approach, we first calculate the length of the list. Let the length be len.

• Now, we traverse till the (len/2)^th node and print it as it is obviously the middle node of the list.

This is the naive approach to solve this problem, but as we are preparing for coding interviews of big companies, we should be familiar with techniques to find the middle node of the linked list without finding the length first.
The optimal solution requires a single traversal of the linked list and is the best way to find the middle of a linked list.

Time Complexity To Make C Function To Print The Middle Of A Linked List: O(N) – two traversals required.

Space Complexity To Make C Function To Print The Middle Of A Linked List: O(1), as only temporary variables are being created.

Now, let us discuss the approach in which we can find the middle of a linked list with a single traversal.

What if we start by taking two pointers, say slow and fast, and make both of them point to the head initially.

• Now, what will happen if we make the slow jump one place and the fast jump two places (fast moving with twice the speed of slow).
• If we notice carefully, by doing the above step, when the fast will reach the end of the list, the slow will be pointing to the middle of the list. With the help of this technique, we can reach the middle node of a linked list in a single pass.

Note: The reason why our slow pointer will be pointing to the middle of the linked list when the fast pointer is at the end is that, as our slow pointer is travelling with half the speed of fast pointer so when the fast pointer will reach the end of the linked list, till that time slow pointer will have only travelled half the distance as travelled by fast pointer and hence it will be at the middle of the linked list.

Do you know what the above-explained method is called?

• This method is called the tortoise and hare method or the slow and fast pointer method. The slow and fast pointer method has been explained in detail in the approach section and the dry run.

Let us have a glance at the approach.

Approach (Optimal) To Make C Function To Print The Middle Of A Linked List

Let us see what the slow and fast pointer technique is:

• Initially, both the pointers will point to the head of the linked list.

• Then, we will move both of the pointers.

  • The fast pointer will jump two places, whereas the slow pointer will one place.

• When the fast pointer will reach the end of the linked list, the slow pointer will be pointing to the middle of the linked list.

Algorithm To Make C Function To Print The Middle Of A Linked List

• Create two pointers say slow and fast. Initially, point both the slow and the fast to the head of the list.
• Now, the slow will jump one place, and the fast will jump two places until the fast reaches the end of the list.
• When the fast pointer reaches the end of the list, the slow will be pointing to the middle of the list.
• In the end, return the data of the slow pointer, as the slow will be pointing to the middle of the list.

Dry Run To Make C Function To Print The Middle Of A Linked List

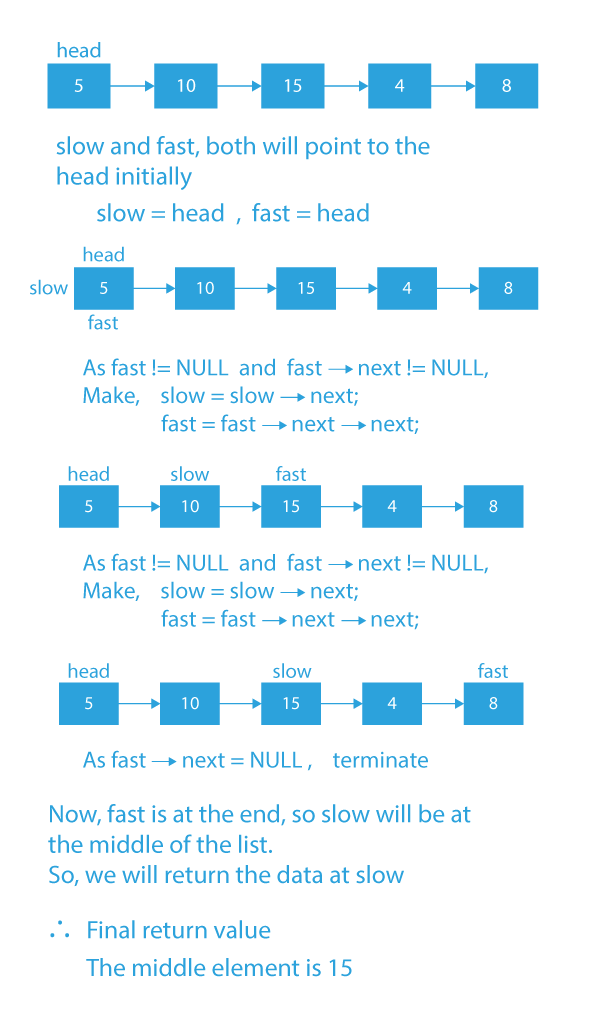
Code Implementation To Make C Function To Print The Middle Of A Linked List

#include<stdio.h>
#include<stdlib.h>

// Node structure of a linked list node
struct Node
{
    int data;
    struct Node* next;
};

// Using this function we will find and print the middle of the linked list
void findMiddle(struct Node *head)
{
    struct Node *slow_ptr = head;
    struct Node *fast_ptr = head;

    if (head!=NULL)
    {
        while (fast_ptr != NULL && fast_ptr->next != NULL)
        {
            fast_ptr = fast_ptr->next->next;
            slow_ptr = slow_ptr->next;
        }
        printf("The middle element is %d\n\n", slow_ptr->data);
    }
}

// Using this function we will create a new node and will insert at the beginning of the list
void push(struct Node** head_ref, int new_data)
{
    struct Node* new_node =
        (struct Node*) malloc(sizeof(struct Node));

    new_node->data = new_data;

    new_node->next = (*head_ref);

    (*head_ref) = new_node;
}

// Using this function we will print the linked list
void printList(struct Node *ptr)
{
    while (ptr != NULL)
    {
        printf("%d->", ptr->data);
        ptr = ptr->next;
    }
    printf("NULL\n");
}

// Driver Function
int main()
{
    struct Node* head = NULL;
    int i;
    push(&head,8);
    push(&head,4);
    push(&head,15);
    push(&head,10);
    push(&head,5);
    printf("The Linked List is : ");
    printList(head);
    findMiddle(head);
    return 0;
}

Output:
The Linked List is : 5->10->15->4->8->NULL
The middle element is 15

Time Complexity To Make C Function To Print The Middle Of A Linked List: O(n), a single list traversal is needed.

This blog had discussed both the optimized as well as naive approach to make C function to print the middle of a linked list. This is an important concept when it comes to coding interviews. The efficiency of this implementation is what makes this question an important one for coding interviews. If you want to solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.

FAQ

1. Can we add an element in the middle of Linkedlist?
You can add elements to either the beginning, middle or end of the linked list.

2. What is the time complexity to print the middle element in the linked list?
The running time of finding the middle element this way with two pointers is O(n) because once we pass through the entire linked list of n elements, the slower pointer is at the middle node already.

3. How will you find the middle of a Linkedlist in a single iteration?
In each iteration, the ptr1 will access the two nodes and the ptr2 will access the single node of the linked list. Now, when the ptr1 reaches the end of the linked list, the ptr2 will be in the middle. In this way, we are able to get the middle of the linked list in a single iteration.