Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Queues

Applications of Queue in Data Structure

Ankit Kochar

Last Updated on April 13, 2023 by Prepbytes

Queues are essential in the data structure, used to manage collections of elements that need to be processed in a particular order. They have multiple applications in operating systems, network protocols and other application of queue in data structure.

What is Queue in Data Structures?

A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle, meaning that the first element added to the queue will be the first one removed. Queues are commonly used in computer science for managing and organizing data in a specific order.

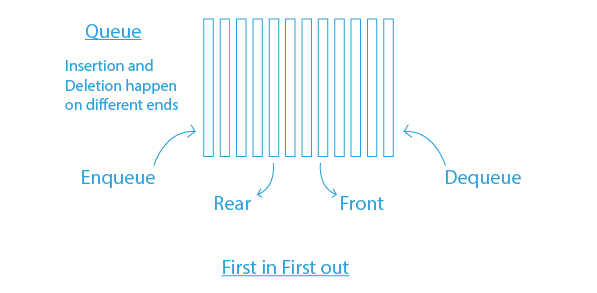
Basic Operations of Queue in Data Structure

  • Enqueue: This function is used to add an element to the rear end of the queue. If the queue is filled, then it will be in an overflow condition. The time complexity of the enqueue is O(1).
  • Dequeue: This function is used to remove an element from the front end of the queue. If the queue is empty, then it will be in an underflow condition. The time complexity of the dequeue is O(1).
  • Front: This function returns the front element of the queue. The time complexity of this function is O(1).
  • Rear: This function returns the last element of the queue. The time complexity of this function is O(1).
  • Peek(): This operation is used to get the value of the element from the front of the queue.

Types of Queues in Data Structures

There are four types of queues in data structures:

  • Simple Queue: In a Simple queue, insertion of the element takes place at the rear end i.e. ENQUEUE and removal of the element takes place at the front end i.e. DEQUEUE. The simple queue is also called a linear queue.
  • Circular Queue: In a circular queue, the elements act like circular rings. The working of a circular queue is similar to a simple queue but in a circular queue, the element in the last position is connected to the element in the first position. The main advantage of a circular queue is that the memory will be utilized in a better way.
  • Priority Queue: In a priority queue, the elements are stored according to their priority, Based on the priority of elements we’ll set our queue accordingly i.e. in ascending order or in descending order.
  • Dequeue: Dequeue is known as a double-ended queue. In dequeue, the elements can be inserted or removed from both ends.Due to this property, the dequeue may not follow the first in first out property

Implementation of Queue using Arrays

For the implementation of queue using arrays, we need to initialize two pointers i.e. front and rear, we insert an element from the rear and remove the element from the front, and if we increment the rear and front pointers we may occur error, Due to this, the front pointer may reach the end.
The solution to the above problem is to increase the front and rear pointers circularly.

Enqueue Operation / Insertion:

  • First, check if the queue is full or not.
  • For the first element, set the FRONT pointer to 0.
  • Increment the REAR index by 1.
  • Add the new element in the position which was pointed by REAR.

Dequeue Operation / Remove:

  • First, check if the queue is empty or not.
  • Return the value which was pointed by FRONT.
  • Increment the FRONT index by 1.
  • For the last element, reset the values of FRONT and REAR to -1.
#include 
#include 
#include 
 
struct Queue {
	int front, rear, size;
	unsigned capacity;
	int* array;
};
struct Queue* createQueue(unsigned capacity)
{
	struct Queue* queue = (struct Queue*)malloc(
		sizeof(struct Queue));
	queue->capacity = capacity;
	queue->front = queue->size = 0;
 
 
	queue->rear = capacity - 1;
	queue->array = (int*)malloc(
		queue->capacity * sizeof(int));
	return queue;
}
 
int isFull(struct Queue* queue)
{
	return (queue->size == queue->capacity);
}
 
int isEmpty(struct Queue* queue)
{
	return (queue->size == 0);
}
 
void enqueue(struct Queue* queue, int item)
{
	if (isFull(queue))
		return;
	queue->rear = (queue->rear + 1)
				% queue->capacity;
	queue->array[queue->rear] = item;
	queue->size = queue->size + 1;
	printf("%d enqueued to queue\n", item);
}
 
int dequeue(struct Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	int item = queue->array[queue->front];
	queue->front = (queue->front + 1)
				% queue->capacity;
	queue->size = queue->size - 1;
	return item;
}
 
int front(struct Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	return queue->array[queue->front];
}
 
int rear(struct Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	return queue->array[queue->rear];
}
 
int main()
{
	struct Queue* queue = createQueue(1000);
 
	enqueue(queue, 1);
	enqueue(queue, 2);
	enqueue(queue, 3);
	enqueue(queue, 4);
 
	printf("%d dequeued from queue\n\n",
		dequeue(queue));
 
	printf("Front item is %d\n", front(queue));
	printf("Rear item is %d\n", rear(queue));
 
	return 0;
}



#include <bits/stdc++.h>
using namespace std;


class Queue {
public:
	int front, rear, size;
	unsigned capacity;
	int* array;
};

Queue* createQueue(unsigned capacity)
{
	Queue* queue = new Queue();
	queue->capacity = capacity;
	queue->front = queue->size = 0;

	queue->rear = capacity - 1;
	queue->array = new int[queue->capacity];
	return queue;
}

int isFull(Queue* queue)
{
	return (queue->size == queue->capacity);
}

int isEmpty(Queue* queue)
{
	return (queue->size == 0);
}

void enqueue(Queue* queue, int item)
{
	if (isFull(queue))
		return;
	queue->rear = (queue->rear + 1)
				% queue->capacity;
	queue->array[queue->rear] = item;
	queue->size = queue->size + 1;
	cout << item << " enqueued to queue\n";
}

int dequeue(Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	int item = queue->array[queue->front];
	queue->front = (queue->front + 1)
				% queue->capacity;
	queue->size = queue->size - 1;
	return item;
}

int front(Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	return queue->array[queue->front];
}

int rear(Queue* queue)
{
	if (isEmpty(queue))
		return INT_MIN;
	return queue->array[queue->rear];
}

int main()
{
	Queue* queue = createQueue(1000);

	enqueue(queue, 1);
	enqueue(queue, 2);
	enqueue(queue, 3);
	enqueue(queue, 4);

	cout << dequeue(queue)
		<< " dequeued from queue\n";

	cout << "Front item is "
		<< front(queue) << endl;
	cout << "Rear item is "
		<< rear(queue) << endl;

	return 0;
}



class Queue {
	int front, rear, size;
	int capacity;
	int array[];

	public Queue(int capacity)
	{
		this.capacity = capacity;
		front = this.size = 0;
		rear = capacity - 1;
		array = new int[this.capacity];
	}

	boolean isFull(Queue queue)
	{
		return (queue.size == queue.capacity);
	}

	boolean isEmpty(Queue queue)
	{
		return (queue.size == 0);
	}

	void enqueue(int item)
	{
		if (isFull(this))
			return;
		this.rear = (this.rear + 1)
					% this.capacity;
		this.array[this.rear] = item;
		this.size = this.size + 1;
		System.out.println(item
						+ " enqueued to queue");
	}


	int dequeue()
	{
		if (isEmpty(this))
			return Integer.MIN_VALUE;

		int item = this.array[this.front];
		this.front = (this.front + 1)
					% this.capacity;
		this.size = this.size - 1;
		return item;
	}

	int front()
	{
		if (isEmpty(this))
			return Integer.MIN_VALUE;

		return this.array[this.front];
	}

	int rear()
	{
		if (isEmpty(this))
			return Integer.MIN_VALUE;

		return this.array[this.rear];
	}
}

class Test {
	public static void main(String[] args)
	{
		Queue queue = new Queue(1000);

		queue.enqueue(1);
		queue.enqueue(2);
		queue.enqueue(3);
		queue.enqueue(4);

		System.out.println(queue.dequeue()
						+ " dequeued from queue\n");

		System.out.println("Front item is "
						+ queue.front());

		System.out.println("Rear item is "
						+ queue.rear());
	}
}


class Queue:

	# __init__ function
	def __init__(self, capacity):
		self.front = self.size = 0
		self.rear = capacity -1
		self.Q = [None]*capacity
		self.capacity = capacity

	def isFull(self):
		return self.size == self.capacity
	

	def isEmpty(self):
		return self.size == 0

	def EnQueue(self, item):
		if self.isFull():
			print("Full")
			return
		self.rear = (self.rear + 1) % (self.capacity)
		self.Q[self.rear] = item
		self.size = self.size + 1
		print("% s enqueued to queue" % str(item))


	def DeQueue(self):
		if self.isEmpty():
			print("Empty")
			return
		
		print("% s dequeued from queue" % str(self.Q[self.front]))
		self.front = (self.front + 1) % (self.capacity)
		self.size = self.size -1
		
	def que_front(self):
		if self.isEmpty():
			print("Queue is empty")

		print("Front item is", self.Q[self.front])
		
	def que_rear(self):
		if self.isEmpty():
			print("Queue is empty")
		print("Rear item is", self.Q[self.rear])


if __name__ == '__main__':

	queue = Queue(30)
	queue.EnQueue(1)
	queue.EnQueue(2)
	queue.EnQueue(3)
	queue.EnQueue(4)
	queue.DeQueue()
	queue.que_front()
	queue.que_rear()

Time Complexity:

  • Enqueue: O(1)
  • Dequeue: O(1)
  • Front: O(1)
  • Rear: O(1)

Space Complexity:
O(N) where N is the size of the array.

Some of the Application of Queue in Data Structure

Here are some of the common application of queue in data structure:

  • Queues can be used to schedule jobs and ensure that they are executed in the correct order.
  • Queues can be used to manage the order in which print jobs are sent to the printer.
  • Queues are used to implement the breadth-first search algorithm.
  • Queues can be used to manage incoming calls and ensure that they are handled in the correct order.
  • Queues can be used to manage the order in which processes are executed on the CPU.
  • Queues can be used for buffering data while it is being transferred between two systems. When data is received, it is added to the back of the queue, and when data is sent, it is removed from the front of the queue.

Other Application of Queue in Data Structure

Some other application of queue in data structure:

  • Applied as buffers on playing music in the mp3 players or CD players.
  • Applied on handling the interruption in the operating system.
  • Applied to add a song at the end of the playlist.
  • Applied as the waiting queue for using the single shared resources like CPU, Printers, or Disk.
  • Applied to the chat application when someone sends messages to us and we don’t have an internet connection then the messages are stored in the server of the chat application

Application of Queue in Networks

Some of the applications of the queue in networks:

  • The switches and routers play an important part in networks and we can use queues with them.
  • There are various mail queues in networks.
  • In networks, we can use a variety of queues like Priority Queue, Deque, etc.

Application of Queue in Operating System

Some of the applications of the queue in OS:

  • They can be used for algorithms like First Come First Serve(FCFS).
  • It is used as a buffer for input devices like the Keyboard.
  • It is also used for CPU Scheduling.
  • It is widely used for spooling in Printers.
  • Queues are also used in Memory Management.

Conclusion
In conclusion, application of queue in data structure are widely used in computer science to manage and organize data in a specific order. They follow the FIFO principle and can be implemented using arrays or linked lists. Queues have numerous applications, including job scheduling, printer spooling, breadth-first search, call centre management, CPU task management, and buffering. Queues are essential tools for efficiently managing and organizing data in a way that ensures tasks are executed in the correct order.

Frequently Asked questions(FAQs)

Q1. What is the queue Data structure?
Ans: queue is defined as the ordered list in which insertion and deletion are performed at two different ends i.e. REAR and FRONT end.

Q2. What are the types of queue data structures?
Ans: There are four types of queue data structures:

  • Simple queue
  • Circular queue
  • Priority queue
  • Dequeue

Q3. What are the REAR and FRONT end?
Ans: Queue is a collection of elements that are added at one end called “REAR” and removed from the other end called “FRONT”.

Q4. How do queues optimize the management of data?
Ans: Queues optimize the management of data by ensuring that tasks or data are executed or processed in the correct order. By following the FIFO principle, queues make it easy to organize and manage data based on the order in which it was received.

Q5. What are the applications of a queue in data structures?
Ans: Queues have various applications in computer science and information technology. Some of the commonly used applications are:

  • CPU scheduling in operating systems
  • Network packet scheduling
  • Printer job scheduling
  • Breadth-First Search (BFS) algorithm
  • Simulation modeling
  • Traffic management in communication networks
  • Call center management
  • Web server request handling
  • Bank teller management
  • Producer-consumer problem

Also, You can checkout given below Queue Articles for better understanding:
1. Advantages of circular queue
2. Difference between linear queue and circular queue
3. Reverse a queue

Leave a Reply

Your email address will not be published. Required fields are marked *

Close

Related Post