Last Updated on December 13, 2022 by Prepbytes

Introduction
The linked list is one of the most important concepts and data structures to learn while preparing for interviews. Having a good grasp of Linked Lists can be a huge plus point in a coding interview.
Problem Statement
Here in this problem we will be implementing a priority queue using a linked list.
Problem Statement Understanding
There are 3 main operations in a priority queue:
- push() – to insert a new element into the queue.
- pop() – to remove the highest priority element from the queue.
- peep() – to retrieve the highest priority element, without removing it from the queue.
What we are going to do is, create a linked list, but with a few tweaks, the list will be created in such a way, that the highest priority element will always be the head of the linked list. That means the list will be sorted in the descending order of the elements based on their priority. By doing this, we can do the peek() operation in O(1) time.
For the push() operation, we have to find a suitable position to insert the current node so that the overall order of the priority queue is maintained. This will take O(n) time. Let us have a look at the approaches.
Approach(push)
In the push function, we have to first find the suitable position for the value to be inserted. We have to traverse through the list and find the node which has a lower priority than the current node. This is going to maintain the decreasing order of the priority queue.
Algorithm
- Create a new node.
- If the priority of the current node is greater than the head’s priority, then insert at the beginning and make the current node the head of the list.
- Else, find the appropriate position to insert the current node according to the descending order of their priorities. We can do this by traversing through the list.
- After the appropriate node is found i.e. the node whose priority is lesser than the new node’s priority, store it in X, just for the sake of simplicity.
- Now, insert the new node just before X, as the new node’s priority is greater than X.
Approach(pop)
In the pop function, we will increment the head as head -> next. This will delete the head.
Algorithm
- Create a new node temp and its value will be the head.
- Now, increment the head as head = head – > next. This will delete the current node.
- Now, there is a memory leak. A memory leak happens when we remove the links of a node, but do not free it from the memory. Although the node is remove from the linked list, it still says in the memory.
- To remove the memory leak, we can use the free method free(temp)
- The free method remove the passed node from the memory.
Approach(peek)
The work of the peek function is to retrieve the highest priority element, without removing it from the queue.
So, we will simply return the head -> data , as the head will always contain the highest priority element.
Algorithm
- Return head – > data, as the head will always contain the highest priority element.
Dry Run
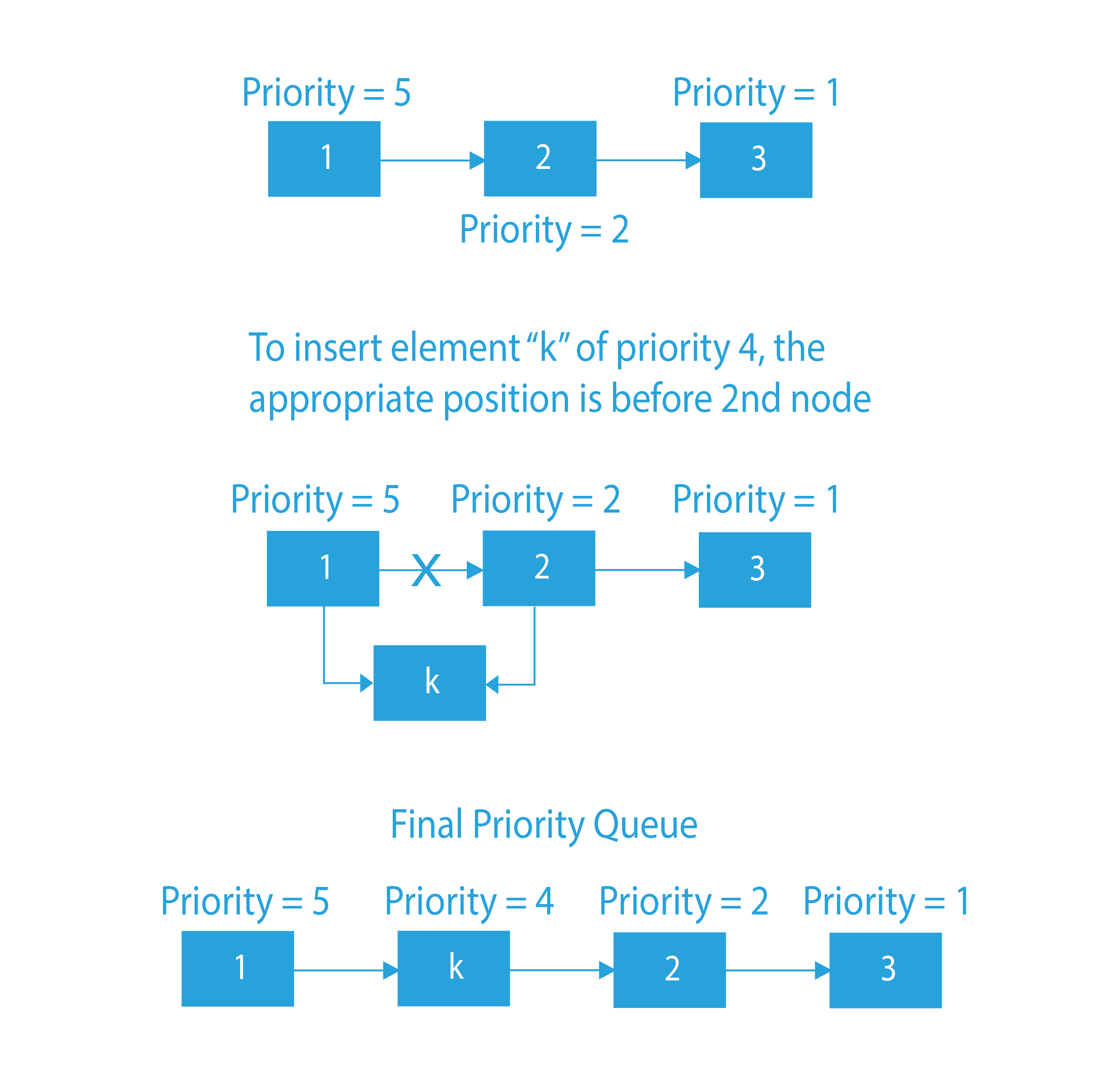
Code Implementation
#include#include // priority Node typedef struct node { int data; int priority; struct node* next; } Node; Node* newNode(int d, int p) { Node* temp = (Node*)malloc(sizeof(Node)); temp->data = d; temp->priority = p; temp->next = NULL; return temp; } int peek(Node** head) { return (*head)->data; } void pop(Node** head) { Node* temp = *head; (*head) = (*head)->next; free(temp); } void push(Node** head, int d, int p) { Node* start = (*head); Node* temp = newNode(d, p); if ((*head)->priority > p) { temp->next = *head; (*head) = temp; } else { while (start->next != NULL && start->next->priority < p) { start = start->next; } // Either at the ends of the list // or at required position temp->next = start->next; start->next = temp; } } // Function to check the queue is empty int isEmpty(Node** head) { return (*head) == NULL; } // main function int main() { Node* pq = newNode(7, 1); push(&pq, 1, 2); push(&pq, 3, 3); push(&pq, 2, 0); while (!isEmpty(&pq)) { printf("%d ", peek(&pq)); pop(&pq); } return 0; }
#includeusing namespace std; typedef struct node { int data; int priority; struct node* next; } Node; Node* newNode(int d, int p) { Node* temp = (Node*)malloc(sizeof(Node)); temp->data = d; temp->priority = p; temp->next = NULL; return temp; } int peek(Node** head) { return (*head)->data; } void pop(Node** head) { Node* temp = *head; (*head) = (*head)->next; free(temp); } void push(Node** head, int d, int p) { Node* start = (*head); Node* temp = newNode(d, p); if ((*head)->priority > p) { temp->next = *head; (*head) = temp; } else { while (start->next != NULL && start->next->priority < p) { start = start->next; } temp->next = start->next; start->next = temp; } } int isEmpty(Node** head) { return (*head) == NULL; } int main() { Node* pq = newNode(3, 1); push(&pq, 2, 2); push(&pq, 1, 5); push(&pq, 4, 4); while (!isEmpty(&pq)) { cout << " " << peek(&pq); pop(&pq); } return 0; }
import java.util.* ;
public class Solution
{
static class Node {
int data;
int priority;
Node next;
}
static Node node = new Node();
static Node newNode(int d, int p)
{
Node temp = new Node();
temp.data = d;
temp.priority = p;
temp.next = null;
return temp;
}
static int peek(Node head)
{
return (head).data;
}
static Node pop(Node head)
{
Node temp = head;
(head) = (head).next;
return head;
}
static Node push(Node head, int d, int p)
{
Node start = (head);
Node temp = newNode(d, p);
if ((head).priority > p) {
temp.next = head;
(head) = temp;
}
else {
while (start.next != null &&
start.next.priority < p) {
start = start.next;
}
temp.next = start.next;
start.next = temp;
}
return head;
}
static int isEmpty(Node head)
{
return ((head) == null)?1:0;
}
public static void main(String args[])
{
Node pq = newNode(3, 1);
pq =push(pq, 2, 2);
pq =push(pq, 1, 5);
pq =push(pq, 4, 4);
while (isEmpty(pq)==0) {
System.out.printf("%d ", peek(pq));
pq=pop(pq);
}
}
}
class PriorityQueueNode:
def __init__(self, value, pr):
self.data = value
self.priority = pr
self.next = None
class PriorityQueue:
def __init__(self):
self.front = None
def isEmpty(self):
return True if self.front == None else False
def push(self, value, priority):
if self.isEmpty() == True:
self.front = PriorityQueueNode(value,
priority)
return 1
else:
if self.front.priority > priority:
newNode = PriorityQueueNode(value, priority)
newNode.next = self.front
self.front = newNode
return 1
else:
temp = self.front
while temp.next:
if priority <= temp.next.priority:
break
temp = temp.next
newNode = PriorityQueueNode(value,
priority)
newNode.next = temp.next
temp.next = newNode
return 1
def pop(self):
if self.isEmpty() == True:
return
else:
self.front = self.front.next
return 1
def peek(self):
if self.isEmpty() == True:
return
else:
return self.front.data
def traverse(self):
if self.isEmpty() == True:
return "Queue is Empty!"
else:
temp = self.front
while temp:
print(temp.data, end = " ")
temp = temp.next
if __name__ == "__main__":
pq = PriorityQueue()
pq.push(3, 1)
pq.push(2, 2)
pq.push(1, 5)
pq.push(4, 4)
pq.traverse()
pq.pop()
Output
3 2 4 1
Time Complexity
peek() – O(1)
push() – O(n), as list traversal is needed.
pop() – O(1)
[forminator_quiz id=”3637″]
So, in this article, we have tried to explain the most efficient approach to implement a priority queue using a linked list. This is a very interesting way to implement a priority queue, and that is what makes this problem an important one for coding interviews. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.


