Find the largest node in a Doubly Linked List

Last Updated on March 10, 2022 by Ria Pathak

Introduction

The linked list is one of the most important concepts and data structures to learn while preparing for interviews. Having a good grasp of Linked Lists can be a huge plus point in a coding interview.

Problem Statement

In this question, we are given a doubly linked list. We have to find the largest node in that list.

Problem Statement Understanding

We have to find the largest node in a doubly linked list. Let the Doubly Linked List be DLL = 1 2 3 4.

Now, in the given list, the largest value node is 4. Therefore, the output of our program will be 4.

Input:

Output: 4

Explanation: The largest value node is 4.

This question is not a very complex one. We have to make use of list traversal in the question. Let us have a look at the approach.

Approach

The approach is going to be pretty simple. We will create a new node MAX, and make it point to the head node. Then we will traverse the list and keep comparing the MAX’s data with every node’s data of the list. If at any point, the value of any node’s data is greater than MAX’s data, then we will make MAX point to that node.

In the end, the MAX will contain our answer.

Algorithm

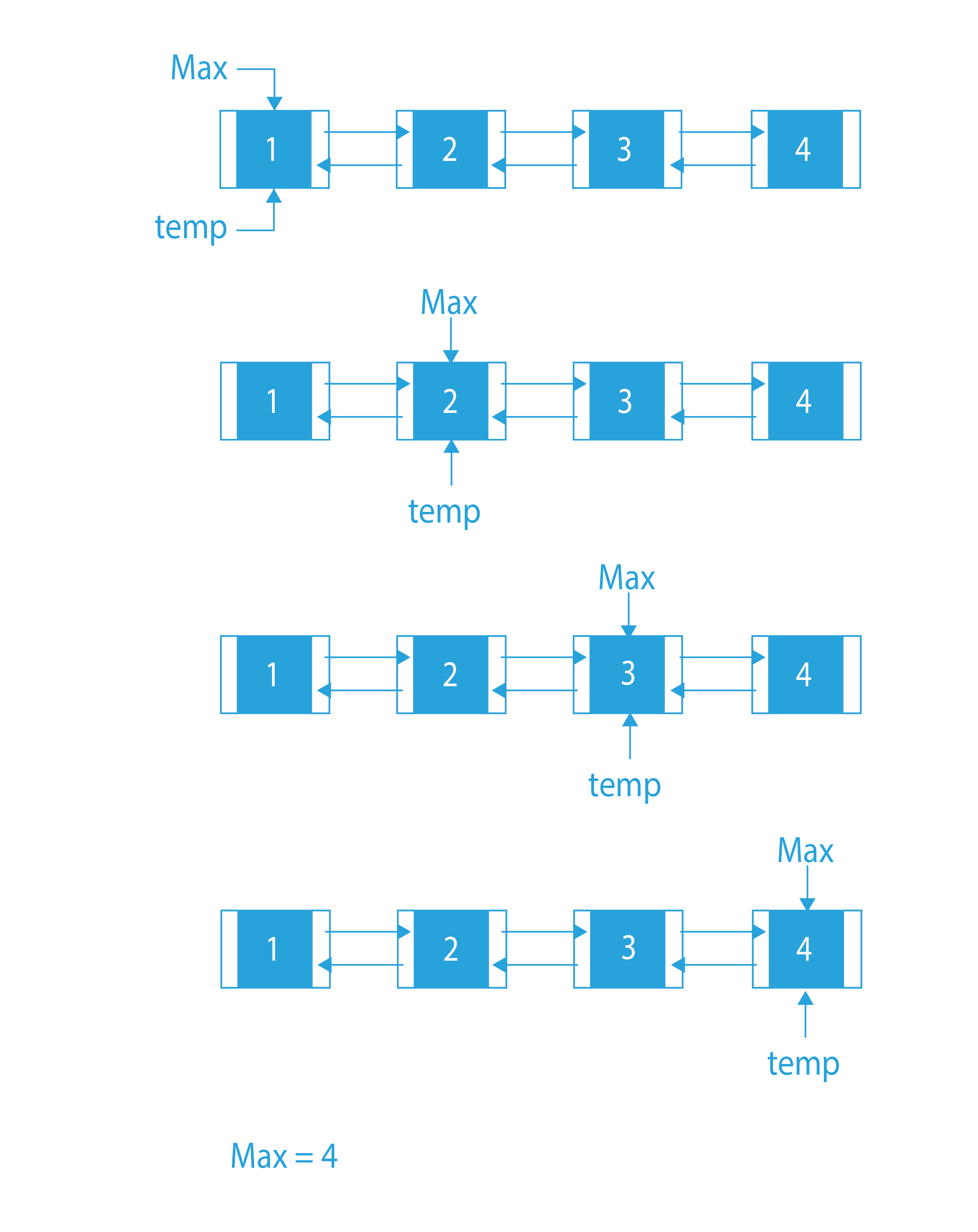
• Initialize the temp and the MAX to the head. Now, traverse through the whole list.
• If at any point, temp’s data is greater than MAX’s data, then we will put MAX=temp.
• Keep traversing until we reach the end. MAX is going to contain the node whose data has the maximum value.

Dry Run

Code Implementation

Find the largest node in a Doubly Linked List

#include 
using namespace std;

struct Node
{
    int data;
    struct Node* next;
    struct Node* prev;
};

void push(struct Node** head_ref, int new_data)
{
    struct Node* new_node =
    (struct Node*)malloc(sizeof(struct Node));

    new_node->data = new_data;

    new_node->prev = NULL;

    new_node->next = (*head_ref);

    if ((*head_ref) != NULL)
        (*head_ref)->prev = new_node;

    (*head_ref) = new_node;
}

int LargestInDLL(struct Node** head_ref)
{
    struct Node *max, *temp;

    temp = max = *head_ref;

    while (temp != NULL)
    {

        if (temp->data > max->data)
            max = temp;
 
        temp = temp->next;
    }
    return max->data;
}

int main()
{
    struct Node* head = NULL;
    push(&head, 4);
    push(&head, 3);
    push(&head, 2);
    push(&head, 1);
 
    cout << LargestInDLL(&head);
    return 0;
}

public class PrepBytes {

    static class Node {
        int data;
        Node next;
        Node prev;
    };


    static Node push(Node head_ref, int new_data)
    {

        Node new_node = new Node();


        new_node.data = new_data;

        new_node.prev = null;


        new_node.next = (head_ref);


        if ((head_ref) != null)
            (head_ref).prev = new_node;


        (head_ref) = new_node;
        return head_ref;
    }

    static int LargestInDLL(Node head_ref)
    {
        Node max, temp;

        temp = max = head_ref;

        while (temp != null) {

            if (temp.data > max.data)
                max = temp;

            temp = temp.next;
        }
        return max.data;
    }

    public static void main(String args[])
    {
        Node head = null;
        head = push(head, 4);
        head = push(head, 3);
        head = push(head, 2);
        head = push(head, 1);

        System.out.printf("%d", LargestInDLL(head));
    }
}

Output
4

Time Complexity: O(n), since we are traversing the linked list once.
Space Complexity: O(1), as only temporary variables are being created.

So, in this article, we have tried to explain the most efficient approach to find the largest node in a doubly-linked list. This is a simple question that tests our basic concepts of doubly-linked lists. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.