Last Updated on June 17, 2022 by Ria Pathak

Concepts Used
Sorting
Difficulty Level
Medium
Problem Statement (Simplified):
Find the minimum length of the subarray when sorted completely sorts the given array.
See original problem statement here
Test Case
Input:
2
8
1 3 2 7 5 6 4 8
10
1 2 5 3 4 6 8 7 10 9
Output:
1 6
2 9
Explanation:
Case-1:
In the given array, subarray starting from index 0 to 6 is unsorted, so if we sort this window, we get the whole array sorted. The sorted array will be 1 [2 3 4 5 6 7] 8.
Case-2:
In the given array, subarray starting from index 2 to 9 is unsorted, so if we sort this window, we get the whole array sorted. Sorted array will be 1 2 [3 4 5 6 7 8 9 10].Solving Approach :
Observation:
We can see that size of array goes from 1 to 106, in worse conditions let the size of the array be 106 if we sort this array using any of sorting techniques i.e. Bubble Sort, Insertion Sort, Selection sort. They all take O(N2) in worst cases, which results in 1012 iterations when the size of the array is 106. So we, can’t choose the above three sorting algorithms. We use Merge Sort to sort array as it sorts array in linearithmic time complexity (nlog(n)).
1) As we know, there’s only a single smaller portion of the array which is not sorted.
2) If we sort the array, and check how many elements of the array are sorted from both ends we can solve this problem.
3) The elements which disobey the non-decreasing behavior of array at both ends are our start and endpoint of an unsorted array.
Example
Let array
Abe,
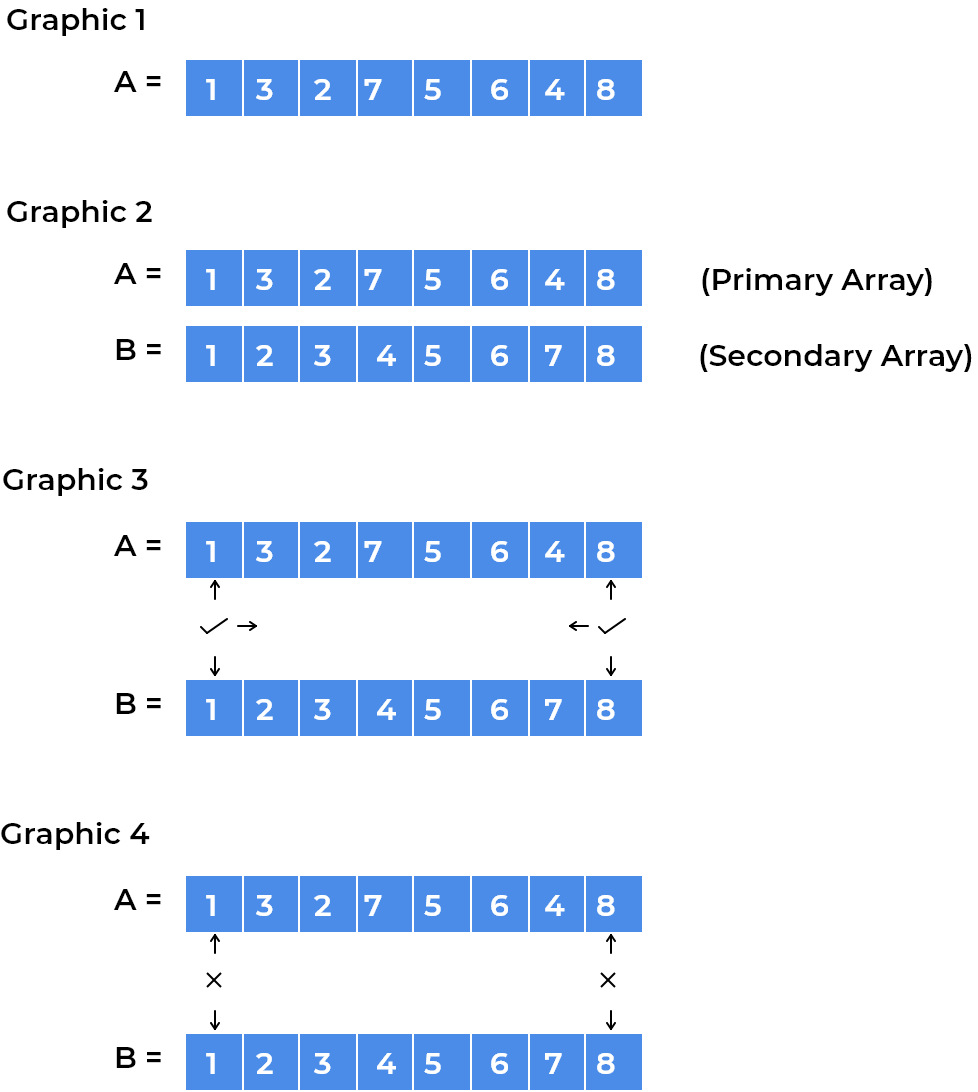
We copy array
Ain a secondary arrayBfor later comparisions, we also sort arrayBto match elements,After sorting array
B, we have both arrays like this,We, then iterate from both ends, and check index at which element differs in both arrays, Once we get that, we set the index to
startindex orendindex denoting index of unsorted window, if elements are equal, we proceed further until bothstartandendhas a valid index, if during iteration we cross the middle index, that means there exists no window which is not sorted.Iterations are as follows :
Iteration – 1
After iteration,
startandendboth remains-1,so we move to next iteration.
Iteration – 2
After iteration, We can see elements at index are not same in both arrays
AandB, so we save the index tostart, same can be observed at other end, so we also save index from another end inendvariable. As both pointersstartandendhave some values in them, so we come out of loop. And unsorted sub-array starts fromstartindex and ends atendindex
Solutions
#include <stdio.h>
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1];
int right[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
scanf("%d",&test);
while(test--){
int n;
scanf("%d",&n);
int arr[n], sorted[n];
for(int i=0; i<n; i++){
scanf("%d",&arr[i]);
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int start = -1, end = -1;
for(int i=0; i<n/2; i++){
if(start!=-1 && end!=-1)
break;
if(start == -1 && arr[i]!=sorted[i])
start = i;
if(end == -1 && arr[n-i-1]!=sorted[n-i-1])
end = n-i-1;
}
printf("%d %d\n",start,end);
}
}
#include <bits/stdc++.h>
using namespace std;
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1]={0};
int right[end-mid]={0};
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
cin>>test;
while(test--){
int n;
cin>>n;
int arr[n], sorted[n];
for(int i=0; i<n; i++){
cin>>arr[i];
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int start = -1, end = -1;
for(int i=0; i<n/2; i++){
if(start!=-1 && end!=-1)
break;
if(start == -1 && arr[i]!=sorted[i])
start = i;
if(end == -1 && arr[n-i-1]!=sorted[n-i-1])
end = n-i-1;
}
cout<<start<<" "<<end<<endl;
}
}
import java.util.*;
import java.io.*;
public class Main {
static void merge(int arr[], int start, int mid, int end){
int left[] = new int[mid-start+1];
int right[] = new int[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
static void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
public static void main(String args[]) throws IOException {
Scanner sc = new Scanner(System.in);
int test = sc.nextInt();
while(test--!=0){
int n = sc.nextInt();
int arr[] = new int[n], sorted[] = new int[n];
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int start = -1, end = -1;
for(int i=0; i<n/2; i++){
if(start!=-1 && end!=-1)
break;
if(start == -1 && arr[i]!=sorted[i])
start = i;
if(end == -1 && arr[n-i-1]!=sorted[n-i-1])
end = n-i-1;
}
System.out.println(start+" "+end);
}
}
}
def merge(arr, start, mid, end): left = [0 for i in range(mid - start + 1)] right = [0 for i in range(end - mid)] for i in range(start, mid + 1): left[i - start] = arr[i] for i in range(mid + 1, end + 1): right[i - (mid + 1)] = arr[i] leftIndex = 0 rightIndex = 0 arrIndex = start while leftIndex <= mid - start and rightIndex < end - mid: if(left[leftIndex] < right[rightIndex]): arr[arrIndex] = left[leftIndex] leftIndex += 1 else: arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 while(leftIndex <= mid - start): arr[arrIndex] = left[leftIndex] leftIndex += 1 arrIndex += 1 while(rightIndex < end - mid): arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 def mergeSort(arr, start, end): if(end == start): return mergeSort(arr, start, (start + end) // 2) mergeSort(arr, ((start + end) // 2) + 1, end) merge(arr, start, (start + end) // 2, end) for _ in range(int(input())): n = int(input()) arr = list(map(int, input().split())) sorted = arr.copy() mergeSort(sorted, 0, n - 1) start, end = -1, -1 for i in range(n // 2): if start != -1 and end != 1: break if start == -1 and arr[i] != sorted[i]: start = i if end == -1 and arr[n - i - 1] != sorted[n - i - 1]: end = n - i - 1 print(start, end)
Space Complexity
O(
n) for auxillary array to sort array.
[forminator_quiz id="1391"]
This article tried to discuss Sorting. Hope this blog helps you understand and solve the problem. To practice more problems on Sorting you can check out MYCODE | Competitive Programming.