Last Updated on June 17, 2022 by Ria Pathak

Concepts Used
Sorting
Difficulty Level
Medium
Problem Statement (Simplified):
We have to find a triplet
(n_{1}, n_{2}, n_{3})in array such that sum of two number i.e.n_{1}+n_{2}equals to the third numbern_{3}. We have to print the triplet inn_{3}n_{1}n_{2}formation.
See original problem statement here
Test Case
Input:
1
5
20 40 30 50 70
Output:
70 20 50
Explanation:
We can see there are two such triplets (70,20,50) and (50,20,30). As the first triplet has a higher sum value, so we print 70 20 50.Solving Approach :
Bruteforce Approach:
This problem can be solved if we form three loops for each number and check if the sum of two numbers is equal to the third number, we save all three numbers. Later all loops if no number is present in the array, we print -1. Else we print the largest of them. This approach takes O(n3 ) which is not efficient, so we can solve this more efficiently by given approach.
Efficient Approach :
1) We can find
n_{2}if we can subtractn_{1}fromn_{3}, so we need to find only the pairn_{3}andn_{1}.
2) We can maintain a hash table which saves the presence of numbers in the array, hash table returns 1 if the number is present in the array, else returns 0.
3) We also known_{3}will be a larger number in the array, so we can sort the array so that we can iterate all larger numbers serial wise from the last index of the array.
4) So we now iterate from the last index of the sorted array, and find any element from smaller side of the array such that difference of both numbers exists in the array if any such pair exists we print the larger number, smaller number and their difference.
Example
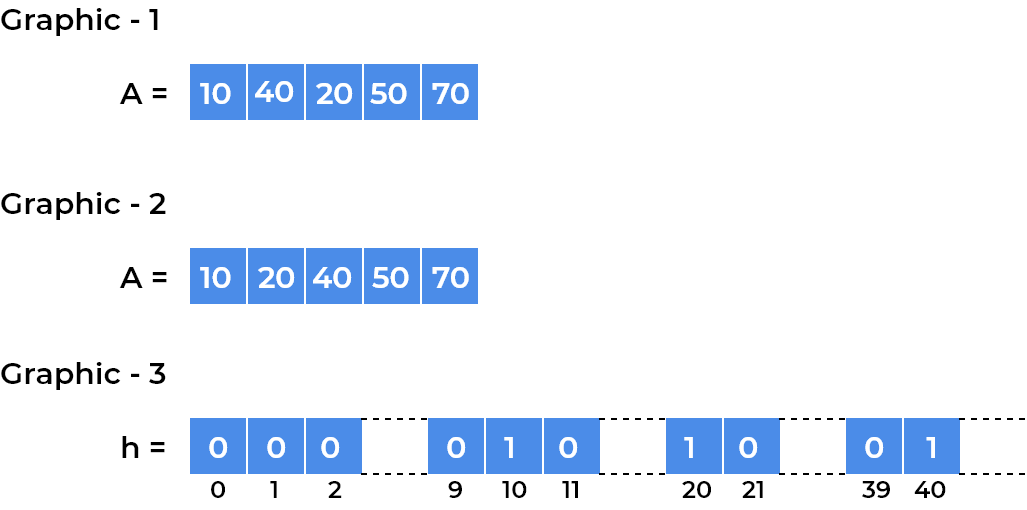
Let array
Abe,
Sorting array
Aand maintaining a hash tableHwhich stores value 1 if indexxis present in arrayA, else it stores 0.Sorted Array
A,Hash Table
H,Required equation is :
n_{1}+n_{2}=n_{3}For n_{3}, we iterate from last index of array
MARKDOWN_HASH7fc56270e7a70fa81a5935b72eacbe29MARKDOWNHASHas we need to print the largest value of n{3}, Let the iterator bej=4(last index)For n_{1}, we ierate from start of array
A, Let the iterator bei=0,
For
i=0, j=4:
A[i]= 10,A[j]= 70,
We check ifA[j] - A[i]is present in array or not, which can be verified from hash tableH,
h[A[j] - A[i]]
h[70 - 10]
h[60]
Ash[60]is 0, hence, this is not the required triplet, so we check next value of i i.e.i = 1,For
i=1, j=4:
A[i]= 20,A[j]= 70,
We check ifA[j] - A[i]is present in array or not, which can be verified from hash tableH,
h[A[j] – A[i]]`
h[70 - 20]
h[50]
Ash[50]is 1, hence, this is the required triplet, hence, we print the triplet in this form, i.e.A[i]A[j]-A[i]A[j]
Solutions
#include <stdio.h>
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1];
int right[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
scanf("%d",&test);
while(test--){
int n;
scanf("%d",&n);
int arr[n], hash[9999999]={0};
for(int i=0; i<n; i++){
scanf("%d",&arr[i]);
hash[arr[i]] = 1;
}
mergeSort(arr,0,n-1);
int flag = 1;
for(int i=n-1; i>=0; i--){
for(int j=0; j<n;j++){
if( arr[i]-arr[j]>=0 && hash[arr[i]-arr[j]]>0 && arr[i]-arr[j]!=arr[j]){
printf("%d %d %d\n",arr[i],arr[j], arr[i]-arr[j]);
flag = 0;
break;
}
}
if(!flag)
break;
}
if(flag)
printf("-1\n");
}
}
#include <bits/stdc++.h>
using namespace std;
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1]={0};
int right[end-mid]={0};
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
cin>>test;
while(test--){
int n;
cin>>n;
int arr[n], hash[9999999]={0};
for(int i=0; i<n; i++){
cin>>arr[i];
hash[arr[i]] = 1;
}
mergeSort(arr,0,n-1);
int flag = 1;
for(int i=n-1; i>=0; i--){
for(int j=0; j<n;j++){
if( arr[i]-arr[j]>=0 && hash[arr[i]-arr[j]]>0 && arr[i]-arr[j]!=arr[j]){
cout<<arr[i]<<" "<<arr[j]<<" "<<arr[i]-arr[j]<<endl;
flag = 0;
break;
}
}
if(!flag)
break;
}
if(flag)
cout<<-1<<endl;
}
}
import java.util.*;
import java.io.*;
public class Main {
static void merge(int arr[], int start, int mid, int end){
int left[] = new int[mid-start+1];
int right[] = new int[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
static void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
public static void main(String args[]) throws IOException {
Scanner sc = new Scanner(System.in);
int test = sc.nextInt();
while(test--!=0){
int n = sc.nextInt();
int arr[] = new int[n], hash[] = new int[9999999];
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
hash[arr[i]] = 1;
}
mergeSort(arr,0,n-1);
int flag = 1;
for(int i=n-1; i>=0; i--){
for(int j=0; j<n;j++){
if(arr[i]-arr[j]>=0 && hash[arr[i]-arr[j]]>0 && arr[i]-arr[j]!=arr[j]){
System.out.println(arr[i] + " " + arr[j] + " " + (arr[i]-arr[j]));
flag = 0;
break;
}
}
if(flag==0)
break;
}
if(flag==1)
System.out.println("-1");
}
}
}
def merge(arr, start, mid, end): left = [0 for i in range(mid - start + 1)] right = [0 for i in range(end - mid)] for i in range(start, mid + 1): left[i - start] = arr[i] for i in range(mid + 1, end + 1): right[i - (mid + 1)] = arr[i] leftIndex = 0 rightIndex = 0 arrIndex = start while leftIndex <= mid - start and rightIndex < end - mid: if(left[leftIndex] < right[rightIndex]): arr[arrIndex] = left[leftIndex] leftIndex += 1 else: arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 while(leftIndex <= mid - start): arr[arrIndex] = left[leftIndex] leftIndex += 1 arrIndex += 1 while(rightIndex < end - mid): arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 def mergeSort(arr, start, end): if(end == start): return mergeSort(arr, start, (start + end) // 2) mergeSort(arr, ((start + end) // 2) + 1, end) merge(arr, start, (start + end) // 2, end) for _ in range(int(input())): n = int(input()) hash = [0] * 9999999 arr = list(map(int, input().split())) for i in arr: hash[i] = 1 mergeSort(arr, 0, n - 1) flag = 1 for i in range(n - 1, -1, -1): for j in range(n): if arr[i] - arr[j] >= 0 and hash[arr[i] - arr[j]] > 0 and arr[i] - arr[j] != arr[j]: print(arr[i], arr[j], arr[i]- arr[j]) flag = 0 break if not flag: break if flag: print(-1) # your code goes here
[forminator_quiz id="1386"]
Space Complexity
O(
max(arrayelements) ) to maintain a hash table.
This article tried to discuss the concept of Sorting. Hope this blog helps you understand and solve the problem. To practice more problems on Sorting you can check out MYCODE | Competitive Programming.