Last Updated on July 27, 2023 by Mayank Dham

Introduction
This article aims to explore an efficient method of performing binary search on linked list. Binary search is a searching algorithm specifically designed for sorted data, where the target element is sought in the middle portion of the linked list. As we are aware, binary search is applicable only to sorted data.So let’s understand how can we perform a binary search on linked list.
How to Implement Binary Search on Linked List
In this problem, we are given a sorted Singly Linked List and an integer X, and we need to find and tell if the list contains a given element X or not.
Problem Statement Understanding
Let’s learn programming languages online and try to understand the problem statement with the help of examples.
If the given linked list is

- According to the problem statement, the given linked list is sorted, and we need to tell if the list contains element X or not.
- If element X is present we will print Element Found else we print Element not Found.
- We can see that X = 5 is present in the linked list, so we will print ‘Element Found’.
If the given sorted linked list is head→1→3→5→7→9→NULL and X=8.
- So we can see that X = 8 is not present in the given linked list, so we will print Element not Found.
Now I think from the above examples, the problem is clear. So let’s see how we can approach it.
A straightforward way to check if an element X is present in the linked list is to traverse the linked list and check if for any node (node→data == X):
- If node→data == X, it will mean that element X is present in the linked list.
- Otherwise, if none of the node’s data is equal to X during the whole traversal, it will mean that element X is not present in the linked list.
Although the above linear traversal to check if any element X is present in the linked list or not will work fine, but here we are asked to use Binary search.
So let’s see how we can use binary search to check if an element X is present in a linked list or not.
Approach of binary search on linked list
Here we will see how we can use binary search algorithm to check whether a certain element X is present in the given list or not.
Initially, the range of binary search will be the complete list, i.e., from head to the last node of the list. Binary search first compares the target element X with the middle element based on which it reduces the range for further search.
- If the middle element is equal to the target element X, then we have found our element.
- Else, if the target element X is less than the middle element, then the range of binary search will reduce, and our new range will be from start to middle element of the linked list.
- Else, If the target element X is greater than the middle element, the search range will reduce and our new search range will be from middle→next to the end of the list.
The searching will go on until one of the following condition hits:
- We find element X.
- The search range collapses, and we don’t have any element in the search range to check.
The time complexity of binary search on linked list is O(log n) which is much better than linear search which takes linear time O(n) to search an element, but for binary to work properly the given must be sorted. Its time complexity is less than O(n) because it does not check every element of the given list. The search reduces to half at every iteration.
Let’s see the algorithm.
Algorithm to perform binary search in linked list
To find an element X in the singly linked list, we need to find the middle of the list and then divide the list into 2 halves and perform the operations on the favorable part of the list and repeat the above steps until we find the required key in the list.
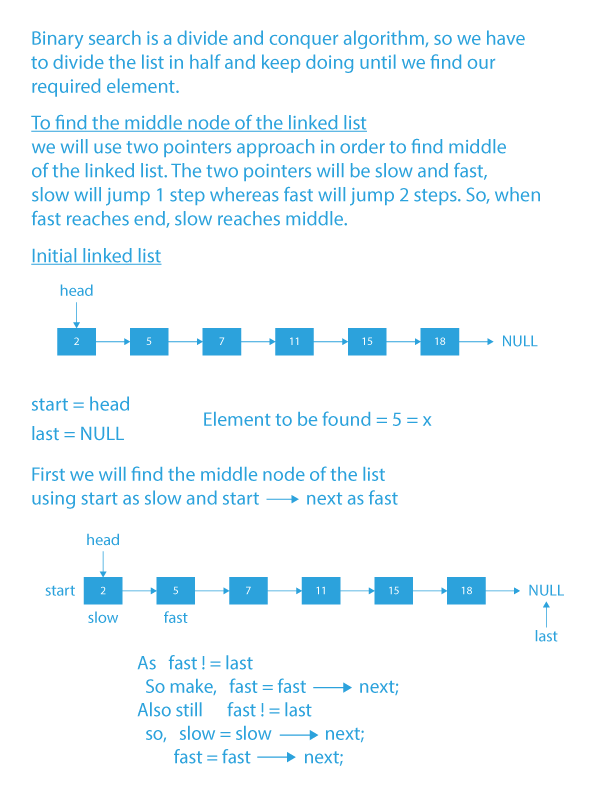
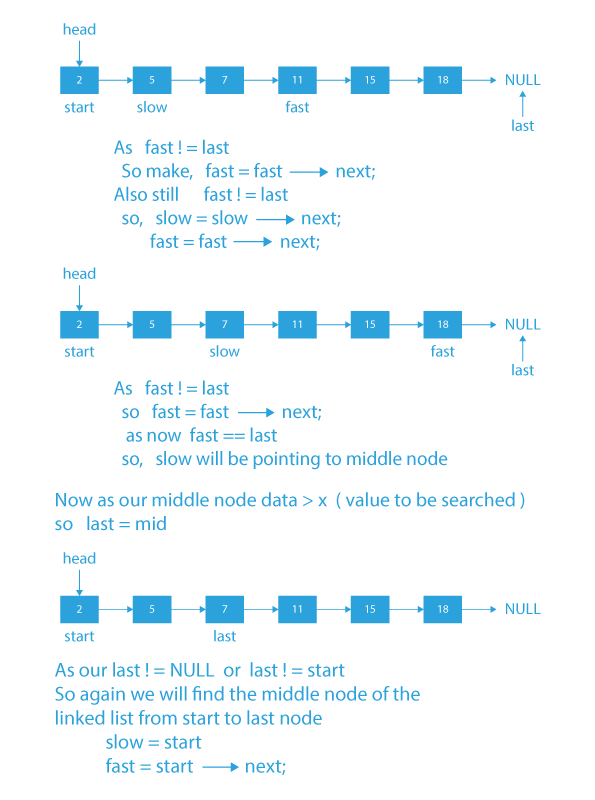
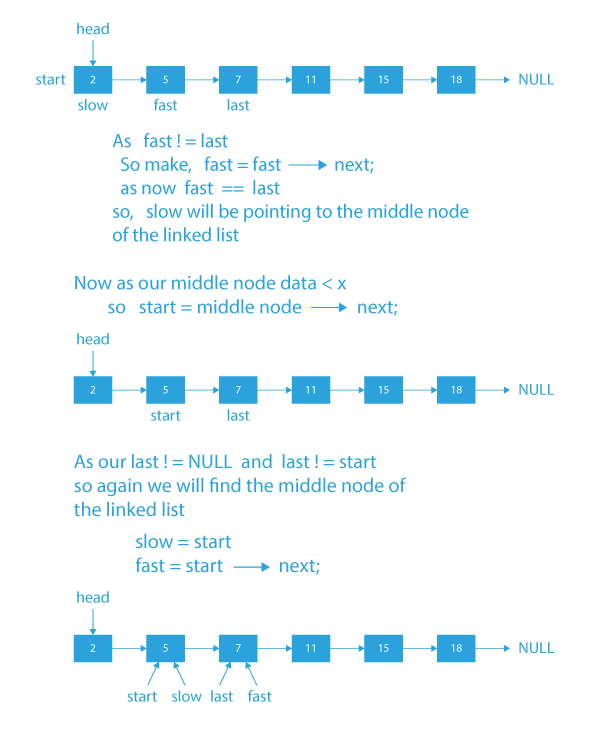
- First, we need to find the middle node of the linked list, which we will find using the slow and fast pointer method.
- In slow and fast pointer method, we will run a while loop until the fast pointer or next of the fast pointer hits null and in each iteration, we will move fast by 2 nodes at a time (fast = fast→next→next) and slow one node at a time ( slow=slow→next).
- So when the pointers exit the while loop, the slow pointer will be pointing to the middle node of the linked list.
- Then, after finding the middle node of the list, we need to compare the value of the middle node of the list with the target element X.
- If the middle node value of the list is equal to target element X, so we return middle as the answer.
- If the middle node value is less than the target element X, we update the start pointer with middle→next.
- If the middle node value is greater than the element X, we update the last pointer to the middle node.
- We perform the above operations until the start node equals last node or the last node becomes NULL.
- Then we check if the node returned by the function is not NULL we print Element Found else we print Element not Found.
Dry Run

Code Implementation of Binary Search on Linked List
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
struct Node *newNode(int x)
{
struct Node* temp = (struct Node*)malloc(sizeof(struct Node));
temp->data = x;
temp->next = NULL;
return temp;
}
// function to find out middle element
struct Node* middle(struct Node* start,struct Node* last)
{
if (start == NULL)
return NULL;
struct Node* slow = start;
struct Node* fast = start -> next;
while (fast != last)
{
fast = fast -> next;
if (fast != last)
{
slow = slow -> next;
fast = fast -> next;
}
}
return slow;
}
// Function for implementing the Binary
// Search on linked list
struct Node* binarySearch(struct Node *head, int value)
{
struct Node* start = head;
struct Node* last = NULL;
do
{
// Find middle
struct Node* mid = middle(start, last);
// If middle is empty
if (mid == NULL)
return NULL;
// If value is present at middle
if (mid -> data == value)
return mid;
// If value is more than mid
else if (mid -> data < value)
start = mid -> next;
// If the value is less than mid.
else
last = mid;
} while (last == NULL ||
last != start);
// value not present
return NULL;
}
// Driver Code
int main()
{
struct Node *head = newNode(1);
head->next = newNode(4);
head->next->next = newNode(7);
head->next->next->next = newNode(8);
head->next->next->next->next = newNode(9);
head->next->next->next->next->next = newNode(10);
int value = 8;
if (binarySearch(head, value) == NULL)
printf("Value not present\n");
else
printf("Present");
return 0;
}
#include<bits stdc++.h="">
using namespace std;
struct Node
{
int data;
struct Node* next;
};
Node *newNode(int x)
{
struct Node* temp = new Node;
temp->data = x;
temp->next = NULL;
return temp;
}
struct Node* find_middle_node(Node* start, Node* last)
{
if (start == NULL){
return NULL;
}
struct Node* slow = start;
struct Node* fast = start -> next;
while (fast != last)
{
fast = fast -> next;
if (fast != last)
{
slow = slow -> next;
fast = fast -> next;
}
}
return slow;
}
struct Node* binarySearch(Node *head, int value){
struct Node* start = head;
struct Node* last = NULL;
do
{
Node* mid = find_middle_node(start, last);
if (mid == NULL){
return NULL;
}
if (mid -> data == value){
return mid;
}
else if (mid -> data < value){
start = mid -> next;
}
else{
last = mid;
}
} while (last == NULL ||
last != start);
return NULL;
}
int main()
{
Node *head = newNode(2);
head->next = newNode(5);
head->next->next = newNode(7);
head->next->next->next = newNode(11);
head->next->next->next->next = newNode(15);
head->next->next->next->next->next = newNode(18);
int value = 5;
if (binarySearch(head, value) == NULL)
printf("Element not Found\n");
else
printf("Element Found");
return 0;
}
class Node
{
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
class BinarySearch
{
static Node push(Node head, int data)
{
Node newNode = new Node(data);
newNode.next = head;
head = newNode;
return head;
}
static Node middleNode(Node start, Node last)
{
if (start == null)
return null;
Node slow = start;
Node fast = start.next;
while (fast != last)
{
fast = fast.next;
if (fast != last)
{
slow = slow.next;
fast = fast.next;
}
}
return slow;
}
static Node binarySearch(Node head, int value)
{
Node start = head;
Node last = null;
do
{
Node mid = middleNode(start, last);
if (mid == null)
return null;
if (mid.data == value)
return mid;
else if (mid.data > value)
{
start = mid.next;
}
else
last = mid;
} while (last == null || last != start);
return null;
}
public static void main(String[] args)
{
Node head = null;
head = push(head, 2);
head = push(head, 5);
head = push(head, 7);
head = push(head, 11);
head = push(head, 15);
head = push(head, 18);
int value = 7;
if (binarySearch(head, value) == null)
{
System.out.println("Element not found");
}
else
{
System.out.println("Element found");
}
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
self.prev = None
def newNode(x):
temp = Node(0)
temp.data = x
temp.next = None
return temp
def middle(start, last):
if (start == None):
return None
slow = start
fast = start . next
while (fast != last):
fast = fast . next
if (fast != last):
slow = slow . next
fast = fast . next
return slow
def binarySearch(head,value):
start = head
last = None
while True :
mid = middle(start, last)
if (mid == None):
return None
if (mid . data == value):
return mid
elif (mid . data < value):
start = mid . next
else:
last = mid
if not (last == None or last != start):
break
return None
head = newNode(2)
head.next = newNode(5)
head.next.next = newNode(7)
head.next.next.next = newNode(11)
head.next.next.next.next = newNode(15)
head.next.next.next.next.next = newNode(18)
value = 9
if (binarySearch(head, value) == None):
print("Element not Found\n")
else:
print("Element Found")
Output
Element Found
Time Complexity: O(n), where n is the total number of nodes in the Singly Linked List though we are performing a Binary search still in the worst case the complexity is O(n).
Conclusion
In this blog, we have covered the process of performing a binary search on linked list. Our experts are dedicated to providing you with a comprehensive selection of valuable information. For further mastery in linked lists, you can follow the link provided. We hope you will understand how to apply binary search on linked list.
## FAQs related to Binary Search on Linked List
- Can we do a binary search on linked list?
- Which search is best for the linked list?
- Linear search on unordered lists. Which takes O(N).
- Binary search is possible by using a skip list.
- Why is binary search faster than linear search?
Yes, binary search is possible on linked lists if the linked list is in an ordered format and we know the count of the nodes in the linked list.
You have two choices for applying search algorithms on linked lists:
Binary search is faster than linear search when the given array is already sorted.


