Last Updated on March 30, 2022 by Ria Pathak

Concepts Used
Breadth First Search
Difficulty Level
Easy
Problem Statement :
Given locations of
X&Yislands, we need to find the minimum distance between a given pair of islands(X,Y).
See original problem statement here
Solution Approach :
Introduction :
We can calculate distance between any two nodes by counting the number of edges between them. We can perform either Breadth First Search or Depth First Search to traverse each vertex of the graph.
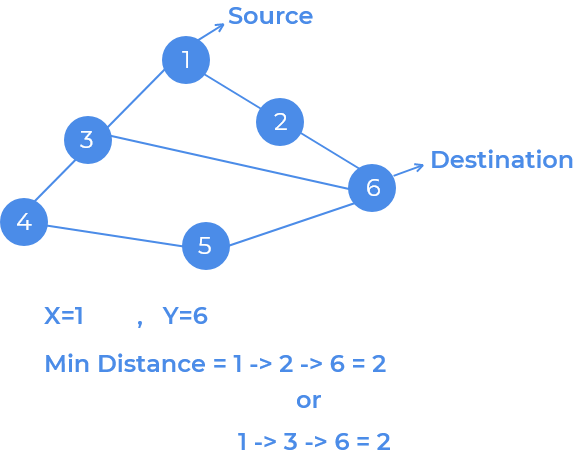
Description :
We are using Breadth First Search or BFS to find minimum number of edges between source (
s) & destination (d) vertex. We will maintain a distance[ ] array (initally 0), it will store the distance ofithvertex atithindex starting froms.
Starting froms, it is at distance 0 from itself, traverse all the vertex adjacent tosand update their distances(distance = distance[s] + 1), since each vertex is adjacent tosand at distance1from it, it will take(distance[s]+1)distance to reach them froms. Now consider all the vertices adjacent to the vertex adjacent tos. These are all at distance(distance[s]+2)fromsand so on.In this way, we will visit every non-visited vertex (
x) which is adjacent to some vertex (y) and store its distance asdistance[x]=distance[y]+1. Finally we can get the distance of our destination vertexdatdistance[d].
Algorithm :
Breadth First Search :
- Create a queue
qwhich will contain the vertices to be processed and a Boolean arrayvisited[](initally false, as no vertex has been visited yet) which indicates for each vertex, if it has been visited or not.- Initially, push the source
sto theqand setvisited[s]=true.- Then, loop until the queue is empty and in each iteration :
- pop a vertex (
x) from the front of the queue.
Iterate through all the adjacent verticesiof vertexxand if some of these verticesithat are not already visited (visited[i]=false), mark them as visited (visited[i]=true) and push them in the queue.- Stop when
qis empty.
Solutions:
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#define INT_MIN -9999
//ADJACENCY LIST
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
};
// Create a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Create a graph
struct Graph* createAGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
int i;
for (i = 0; i < vertices; i++)
graph->adjLists[i] = NULL;
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int s, int d) {
// Add edge from s to d
struct node* newNode = createNode(d);
newNode->next = graph->adjLists[s];
graph->adjLists[s] = newNode;
// Add edge from d to s
newNode = createNode(s);
newNode->next = graph->adjLists[d];
graph->adjLists[d] = newNode;
}
//QUEUE
struct Queue
{
int front, rear, size;
unsigned capacity;
int* array;
};
// function to create a queue of given capacity.
// It initializes size of queue as 0
struct Queue* createQueue(unsigned capacity)
{
struct Queue* queue = (struct Queue*) malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1; // This is important, see the enqueue
queue->array = (int*) malloc(queue->capacity * sizeof(int));
return queue;
}
// Queue is empty when size is 0
int isEmpty(struct Queue* queue)
{ return (queue->size == 0); }
// Function to add an item to the queue.
// It changes rear and size
void enqueue(struct Queue* queue, int item)
{
queue->rear = (queue->rear + 1)%queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
}
// Function to remove an item from queue.
// It changes front and size
int dequeue(struct Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
int item = queue->array[queue->front];
queue->front = (queue->front + 1)%queue->capacity;
queue->size = queue->size - 1;
return item;
}
// Function to get front of queue
int front(struct Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
return queue->array[queue->front];
}
int minEdgeBFS( struct Graph* graph, int u,int v, int n)
{
// visited[n] for keeping track of visited
// node in BFS
int distance[n+1];
int visited[n+1];
memset(visited, 0, sizeof(visited));
memset(distance, 0, sizeof(distance));
// Initialize distances as 0
// queue to do BFS.
struct Queue* Q = createQueue(100);
distance[u] = 0;
enqueue(Q,u);
visited[u] = 1;
while (!isEmpty(Q))
{
int x = dequeue(Q);
struct node * temp = graph->adjLists[x];
while(temp)
{
//break;
if (!visited[temp->vertex])
{
distance[temp->vertex] = distance[x] + 1;
enqueue(Q,temp->vertex);
visited[temp->vertex] = 1;
}
temp = temp->next;
}
}
return distance[v];
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m,u,v;
scanf("%d %d",&n,&m);
struct Graph* graph = createAGraph(n);
while(m-->0)
{
int a,b;
scanf("%d %d",&a,&b);
addEdge(graph,a,b);
}
scanf("%d %d",&u,&v);
printf("%d\n",minEdgeBFS(graph, u, v, n));
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
int minEdgeBFS(vector <int> edges[], int u,int v, int n)
{
vector<bool> visited(n, 0);
// Initialize distances as 0
vector<int> distance(n, 0);
// queue to do BFS.
queue <int> Q;
distance[u] = 0;
Q.push(u);
visited[u] = true;
while (!Q.empty())
{
int x = Q.front();
Q.pop();
for (int i=0; i<edges[x].size(); i++)
{
if (visited[edges[x][i]])
continue;
// update distance for i
distance[edges[x][i]] = distance[x] + 1;
Q.push(edges[x][i]);
visited[edges[x][i]] = 1;
}
}
return distance[v];
}
void addEdge(vector <int> edges[], int u, int v)
{
edges[u].push_back(v);
edges[v].push_back(u);
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n,m,u,v;
cin>>n>>m;
vector <int> edges[n];
while(m--)
{
int a,b;
cin>>a>>b;
addEdge(edges, a,b);
}
cin>>u>>v;
cout << minEdgeBFS(edges, u, v, n)<<endl;
}
return 0;
}
import java.util.*;
class Main
{
static int minEdgeBFS(Vector <Integer> edges[], int u,int v, int n)
{
Vector<Boolean> visited = new Vector<Boolean>(n);
for (int i = 0; i < n; i++) {
visited.addElement(false);
}
// Initialize distances as 0
Vector<Integer> distance = new Vector<Integer>(n);
for (int i = 0; i < n; i++) {
distance.addElement(0);
}
// queue to do BFS.
Queue<Integer> Q = new LinkedList<>();
distance.setElementAt(0, u);
Q.add(u);
visited.setElementAt(true, u);
while (!Q.isEmpty())
{
int x = Q.peek();
Q.poll();
for (int i=0; i<edges[x].size(); i++)
{
if (visited.elementAt(edges[x].get(i)))
continue;
// update distance for i
distance.setElementAt(distance.get(x) + 1 , edges[x].get(i));
Q.add(edges[x].get(i));
visited.setElementAt(true,edges[x].get(i));
}
}
return distance.get(v);
}
// method for addition of edge
static void addEdge(Vector <Integer> edges[], int u,int v)
{
edges[u].add(v);
edges[v].add(u);
}
// Driver method
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-->0)
{
int n = sc.nextInt();
int e = sc.nextInt();
Vector <Integer> edges[] = new Vector[n];
for (int i = 0; i < edges.length; i++) {
edges[i] = new Vector<>();
}
while(e-->0)
{
int u = sc.nextInt();
int v = sc.nextInt();
addEdge(edges, u, v);
}
int u = sc.nextInt();
int v = sc.nextInt();
System.out.println(minEdgeBFS(edges, u, v, n));
}
}
}
Space Complexity is O(V) as it requires two arrays (dist[ ] & visited[ ]) of size V.
[forminator_quiz id="2123"]
This article tried to discuss the concept of Breadth First Search. Hope this blog helps you understand and solve the problem. To practice more problems on Breadth First Search you can check out MYCODE | Competitive Programming.


