Last Updated on June 28, 2022 by Ria Pathak

Skew Heap:
So basically, Skew Heap is a heap data structure implemented as a binary tree. Skew Heap has an advantage over binary trees as skew heaps merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied :
- In general, heap order must be there i.e. the value of the root node should be minimum and the same for the children of the root node, but a complete tree is not necessary.
- The main operation in the skew heap is merged, Also we can implement other operations too like insertion, extractMin, and so on using merge only.
A skew heap is a self-adjusting form of a heap.
Properties of a skew heap:
- A Heap that contains only one element is a skew heap.
- The result of merging two heaps will be a skew heap.

Recursive Merge Approach:
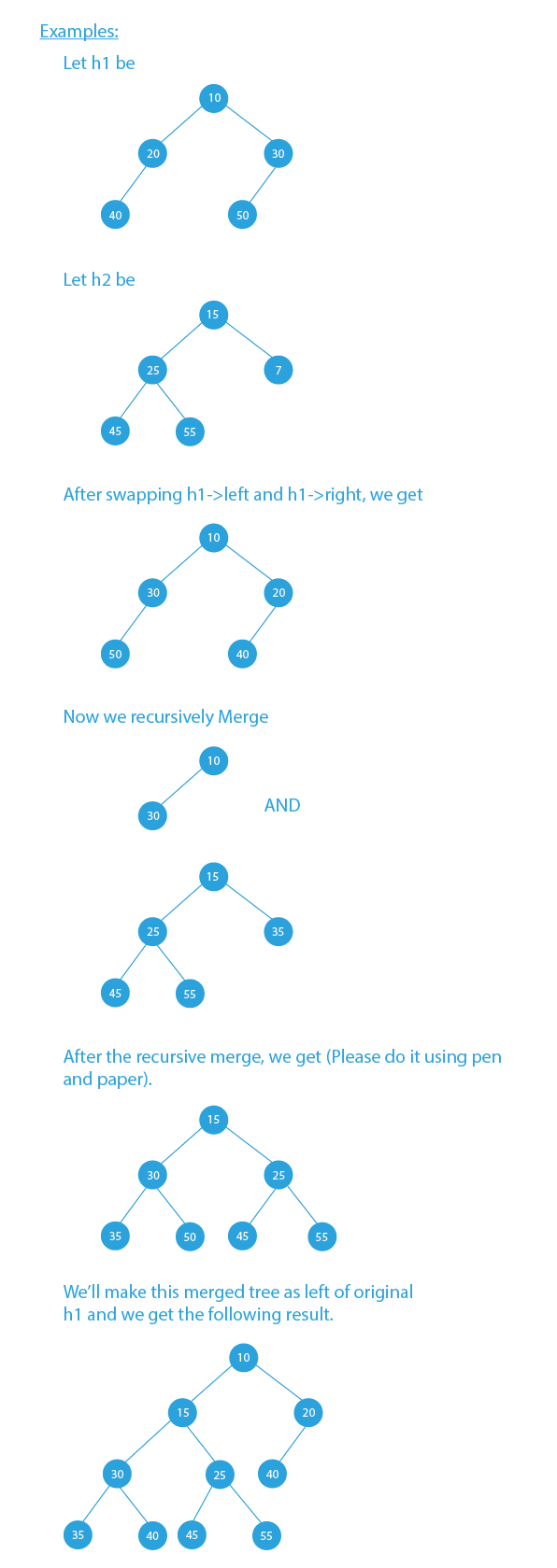
- We’ll merge h1 and h2.
- Let h1 be the first skew heap and h2 be the second skew heap, in this example, we are assuming that the root of h1 is smaller than the root of h2.
- Swap h1->left with h2->right.
- Call the recursive function i.e. h1->left = merge(h2,h1->left).
Code Implementation
#includeusing namespace std; struct SkewHeap { int key; SkewHeap* right; SkewHeap* left; SkewHeap() { key = 0; right = NULL; left = NULL; } SkewHeap* merge(SkewHeap* h1, SkewHeap* h2) { if (h1 == NULL) return h2; if (h2 == NULL) return h1; if (h1->key > h2->key) swap(h1, h2); swap(h1->left, h1->right); h1->left = merge(h2, h1->left); return h1; } SkewHeap* construct(SkewHeap* root, int heap[], int n) { SkewHeap* temp; for (int i = 0; i < n; i++) { temp = new SkewHeap; temp->key = heap[i]; root = merge(root, temp); } return root; } void inorder(SkewHeap* root) { if (root == NULL) return; else { inorder(root->left); cout << root->key << " "; inorder(root->right); } return; } }; int main() { SkewHeap heap, *temp1 = NULL, *temp2 = NULL; int heap1[] = { 12, 5, 10 }; int heap2[] = { 3, 7, 8, 14}; int n1 = sizeof(heap1) / sizeof(heap1[0]); int n2 = sizeof(heap2) / sizeof(heap2[0]); temp1 = heap.construct(temp1, heap1, n1); temp2 = heap.construct(temp2, heap2, n2); temp1 = heap.merge(temp1, temp2); cout << "Merged Heap is: " << endl; heap.inorder(temp1); }
This article tried to discuss the Implementation of skew heap. Hope this blog helps you understand the concept. To practice problems on Heap you can check out MYCODE | Competitive Programming – Heaps at Prepbytes


