Last Updated on November 8, 2022 by Prepbytes

Introduction
In the article, we will learn to add 1 to a number represented as linked list.As we know a linked list is a linear data structure. In a linked list, the elements are linked using pointers and each node points to the next node. Let’s try to understand how we can 1 to a number represented as linked list.
Problem Statement
In this problem, we are given a number represented in the form of a linked list, we are required to add 1 to it and report the answer as a linked list.
For Example: Given is a Number 19999 in the form of a linked list, and after adding 1 to linked list, it should give the result as follows:


Problem Statement Understanding to add 1 to linked list
The problem statement is quite straightforward, we are provided with a number represented in the form of a linked list which means we will be getting the head/root of the linked list as our argument, and we have to add 1 to the number represented as linked list.
Let’s learn programming languages online and try to understand to add 1 to linked list more clearly using an example.
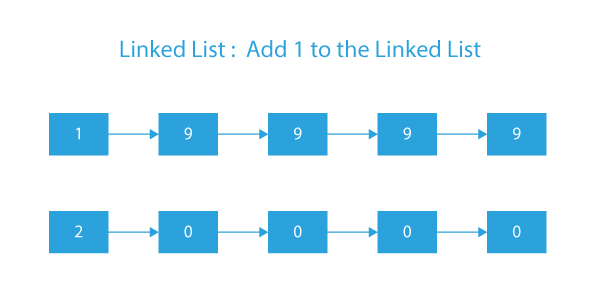
Let’s assume we are given the number 19999. So the linked list will be :
- Initial Linked List: 1 → 9 → 9 → 9 → 9
- We will be getting the head pointing to the 1st node of the linked list, which is 1 as our argument.
- So the head pointer will point to the first node:
head →1 → 9 → 9 → 9 → 9 - After we add 1 to linked list, our linked list will become:
head →2 → 0 → 0 → 0 → 0 - Which is the result after adding 1 to 19999 = 20000
At this point in time, we have understood how to add 1 to a number represented as linked list. Now try to formulate an approach to add 1 to a number represented as linked list.
Helpful Observation to add 1 to linked list
- Since we do an arithmetic operation starting from the one’s place digit and then move towards the tenth place digit, hundredth place digit and so on, therefore we need to get hold of the one’s place digit to add 1 to linked list.
- Now the one’s place digit is the last digit of our number given in the form of a linked list. But we cannot move backside in the linked list, as only the next pointer is given.
- So we can reverse the linked list and do operations starting from the first node of the reversed linked list.
- So, our original linked list will be reversed and thus we can now simply add 1 to the head of the linked list (maintaining carry). Finally, we will reverse the list again and will output it as our final linked list.
Approach and Algorithm to add 1 to linked list
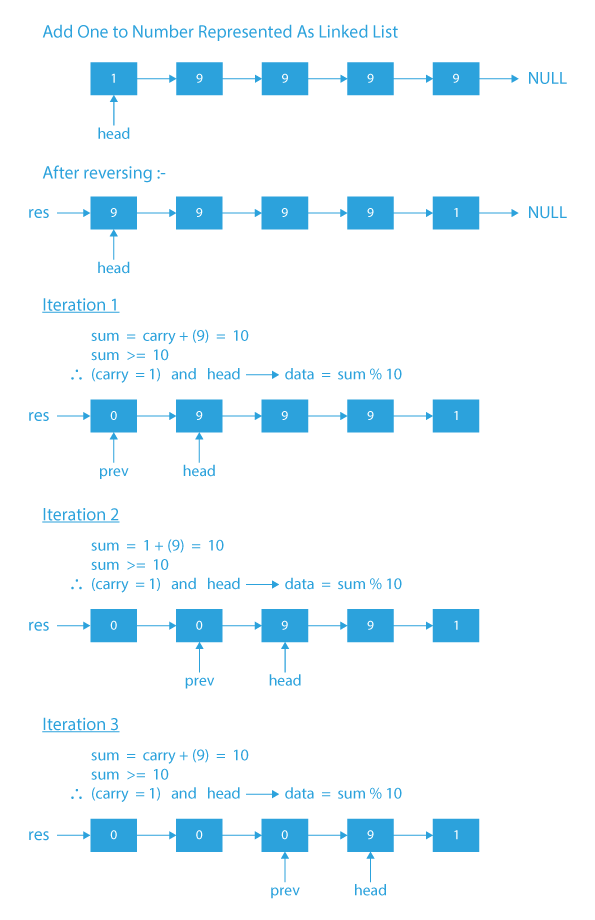
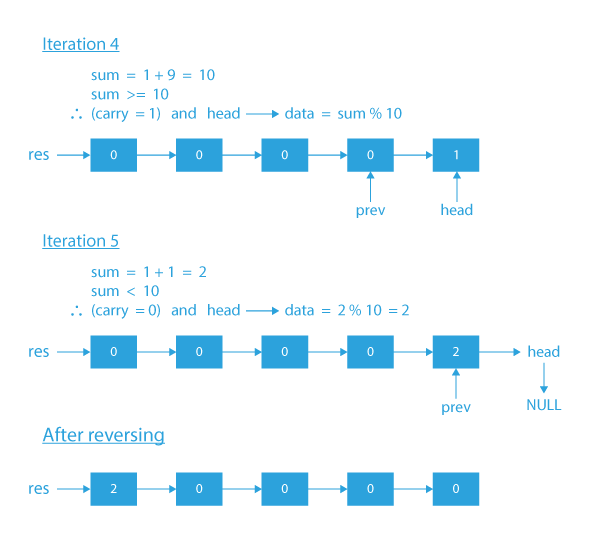
- Reverse the given Linked List. For example, the given linked list is 1 → 9 → 9 → 9 → 9, after reversing it will become 9 → 9 → 9 → 9 → 1.
- Start the linked list traversal, take 2 variable sum and carry.
- The variable sum will hold the value at a particular place (node) and carry will take forward the carry from the previous sum given by (sum/10).
- Now, since we need to add 1 to linked list, the sum can be either equal than 10 or less than 10.
- Therefore, carry will be 1 for a sum greater than 10 and 0 for a sum less than 10.
- Keep moving forward in the list and store the appropriate value in the resultant list node given by sum%10.
- At last, again reverse the linked list to get the output in the correct format.
Dry Run to add 1 to linked list
For addOne Function
Code Implementation to add 1 to linked list
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
struct Node* prev;
};
/* Function to create a new node with given data */
struct Node *newNode(int data)
{
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->data = data;
new_node->next = NULL;
return new_node;
}
/* Function to reverse the linked list */
struct Node *reverse(struct Node *head)
{
struct Node * prev = NULL;
struct Node * current = head;
struct Node * next;
while (current != NULL)
{
next = current->next;
current->next = prev;
prev = current;
current = next;
}
return prev;
}
/* Adds one to a linked lists and return the head
node of resultant list */
struct Node *addOneUtil(struct Node *head)
{
// res is head node of the resultant list
struct Node* res = head;
struct Node *temp;
struct Node* prev = NULL;
int carry = 1, sum;
while (head != NULL) //while both lists exist
{
// Calculate value of next digit in resultant list.
// The next digit is sum of following things
// (i) Carry
// (ii) Next digit of head list (if there is a
// next digit)
sum = carry + head->data;
// update carry for next calculation
carry = (sum >= 10)? 1 : 0;
// update sum if it is greater than 10
sum = sum % 10;
// Create a new node with sum as data
head->data = sum;
// Move head and second pointers to next nodes
temp = head;
head = head->next;
}
// if some carry is still there, add a new node to
// result list.
if (carry > 0)
temp->next = newNode(carry);
// return head of the resultant list
return res;
}
// This function mainly uses addOneUtil().
struct Node* addOne(struct Node *head)
{
// Reverse linked list
head = reverse(head);
// Add one from left to right of reversed
// list
head = addOneUtil(head);
// Reverse the modified list
return reverse(head);
}
// A utility function to print a linked list
void printList(struct Node *node)
{
while (node != NULL)
{
printf("%d", node->data);
node = node->next;
}
printf("\n");
}
/* Driver program to test above function */
int main(void)
{
struct Node *head = newNode(1);
head->next = newNode(9);
head->next->next = newNode(9);
head->next->next->next = newNode(9);
printf("List is ");
printList(head);
head = addOne(head);
printf("\nResultant list is ");
printList(head);
return 0;
}
#include<bits stdc++.h="">
using namespace std;
class Node
{
public:
int data;
Node *next;
Node(int val) {
data = val;
next = NULL;
}
};
Node* addOne(Node* head_ref)
{
Node* res = head_ref; // res will point to the head of the resultant list.
int carry = 1 , sum;//Why carry is taken as 1 ? => because we need to add 1
Node* prev; // prev pointer is necessary for the last node, if at last carry is there, we need to add a new Node with value carry.
// (Take example of 9->9->9->9)
while (head_ref != NULL) {
sum = carry + head_ref->data;
carry = (sum >= 10) ? 1 : 0;
head_ref->data = (sum % 10);
prev = head_ref;
head_ref = head_ref->next;
}
if (carry > 0) {
prev->next = new Node(carry);
}
return res;
}
Node* reverseList(Node* head_ref) {
Node* curr = head_ref;
Node* prev = NULL, *next;
while (curr != nullptr) {
next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
Node* addOneToList(Node* head_ref)
{
head_ref = reverseList(head_ref);
head_ref = addOne(head_ref);
head_ref = reverseList(head_ref);
return head_ref;
}
void printList(Node *node)
{
while (node != NULL)
{
cout << node->data << " ";
node = node->next;
}
}
int main()
{
Node* head = new Node(1);
head->next = new Node(9);
head->next->next = new Node(9);
head->next->next->next = new Node(9);
head->next->next->next->next = new Node(9);
head = addOneToList(head);
printList(head);
return 0;
}
class CarryOne {
/* Linked list node */
static class Node
{
int data;
Node next;
}
/* Function to create a new node with given data */
static Node newNode(int data)
{
Node new_node = new Node();
new_node.data = data;
new_node.next = null;
return new_node;
}
static int addWithCarry(Node head)
{
if (head == null)
return 1;
// Add carry returned be next node call
int res = head.data + addWithCarry(head.next);
// Update data and return new carry
head.data = (res) % 10;
return (res) / 10;
}
// This function mainly uses addWithCarry().
static Node addOne(Node head)
{
int carry = addWithCarry(head);
// If there is carry after processing all nodes,
// then we need to add a new node to linked list
if (carry > 0)
{
Node newNode = newNode(carry);
newNode.next = head;
return newNode; // New node becomes head now
}
return head;
}
// A utility function to print a linked list
static void printList(Node node)
{
while (node != null)
{
System.out.print(node.data);
node = node.next;
}
System.out.println();
}
/* Driver code */
public static void main(String[] args)
{
Node head = newNode(1);
head.next = newNode(2);
head.next.next = newNode(2);
System.out.print("List is ");
printList(head);
head = addOne(head);
System.out.println();
System.out.print("Resultant list is ");
printList(head);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(data):
return Node(data)
def reverseList(head):
if not head:
return
curNode = head
prevNode = head
nextNode = head.next
curNode.next = None
while(nextNode):
curNode = nextNode
nextNode = nextNode.next
curNode.next = prevNode
prevNode = curNode
return curNode
def addOne(head):
head = reverseList(head)
k = head
carry = 0
prev = None
head.data += 1
while(head != None) and (head.data > 9 or carry > 0):
prev = head
head.data += carry
carry = head.data // 10
head.data = head.data % 10
head = head.next
if carry > 0:
prev.next = Node(carry)
return reverseList(k)
def printList(head):
if not head:
return
while(head):
print("{}".format(head.data), end=" ")
head = head.next
if __name__ == '__main__':
head = newNode(1)
head.next = newNode(9)
head.next.next = newNode(9)
head.next.next.next = newNode(9)
head = addOne(head)
printList(head)
Output
2 → 0 → 0 → 0 → 0
Time Complexity: O(n), Overall we are doing a total of 3 passes, 2 for reversing and 1 while adding, where n is the number of nodes in the given LinkedList.
Space complexity: O(1), constant space complexity, as no extra space is used.
Can we Do Any Better ?
- Now we have seen that for the above approach to work to add 1 to a number represented as linked list, we need to reverse the list twice. So we are doing two extra traversals worth O(N) complexity.
- However, if we observe carefully, we will see that it is the digit 9 which makes all the changes, for all other digits we just need to increment by 1. But in the case of 9 carry comes into the picture and modifies the whole list.
- So, we can try targeting the digit 9 itself. We don’t need to reverse the linked list.
Approach and Algorithm to add 1 to linked list
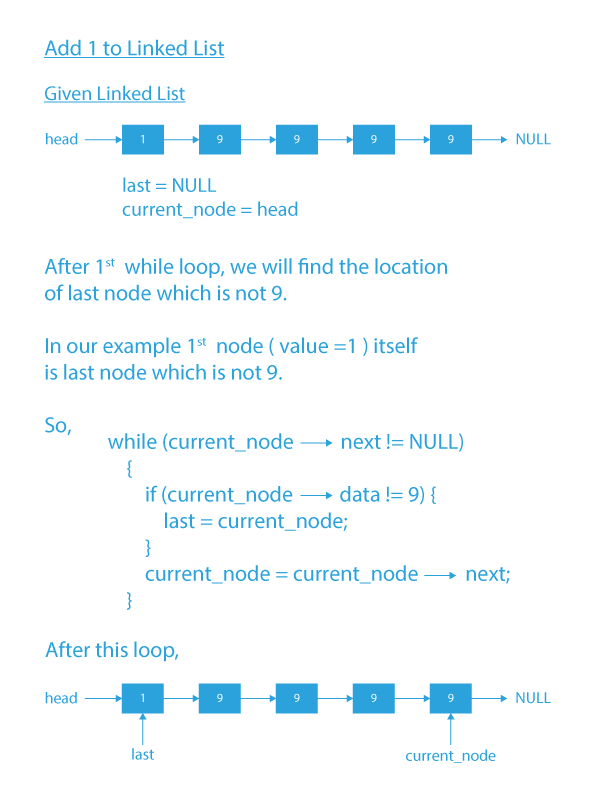
We will find the last node which is not 9. Now for this, there can be 3 scenarios to add q to linked list:
- Case1: If there exists no node which is not 9, it means every node is 9. For example 9->9->9->9. In such a case we will make every node value equal to 0 and add a new node with value 1 at the front of the list.
- Case2: If the last node of the list is not 9, then simply increment the value of the last node by 1.
- Case3: If the node which is not 9 is somewhere in the middle, and after that, every node is 9. For example 1299, then in such cases increment the last non-nine node by 1 and make all nodes right to it as zero. So 1299 becomes 1300.
We will take 2 pointers, one for storing the last node which is not 9, other for traversing the list. Then handle each case independently.
Dry Run to add 1 to linked list
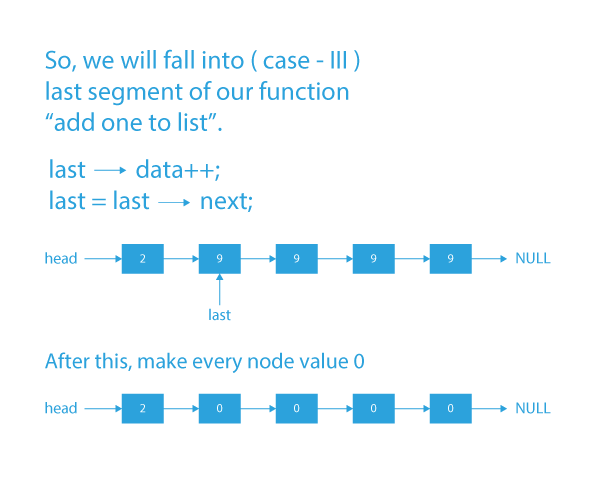
Code Implementation to add 1 to linked list
#include<stdio.h>
#include<stdlib.h>
struct Node {
int data;
struct Node* next;
};
/* Function to create a new node with given data */
struct Node* newNode(int data)
{
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));;
new_node->data = data;
new_node->next = NULL;
return new_node;
}
int addWithCarry(struct Node* head)
{
// If linked list is empty, then
// return carry
if (head == NULL)
return 1;
// Add carry returned be next node call
int res = head->data + addWithCarry(head->next);
// Update data and return new carry
head->data = (res) % 10;
return (res) / 10;
}
struct Node* addOne(struct Node* head)
{
// Add 1 to linked list from end to beginning
int carry = addWithCarry(head);
// If there is carry after processing all nodes,
// then we need to add a new node to linked list
if (carry) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = carry;
newNode->next = head;
return newNode; // New node becomes head now
}
return head;
}
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d", node->data);
node = node->next;
}
printf("\n");
}
/* Driver code */
int main(void)
{
struct Node* head = newNode(1);
head->next = newNode(9);
head->next->next = newNode(9);
head->next->next->next = newNode(9);
printf("List is ");
printList(head);
head = addOne(head);
printf("\nResultant list is ");
printList(head);
return 0;
}
#include<bits stdc++.h="">
using namespace std;
class Node
{
public:
int data;
Node *next;
Node(int val) {
data = val;
next = NULL;
}
};
void printList(Node *node)
{
while (node != NULL)
{
cout << node->data << " ";
node = node->next;
}
}
Node* addOneToList(Node* head)
{
Node* last = NULL , *current_node = head;
//Through this loop we will find the last non-nine node.
while (current_node->next != NULL)
{
if (current_node->data != 9) {
last = current_node;
}
current_node = current_node->next;
}
//This loop will run till the second last node, so for the last node we will check using if condition.
//If the last node itself is not 9. Then simply increment the value by 1 and return the head.
if (current_node->data != 9) {
current_node->data++;
return head;
}
//After loop if last is still NULL, that means there is no value which is not 9.
//For example 9->9->9->9
if (last == NULL) {
//1 extra node will be needed.
last = new Node(1);
last->next = head;
head = last;
//then make every node 0
last = last->next;
while (last != NULL) {
last->data = 0;
last = last->next;
}
return head;
}
//Last case => when the non-nine node is somewhere in middle;
// we will increment the value and make everything right to it as 0
last->data++;
last = last->next;
while (last != NULL) {
last->data = 0;
last = last->next;
}
return head;
}
int main()
{
Node* head = new Node(1);
head->next = new Node(9);
head->next->next = new Node(9);
head->next->next->next = new Node(9);
head->next->next->next->next = new Node(9);
head = addOneToList(head);
printList(head);
return 0;
}
class CarryOne{
static class Node
{
int data;
Node next;
}
static Node newNode(int data)
{
Node new_node = new Node();
new_node.data = data;
new_node.next = null;
return new_node;
}
static Node addOne(Node head)
{
Node last = null ;
Node current_node = head;
//Through this loop we will find the last non-nine node.
while (current_node.next != null)
{
if (current_node.data != 9) {
last = current_node;
}
current_node = current_node.next;
}
//This loop will run till the second last node, so for the last node we will check using if condition.
//If the last node itself is not 9. Then simply increment the value by 1 and return the head.
if (current_node.data != 9) {
current_node.data=current_node.data+1;
return head;
}
//After loop if last is still NULL, that means there is no value which is not 9.
//For example 9->9->9->9
if (last == null) {
//1 extra node will be needed.
last = newNode(1);
last.next = head;
head = last;
//then make every node 0
last = last.next;
while (last != null) {
last.data = 0;
last = last.next;
}
return head;
}
//Last case => when the non-nine node is somewhere in middle;
// we will increment the value and make everything right to it as 0
last.data=last.data+1;
last = last.next;
while (last != null) {
last.data = 0;
last = last.next;
}
return head;
}
// A utility function to print a linked list
static void printList(Node node)
{
while (node != null)
{
System.out.print(node.data);
node = node.next;
}
System.out.println();
}
// Driver code
public static void main(String[] args)
{
Node head = newNode(1);
head.next = newNode(2);
head.next.next = newNode(2);
System.out.print("List is ");
printList(head);
head = addOne(head);
System.out.println();
System.out.print("Resultant list is ");
printList(head);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(data):
return Node(data)
def printList(head):
if not head:
return
while(head):
print("{}".format(head.data), end=" ")
head = head.next
def addOneToList(head):
last = None
current_node = head
# Through this loop we will find the last non-nine node
while current_node.next:
if current_node.data != 9:
last = current_node
current_node = current_node.next
# This loop will run till the second last node, so for the last node we will check using if condition.
# If the last node itself is not 9. Then simply increment the value by 1 and return the head.
if current_node.data != 9:
current_data.data += 1
return head
# After loop if last is still NULL, that means there is no value which is not 9
# For example 9->9->9->9
if last == None:
# 1 extra node will be needed.
last = newNode(1)
last.next = head
head = last
# then make every node 0
last = last.next
while last != None:
last.data = 0
last = last.next
return head
# Last case => when the non-nine node is somewhere in middle;
# we will increment the value and make everything right to it as 0
last.data += 1
last = last.next
while last:
last.data = 0
last = last.next
return head
if __name__ == '__main__':
head = newNode(1)
head.next = newNode(9)
head.next.next = newNode(9)
head.next.next.next = newNode(9)
head.next.next.next.next = newNode(9)
head = addOneToList(head)
printList(head)
Output
2 → 0 → 0 → 0 → 0
Time Complexity: O(n) only single pass, where n is the number of nodes in the given LinkedList.
[forminator_quiz id=”4441″]
In this article we have explained how to add 1 to a number represented as linked list. We have explained different approaches with a pictorial dry run and code implementation with time and space complexities as well. To learn more about the linked list you can follow this link Linked List.
Footer
FAQs to add 1 to linked list
- What is the time complexity to count the number of elements in a linked list?
- What are the basic operations that can be performed in a linked list?
- Which operation is not supported by the linked list?
To count the number of elements, you have to traverse through a linked list and it will take O(n) time.
We can do traversal, insertion, deletion, searching, updating, sorting and merging in the linked list.
Circulate is not supported by a linked list as a linked list is a linear collection of data elements whose order is not given by their physical placement in memory.


