Last Updated on November 25, 2022 by Prepbytes

In this blog, we will see a linked list problem ”square root of nth node of linked list”. Linked lists play a major role in the placements and having a good grasp of Linked Lists can be a huge plus point in a coding interview.
How to find square root of nth node of linked list
We have been given a linked list in this problem. Our task is to write a function that accepts the head node of the linked list as a parameter and returns the value of the node present at (floor(sqrt(n)))th position in the linked list.
Here n is the count of the number of nodes present in the linked list.
Let’s try to understand the problem with help of examples by referring to online coding classes.
Suppose we are given a linked list A → B → C → D → E → F and now according to the problem statement we have to find the node at (floor(sqrt(n)))th position in the linked list and return its value as output.
For the above given linked list n = 6, as there are 6 nodes in the linked list, so
- (floor(sqrt(n))) = floor(sqrt(6)) = 2, it means that we have to return the value of 2nd node of the linked list as output.
Output: B
Explanation: We will return B in output as B is the value of (floor(sqrt(n)))th node of the above given linked list.
If the linked list is:

For the above linked list n = 9 (as there are 9 nodes in the linked list), then the value of (floor(sqrt(n))) is:
- (floor(sqrt(n))) = (floor(sqrt(9))) = 3, so we will return the value of 3rd node of the linked list as output.
Output: C
Note: Here in this problem we are considering 1 based indexing.
Some more Examples:
Input :

Output : 3
Input :

Output : 60
Input :

Output : 14
Now I think from the above examples the problem is clear, and now we have to think about how we can approach it.
Approach 1 of the square root of nth node of linked list
A simple approach is:
- First, loop through the linked list to find the number of nodes n in the linked list.
- Then calculate the value of floor(sqrt(n)), where n is the total number of nodes in the linked list.
- Now starting from the first node of the list traverse to this position given by floor(sqrt(n)) and return the data of the node at this position.
Time Complexity of the square root of nth node of linked list : O(n), as we are traversing the complete length of the list
Space Complexity of the square root of nth node of linked list: O(1).
This approach traverses the linked list 2 times. Let’s try to think, can we do better than this? Can we find out the (floor(sqrt(n)))th node of the linked list in one single traversal?
Let’s see approach 2 to get the answers to the above questions.
Approach 2 of the square root of nth node of linked list
As we know that:
- sqrt(1) = 1
- sqrt(4) = 2
- sqrt(9) = 3
- sqrt(16) = 4 ……….
One little conclusion which we can make about floor(sqrt(n)) is that:
- Every number in range from 1 to 3 will have floor(sqrt(n)) equal to 1.
- Every number in range from 4 to 8 will have floor(sqrt(n)) equal to 2.
- Similarly, every number in range from 9 to 15 will have floor(sqrt(n)) equal to 3.
- It goes on like this for range of numbers between every consequtive perfect squares.
Note: The final conclusion is that every number num between two consequtive perfect squares (a,b) (excluding the bigger perfect square b) have (floor(sqrt(num))) = sqrt(a).
Now we will try to utilize the above conclusion to solve this problem, and it will help us to find the (floor(sqrt(n)))th node of the linked list in single traversal.
The complete algorithm for this approach is explained below.
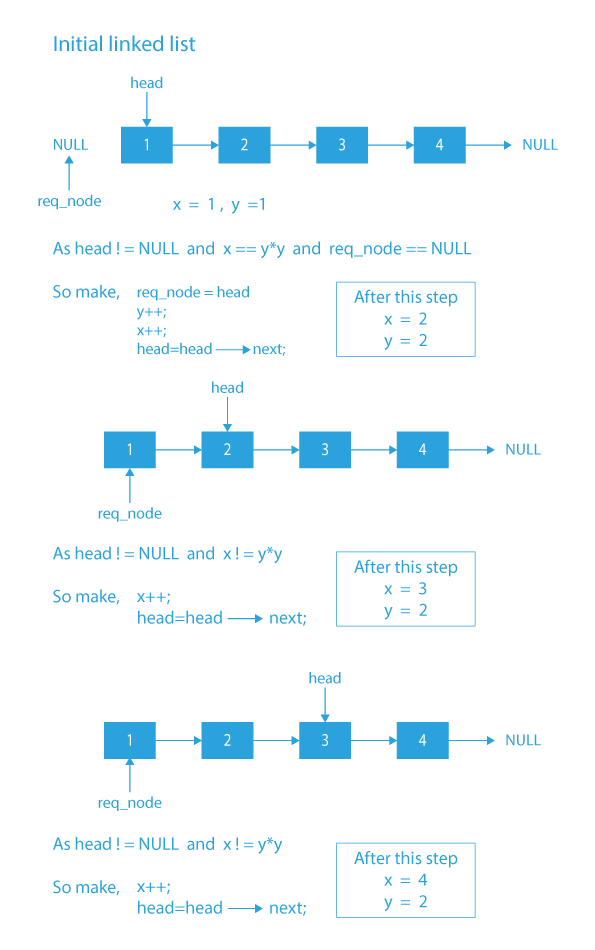
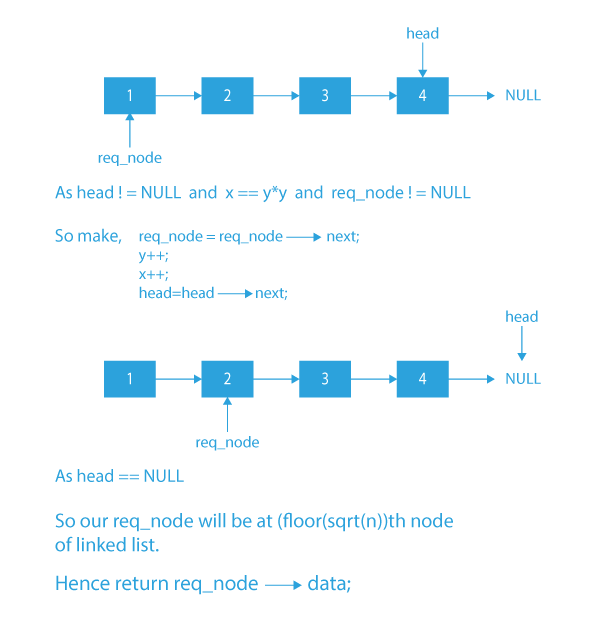
Algorithm of the square root of nth node of linked list
- Firstly, we will initialize 2 pointers x and y both to 1 and a pointer req_node to NULL to traverse till the required position in the list is reached.
- We will start traversing the list using the head node until the last node is reached.
- While traversing the list, we will check if the value of y is equal to sqrt(x).
- If the value is equal,we will increment both x and y by 1 and make req_node to req_node->next.
- Otherwise, we will increment only x.
- Now, when we reach the last node of the list x will contain the value of n, y will contain the value of sqrt(x) and req_node will point to the node at yth position.
- Finally, we will return the data contained in the node pointed by pointer req_node.
Dry Run of the square root of nth node of linked list
## Code Implementation of the square root of nth node of linked list
#include<stdio.h>
#include<stdlib.h>
// Linked list node
struct Node
{
int data;
struct Node* next;
};
// Function to get the sqrt(n)th
// node of a linked list
int printsqrtn(struct Node* head)
{
struct Node* sqrtn = NULL;
int i = 1, j = 1;
// Traverse the list
while (head!=NULL)
{
// check if j = sqrt(i)
if (i == j*j)
{
// for first node
if (sqrtn == NULL)
sqrtn = head;
else
sqrtn = sqrtn->next;
// increment j if j = sqrt(i)
j++;
}
i++;
head=head->next;
}
// return node's data
return sqrtn->data;
}
void print(struct Node* head)
{
while (head != NULL)
{
printf("%d ", head->data);
head = head->next;
}
printf("\n");
}
// function to add a new node at the
// beginning of the list
void push(struct Node** head_ref, int new_data)
{
// allocate node
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
// put in the data
new_node->data = new_data;
// link the old list off the new node
new_node->next = (*head_ref);
// move the head to point to the new node
(*head_ref) = new_node;
}
/* Driver program to test above function*/
int main()
{
/* Start with the empty list */
struct Node* head = NULL;
push(&head, 40);
push(&head, 30);
push(&head, 20);
push(&head, 10);
printf("Given linked list is:");
print(head);
printf("sqrt(n)th node is %d ",printsqrtn(head));
return 0;
}
#include <bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node* next;
};
int printsqrtn(Node* head)
{
Node* req_node = NULL;
int x = 1, y = 1;
while (head!=NULL)
{
if (x == y*y)
{
if (req_node == NULL)
req_node = head;
else
req_node = req_node->next;
y++;
}
x++;
head=head->next;
}
return req_node->data;
}
void printList(Node* head)
{
while (head != NULL)
{
cout << head->data << " ";
head = head->next;
}
cout<<endl;
}
void push(Node** head_ref, int new_data)
{
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int main()
{
Node* head = NULL;
push(&head, 4);
push(&head, 3);
push(&head, 2);
push(&head, 1);
cout << "Given linked list is: ";
printList(head);
cout << "sqrt(n)th node is " << printsqrtn(head);
return 0;
}
class SquareRoot
{
static class Node
{
int data;
Node next;
}
static Node head = null;
// Function to get the sqrt(n)th node of a linked list
static int printsqrtn(Node head)
{
Node sqrtn = null;
int i = 1, j = 1;
// Traverse the list
while (head != null)
{
// check if j = sqrt(i)
if (i == j * j)
{
// for first node
if (sqrtn == null)
sqrtn = head;
else
sqrtn = sqrtn.next;
// increment j if j = sqrt(i)
j++;
}
i++;
head=head.next;
}
return sqrtn.data;
}
static void print(Node head)
{
while (head != null)
{
System.out.print( head.data + " ");
head = head.next;
}
System.out.println();
}
static void push( int new_data)
{
Node new_node = new Node();
new_node.data = new_data;
new_node.next = head;
head = new_node;
}
/* Driver code*/
public static void main(String[] args)
{
push( 40);
push( 30);
push( 20);
push( 10);
System.out.print("Given linked list is:");
print(head);
System.out.print("sqrt(n)th node is " +printsqrtn(head));
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def printsqrtn(head) :
sqrtn = None
i = 1
j = 1
while (head != None) :
if (i == j * j) :
if (sqrtn == None) :
sqrtn = head
else:
sqrtn = sqrtn.next
j = j + 1
i = i + 1
head = head.next
return sqrtn.data
def print_1(head) :
while (head != None) :
print( head.data, end = " ")
head = head.next
print(" ")
def push(head_ref, new_data) :
new_node = Node(0)
new_node.data = new_data
new_node.next = (head_ref)
(head_ref) = new_node
return head_ref
if __name__=='__main__':
head = None
head = push(head, 4)
head = push(head, 3)
head = push(head, 2)
head = push(head, 1)
print("Given linked list is:")
print_1(head)
print("sqrt(n)th node is ", printsqrtn(head))
Output
Given linked list is: 1 2 3 4
sqrt(n)th node is 2
Time Complexity of the square root of nth node of linked list : O(n), as we are traversing the complete length of the list.
**Conclusion**
So, in this article, you have learned how to the square root of nth node of linked list. Also, you can solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.
## FAQs on the square root of nth node of linked list
**1. What is getNode and Freenode?**
We have a getnode() function that creates an empty. node for us. We have a freenode() function that deallocates the. memory pointed to by p.
**2. What is the meaning of Freenode?**
Freenode, stylized as Freenode and formerly known as Open Projects Network, is an IRC network that was previously used to discuss peer-directed projects. Their servers are accessible from the hostname chat.freenode.net, which load balances connections by using round-robin DNS.
**3. Is the linked list an ADT?**
Yes, a linked list is an Abstract Data type i.e ADT.


