Last Updated on November 9, 2022 by Sumit Kumar

A linked list is one of the most famous data structure asked in most coding interviews and have different variety of questions based on different concepts.
In this article, we will learn how to add two numbers represented by linked lists or add two linked lists.
Adding Two Numbers Represented by Linked Lists
Given two positive numbers represented as singly-linked lists containing the digits of the numbers in reverse order. Write a function to return the sum of these two numbers as a linked list.
Problem Statement Understanding for adding two numbers in linked list:
Let’s understand this problem to add two linked lists with help of examples.
Let us consider the 2 linked lists as l1 and l2 shown below to add two linked list:
If
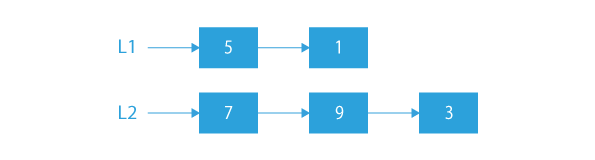
Since it is given that the linked list contains digits of number in reverse order. So, the above two linked lists represent the numbers 15 and 397. So, the resultant linked list should represent the sum of the above two linked lists, i.e., 15+397 = 412. The resultant linked list will also contain the sum in form of a linked list in reverse order.

If
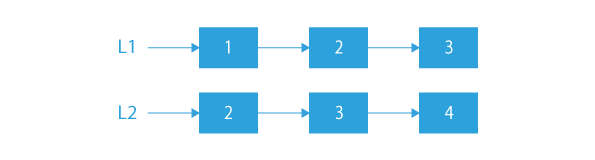
So in this case, the two linked lists represent the numbers 321 and 432. So, the resultant linked list should represent the sum of the above two linked lists, i.e., 321+432 = 753. The resultant linked list will also contain the sum in form of a linked list in reverse order.

I hope you have understood what we have to do in for adding two numbers represented by linked lists. Try to think of an approach to solve it.
Now, let us look at how to approach to add two numbers in linked list.
Approach for adding two numbers in linked lists(Converting the two linked lists to integers)
To add two numbers in the linked list, the simplest thing we can do is to reverse the two linked lists (as they contain the digits in reverse order). Then convert the two numbers in linked lists into integers. Add these integers and convert the sum back to a linked list such that it contains digits in reverse order.
Here, we will need to implement the following functions for adding two numbers represented by linked list:
1) To reverse a linked list.
2) To convert linked list to integers.
3) To convert an integer to a linked list.
Algorithm to add two linked lists
- Reverse the given linked lists l1 and l2.
- Convert the numbers represented by the two linked lists into integers num1 and num2.
- Add the two numbers as sum = num1+num2.
- Convert the above-calculated sum back to a linked list using our to_linkedlist() function which will one-by-one take the digits from the end of the number passed and create a linked list using them. And finally, return it.
ans = to_linkedlist(sum). - Return the resultant linked list ‘ans’ containing the sum.
Since our to_linkedlist() function is taking the digits from the end of the number passed to it and create a linked list by adding new nodes at the end, the resulting linked list will contain the digits of the number in reverse order.
So, our ‘ans’ will contain the sum as a linked list containing digits of sum in reverse order. This is what we required.
Now that you have understood how we are going to add two linked lists, before moving to the implementation try to implement it yourself for adding two numbers in linked list.
Dry Run to add two numbers represented by linked lists
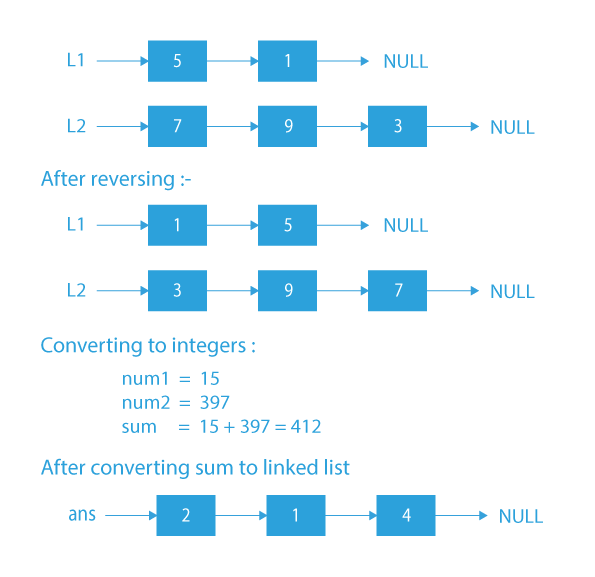
Code Implementation to Add 2 Numbers Represented by Linked Lists
#includeusing namespace std; struct Node { int val; Node* next; Node(int value){ val = value; next = NULL; } }; void push_front(Node** head, int new_val){ Node* new_node = new Node(new_val); new_node->next = *head; *head = new_node; } void printList(Node* head){ Node* i = head; while(i){ cout< val<<" "; i = i->next; } cout<<"\n"; } // function to reverse a linked list Node* reverse_it(Node* head){ Node *prev = NULL; Node *curr = head, *next; while(curr!=NULL){ next = curr->next; curr->next = prev; prev = curr; curr = next; } return prev; } // function to convert a linked list to integer int to_integer(Node* head){ int num = 0; Node* curr = head; while(curr){ int digit = curr->val; num = num*10 + digit; curr = curr->next; } return num; } // function to convert a number to a linked list // containing digits in reverse order Node* to_linkedlist(int x){ Node* head = new Node(0); if(x==0) return head; Node* curr = head; while(x){ int d = x%10; x /= 10; curr->next = new Node(d); curr = curr->next; } return head->next; } // function to add 2 numbers given as linked lists Node* add_list(Node* l1, Node* l2){ // reversing the 2 linked lists l1 = reverse_it(l1); l2 = reverse_it(l2); // converting them into integers int num1 = to_integer(l1); int num2 = to_integer(l2); int sum = num1 + num2; // converting the sum back to // a linked list Node* ans = to_linkedlist(sum); return ans; } int main(){ Node* l1 = NULL; push_front(&l1, 1); push_front(&l1, 5); Node* l2 = NULL; push_front(&l2, 3); push_front(&l2, 9); push_front(&l2, 7); // l1-> 5 1 // l2-> 7 9 3 Node* sum = add_list(l1,l2); printList(sum); // 2 1 4 }
class LinkedList {
Node head1, head2;
static class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
/* Adds contents of two linked lists and prints it */
void addTwoLists(Node first, Node second) {
Node start1 = new Node(0);
start1.next = first;
Node start2 = new Node(0);
start2.next = second;
addPrecedingZeros(start1, start2);
Node result = new Node(0);
if (sumTwoNodes(start1.next, start2.next, result) == 1) {
Node node = new Node(1);
node.next = result.next;
result.next = node;
}
Node res=reverse_it(result.next);
printList(res);
}
static Node reverse_it(Node head)
{
Node prev=null;
Node curr=head,next=null;
while(curr!=null)
{
next=curr.next;
curr.next=prev;
prev=curr;
curr=next;
}
return prev;
}
/* Adds lists and returns the carry */
private int sumTwoNodes(Node first, Node second, Node result) {
if (first == null) {
return 0;
}
int number = first.data + second.data + sumTwoNodes(first.next, second.next, result);
Node node = new Node(number % 10);
node.next = result.next;
result.next = node;
return number / 10;
}
/* Appends preceding zeros in case a list is having lesser nodes than the other one*/
private void addPrecedingZeros(Node start1, Node start2) {
Node next1 = start1.next;
Node next2 = start2.next;
while (next1 != null && next2 != null) {
next1 = next1.next;
next2 = next2.next;
}
if (next1 == null && next2 != null) {
while (next2 != null) {
Node node = new Node(0);
node.next = start1.next;
start1.next = node;
next2 = next2.next;
}
} else if (next2 == null && next1 != null) {
while (next1 != null) {
Node node = new Node(0);
node.next = start2.next;
start2.next = node;
next1 = next1.next;
}
}
}
/* Utility function to print a linked list */
void printList(Node head) {
while (head != null) {
System.out.print(head.data + " ");
head = head.next;
}
System.out.println("");
}
// Driver Code
public static void main(String[] args) {
LinkedList list = new LinkedList();
// creating first list
list.head1 = new Node(1);
list.head1.next = new Node(5);
// creating second list
list.head2 = new Node(3);
list.head2.next = new Node(9);
list.head2.next.next = new Node(7);
System.out.print("Resultant List is ");
// add the two lists and see the result
list.addTwoLists(list.head1, list.head2);
}
}
class Node: def __init__(self, data): self.data = data self.next = None class LinkedList: def __init__(self): self.head = None def push(self, new_data): new_node = Node(new_data) new_node.next = self.head self.head = new_node def addTwoLists(self, first, second): prev = None temp = None carry = 0 while(first is not None or second is not None): fdata = 0 if first is None else first.data sdata = 0 if second is None else second.data Sum = carry + fdata + sdata carry = 1 if Sum >= 10 else 0 Sum = Sum if Sum < 10 else Sum % 10 temp = Node(Sum) if self.head is None: self.head = temp else: prev.next = temp prev = temp if first is not None: first = first.next if second is not None: second = second.next if carry > 0: temp.next = Node(carry) def printList(self): temp = self.head while(temp): print (temp.data,end=' ') temp = temp.next first = LinkedList() second = LinkedList() first.push(1) first.push(5) second.push(3) second.push(9) second.push(7) res = LinkedList() res.addTwoLists(first.head, second.head) res.printList()
Output
2 1 4
Time Complexity: O(n+m), where n,m are the number of nodes in the linked lists
Space Complexity: O(max(n,m)), as the number of digits in sum will depend on the number having more digits.
This approach would work only for numbers that are small enough to fit into integer datatype. What if the number of digits in a number is huge eg., 30? Then the above approach would fail and we need to improve upon it to add two numbers in linked list .
Approach 2 (Simple iteration with 2 pointers)
To add two numbers in a linked list, we can simply iterate the 2 linked lists and take the sum of the values in nodes along with maintaining a carry. While taking sums add the previous carry to it and add a new node to the result containing the last digit in the sum and update the carry for the next iteration.
Algorithm to add two numbers represented by linked lists
- Use 2 pointers to store the head of each linked list and initialize carry as 0.
- Declare a pointer to the node to store our answer.
- Iterate through both the linked list and add the digits pointed by the pointers (if we have reached the end of one of the linked lists and have no further nodes, consider its value as 0 while taking the sum).
- Add a new node with ((sum+carry)%10) as value to our answer and update carry as (sum + carry)/10.
- Repeat steps 3 and 4 till we reach the end of both the linked lists.
- After traversing both the linked lists, if carry > 0 then add this carry to our answer as a new node.
Dry Run to add two linked lists
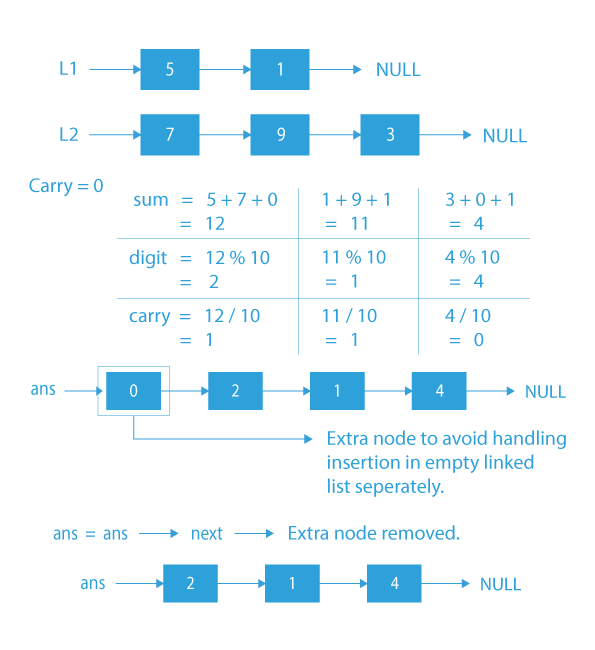
Code Implementation:
#include<bits/stdc++.h>
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
// function to add 2 numbers given as linked lists
Node* add(Node* l1, Node* l2){
Node* ans = new Node(0);
Node* curr = ans;
int carry = 0;
while(l1 || l2){
int sum = 0;
if(l1) sum += l1->val;
if(l2) sum += l2->val;
sum += carry;
curr->next = new Node(sum%10);
curr = curr->next;
carry = sum/10;
if(l1) l1 = l1->next;
if(l2) l2 = l2->next;
}
if(carry){
curr->next = new Node(carry);
}
ans = ans->next;
return ans;
}
int main(){
Node* l1 = NULL;
push_front(&l1, 1);
push_front(&l1, 5);
Node* l2 = NULL;
push_front(&l2, 3);
push_front(&l2, 9);
push_front(&l2, 7);
// l1-> 5 1 = 15
// l2-> 7 9 3 = 397
Node* sum = add(l1,l2);
printList(sum);
// 2 1 4 = 412
}
class Node
{
int val;
Node next;
Node(int value)
{
val = value;
next = null;
}
}
class AddTwoLL
{
static void push_front(Node head, int new_val)
{
Node new_node = new Node(new_val);
new_node.next =head;
head = new_node;
}
static void printList(Node head)
{
Node i = head;
while(i!=null)
{
System.out.print(i.val+" ");
i = i.next;
}
System.out.println();
}
// function to reverse a linked list
static Node reverse_it(Node head)
{
Node prev = null;
Node curr = head, next;
while(curr!=null)
{
next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
// function to convert a linked list to integer
static int to_integer(Node head){
int num = 0;
Node curr = head;
while(curr!=null)
{
int digit = curr.val;
num = num*10 + digit;
curr = curr.next;
}
return num;
}
// function to convert a number to a linked list containing digits in reverse order
static Node to_linkedlist(int x)
{
Node head = new Node(0);
if(x==0) return head;
Node curr = head;
while(x>0)
{
int d = x%10;
x /= 10;
curr.next = new Node(d);
curr = curr.next;
}
return head.next;
}
// function to add 2 numbers given as linked lists
static Node add_list(Node l1, Node l2)
{
// reversing the 2 linked lists
l1 = reverse_it(l1);
l2 = reverse_it(l2);
// converting them into integers
int num1 = to_integer(l1);
int num2 = to_integer(l2);
int sum = num1 + num2;
// converting the sum back to
// a linked list
Node ans = to_linkedlist(sum);
return ans;
}
public static void main(String [] args)
{
Node l1 = null;
push_front(l1, 1);
push_front(l1, 5);
Node l2 = null;
push_front(l2, 3);
push_front(l2, 9);
push_front(l2, 7);
// l1-> 5 1
// l2-> 7 9 3
Node sum = add_list(l1,l2);
printList(sum);
// 2 1 4
}
}
Output
2 1 4
Note that here I have initialized ‘ans’ with a node with value 0 initially. This I did to avoid handling the case of insertion in an empty linked list separately. So, at the end ignored the additional node added and return the list after it.
Space Complexity: O(max(n,m)), as the number of digits in sum will depend on the number having more digits.
To avoid the use of extra space we can store the sum in one of the linked lists itself. Try implementing it yourself.
Conclusion:
In this article, we have seen how to add two numbers represented as linked lists by using two different approaches. We can use any of the approaches to add two numbers in the linked list depending upon the constraints provided.
FAQs
-
In how many different ways we can add two numbers in the linked list?
We can add the two numbers in the linked list by simple iteration with 2 pointers technique, stacks, backtracking, etc. -
How is carry computed for the sum of digits?
Basically, if the sum of digits is less than 10, then carry is 0 else carry is 1. -
What is a Linked list?
The linked list is a set of nodes in which each node has a pointer to the next node and is stored at non-contiguous memory locations.


