Last Updated on November 28, 2022 by Prepbytes

Linked is an important concept of data structures for placement point of view. In an interview, almost all the questions asked related to the linked list. One of the most frequently asked problems “check if linked list is palindrome” is the one from them and top product-based companies like Amazon, Accenture, flipkart, Adobe, and many more.
How to check if linked list is palindrome
We will be given a linked list, and we need to find whether the given list is palindrome or not.
To understand this problem statement, let us take examples.
If the given linked list is 3→1→18→1→3→NULL, and now according to the problem statement, we need to determine whether the given linked list is palindrome or not.
- If we iterate the given list forward and print the elements, we will get: 3,1,18,1,3
- Now, if we iterate the given list backward and print the elements, we will get: 3,1,18,1,3.
- We can see that no matter we iterate forward or backward, we are getting the same output at the end. So, the given list is a palindrome.
At this point, we have understood the problem statement. Now we will try to formulate an approach for this problem.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Let’s move to the approach section.
Approach 1 to check if linked list is palindrome
To check whether a linked list is a palindrome or not, we need to traverse the list backward from the last node of the list, but as our linked list is a singly linked list, we cannot move backwards in the list.
To solve the above problem, we will use a stack and store all the elements of the list in the stack while forward iteration of the list.
- After that, we will again iterate the list and will simultaneously pop an element from the stack at each iteration and will check if this popped element is equal to the current element of the list or not.
- If all the elements are equal, then the list is a palindrome. Else, It is not a palindrome.
Time Complexity to check if linked list is palindrome: O(n), where n is the total number of nodes in the list
Space Complexity to check if linked list is palindrome: O(n), due to the stack
The above approach seems fine, but we are using a stack that is increasing the space complexity. So, we need to think of a better approach where no extra space is used.
Approach 2 to check if linked list is palindrome
Since we cannot move backward in the list, we need to devise an algorithm to get our work done.
We can reverse the second half of the list and then simultaneously compare the elements from the first and second half of the list.
- If all elements of first and the second half are equal, then the list is a palindrome.
- Else, the list is not a palindrome.
Algorithm to check if linked list is palindrome
- If the list is empty or it has only one node then simply return true as an empty list or a list with a single node is always a palindrome.
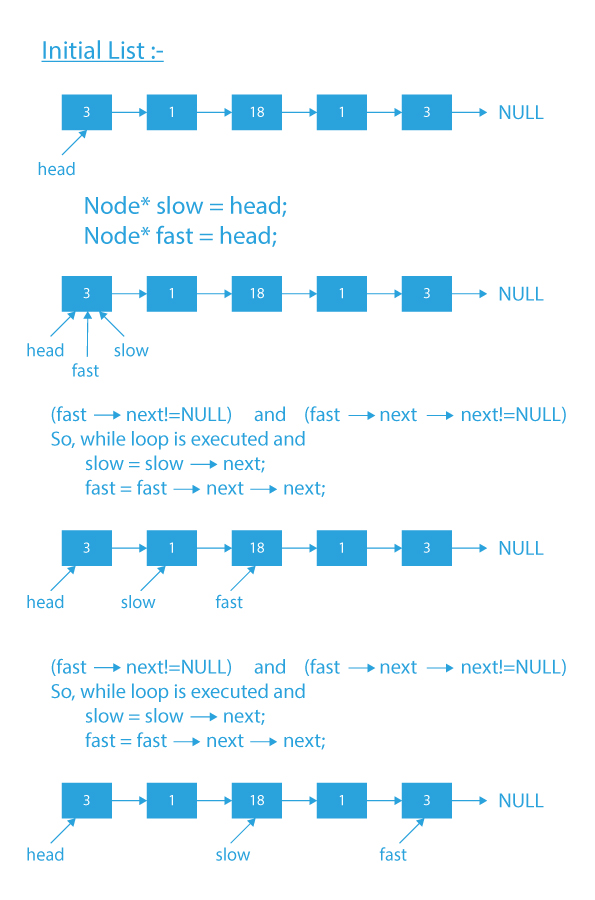
- Initialize two pointers slow and fast with the first node of the list (finding the middle node of the linked list).
- Run a while loop till the fast reach the last or last second node of the list.
- In each iteration, advance slow forward by one node and fast forward by two nodes.
- Now, when the fast is at the end of the list, slow will be pointing to the middle node of the linked list.
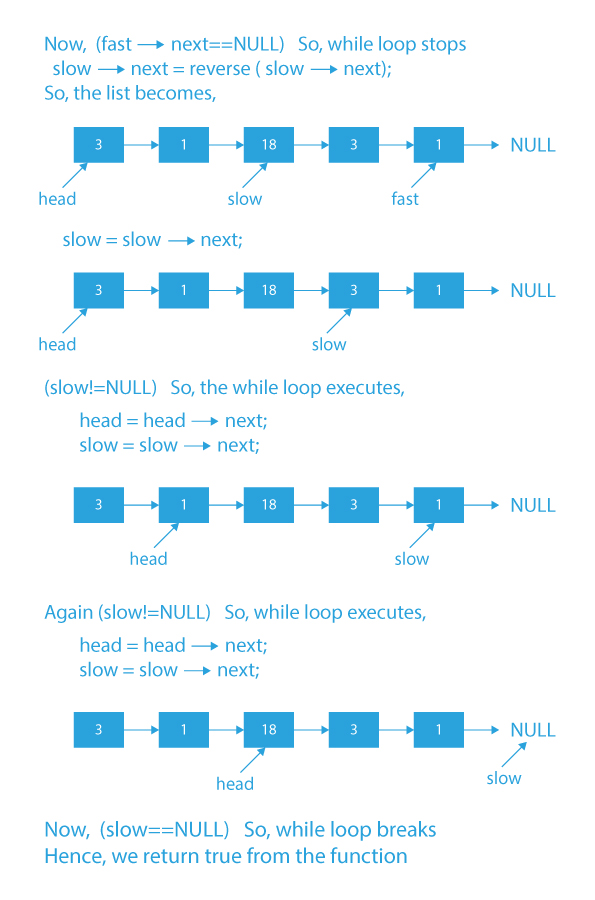
- Now, reverse the second half of the linked list starting from slow->next to the last node of the linked list.
- After that, simultaneously iterate through the first half and the second half of the linked list using pointers head and slow:
- If the data of the node to which head and slow are pointing are not equal, return false.
- Else, advance slow and head by one node.
- After execution of the above while loop, return true from the function.
Dry Run to check if linked list is palindrome
Code Implementation to check if linked list is palindrome
#include <stdio.h>
#include <stdbool.h>
//Represent a node of the singly linked list
struct node{
int data;
struct node *next;
};
//Represent the head and tail of the singly linked list
struct node *head, *tail = NULL;
int size = 0;
//addNode() will add a new node to the list
void addNode(int data) {
//Create a new node
struct node *newNode = (struct node*)malloc(sizeof(struct node));
newNode->data = data;
newNode->next = NULL;
//Checks if the list is empty
if(head == NULL) {
//If list is empty, both head and tail will point to new node
head = newNode;
tail = newNode;
}
else {
//newNode will be added after tail such that tail's next will point to newNode
tail->next = newNode;
//newNode will become new tail of the list
tail = newNode;
}
//Size will count the number of nodes present in the list
size++;
}
//reverseList() will reverse the singly linked list and return the head of the list
struct node* reverseList(struct node *temp){
struct node *current = temp;
struct node *prevNode = NULL, *nextNode = NULL;
//Swap the previous and next nodes of each node to reverse the direction of the list
while(current != NULL){
nextNode = current->next;
current->next = prevNode;
prevNode = current;
current = nextNode;
}
return prevNode;
}
//isPalindrome() will determine whether given list is palindrome or not.
void isPalindrome(){
struct node *current = head;
bool flag = true;
//Store the mid position of the list
int mid = (size%2 == 0)? (size/2) : ((size+1)/2);
//Finds the middle node in given singly linked list
for(int i=1; i<mid; i++){="" current="current-">next;
}
//Reverse the list after middle node to end
struct node *revHead = reverseList(current->next);
//Compare nodes of first half and second half of list
while(head != NULL && revHead != NULL){
if(head->data != revHead->data){
flag = false;
break;
}
head = head->next;
revHead = revHead->next;
}
if(flag)
printf("Given singly linked list is a palindrome\n");
else
printf("Given singly linked list is not a palindrome\n");
}
//display() will display all the nodes present in the list
void display() {
//Node current will point to head
struct node *current = head;
if(head == NULL) {
printf("List is empty\n");
return;
}
printf("Nodes of singly linked list: \n");
while(current != NULL) {
//Prints each node by incrementing pointer
printf("%d ", current->data);
current = current->next;
}
printf("\n");
}
int main()
{
//Add nodes to the list
addNode(1);
addNode(2);
addNode(3);
addNode(2);
addNode(2);
display();
//Checks whether given list is palindrome or not
isPalindrome();
return 0;
}
#include<bits stdc++.h="">
using namespace std;
class Node{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
// This function will reverse the list
Node* reverse(Node *head)
{
Node *prev = NULL, *current = head, *next;
while (current != NULL)
{
next = current->next;
current->next = prev;
prev = current;
current = next;
}
return prev;
}
// This function checks if a list is palindrome
bool isPalindrome(Node* head) {
//check if the list is empty or
//it has a single node
if(head==NULL||head->next==NULL)
return true;
//initialize two pointers
Node* slow=head;
Node* fast=head;
// find the middle node of the list
while(fast->next!=NULL&&fast->next->next!=NULL){
slow=slow->next;
fast=fast->next->next;
}
// reverse the second half of the list
slow->next=reverse(slow->next);
//update the 'slow' pointer
slow=slow->next;
//iterate both the lists simultaneously
while(slow!=NULL){
if(head->data!=slow->data)
return false;
head=head->next;
slow=slow->next;
}
return true;
}
int main(void){
Node* head = NULL;
head = new Node(3);
head->next = new Node(1);
head->next->next = new Node(18);
head->next->next->next = new Node(1);
head->next->next->next->next = new Node(3);
if(isPalindrome(head)){
cout<<"The list is a palindrome";
}else{
cout<<"The list is not a palindrome";
}
return 0;
}
class Node{
int data;
Node next;
Node(int x){
data = x;
}
}
public class Palindrome
{
// This function will reverse the list
static Node reverse(Node head)
{
Node prev =null, current = head, next=null;
while (current != null)
{
next = current.next;
current.next = prev;
prev = current;
current = next;
}
return prev;
}
// This function checks if a list is palindrome
static boolean isPalindrome(Node head)
{
//check if the list is empty or
//it has a single node
if(head==null||head.next==null)
return true;
//initialize two pointers
Node slow=head;
Node fast=head;
// find the middle node of the list
while(fast.next!=null && fast.next.next!=null){
slow=slow.next;
fast=fast.next.next;
}
// reverse the second half of the list
slow.next=reverse(slow.next);
//update the 'slow' pointer
slow=slow.next;
//iterate both the lists simultaneously
while(slow!=null){
if(head.data!=slow.data)
return false;
head=head.next;
slow=slow.next;
}
return true;
}
public static void main(String[] args) {
Node head = null;
head = new Node(3);
head.next = new Node(1);
head.next.next = new Node(18);
head.next.next.next = new Node(1);
head.next.next.next.next = new Node(3);
if(isPalindrome(head)){
System.out.println("List is palindrome");
}else{
System.out.println("List is not palindrome");
}
}
}
class Node:
def __init__(self,data):
self.data = data
self.next = None
# This function will reverse the list
def reverse(head):
prev = None
current = head
while(current is not None):
next = current.next
current.next = prev
prev = current
current = next
head = prev
return head
# This function checks if a list is palindrome
def ispalindrome(head):
# check if the list is empty or it has a single node
if head == None or head.next == None:
return True
# initialize two pointers
slow = head
fast = head
# find the middle node of the list
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
# reverse the second half of the list
slow.next = reverse(slow.next)
# update the 'slow' pointer
slow = slow.next
# iterate both the lists simultaneously
while slow:
if head.data != slow.data:
return False
head = head.next
slow = slow.next
return True
head = None
head = Node(3)
head.next = Node(1)
head.next.next = Node(18)
head.next.next.next = Node(1)
head.next.next.next.next = Node(3)
if ispalindrome(head):
print("The list is a palindrome")
else:
print("The list is not a palindrome")
Output
The list is a palindromeTime Complexity to check if linked list is palindrome: O(n), n is the total number of nodes in the list.
Conclusion
So, in this blog, we have tried to explain how you can check if linked list is palindrome most optimally. If you are new to programming and want to learn more about programming languages, also if you want to solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs related to how to check if linked list is palindrome
1. What is the meaning of palindromic?
A palindrome is a word that reads the same backward and forward. The words, numbers, and sequences which satisfy the palindrome property are called palindromic.
Examples: Words like RADAR, CIVIC, and Numbers like 121, 1331.
2. What is a palindrome number?
Numbers that read the same backward and forward are called palindrome numbers. The numbers 17371, 3, and 121 are palindrome numbers.
3. How do you check if a palindrome is valid in Python?
To check whether the string is a valid palindrome or not using a regular expression you have to make use of re. sub() on a set of alphanumeric characters which needs to be replaced with lowercase characters.


