Last Updated on December 13, 2022 by Prepbytes

This article discusses the most efficient approach to construct a binary tree using a linked list. Constructing binary trees from linked lists will definitely improve your data structures. Having knowledge about data structures like binary trees and linked lists is the most important part if you want to join the IT sector. Let’s discuss our topic “Construct binary tree using linked list” in detail.
How To Make Binary Tree From Linked List
In this question, we are given the level order traversal of a binary tree, in the form of a linked list. We have to construct the complete binary tree from its linked list representation.
Suppose the given linked list is 10 -> 12 -> 13 -> 23 -> 30 -> 36. For each ith node, its children are the (2i+1)th and (2i+2)nd nodes of the list. So, the children of 10 are 12 and 13. The children of 12 are 23 and 30. The children of 13 are 36 and NULL. All other child nodes are NULL. Hence, the complete binary tree is :-
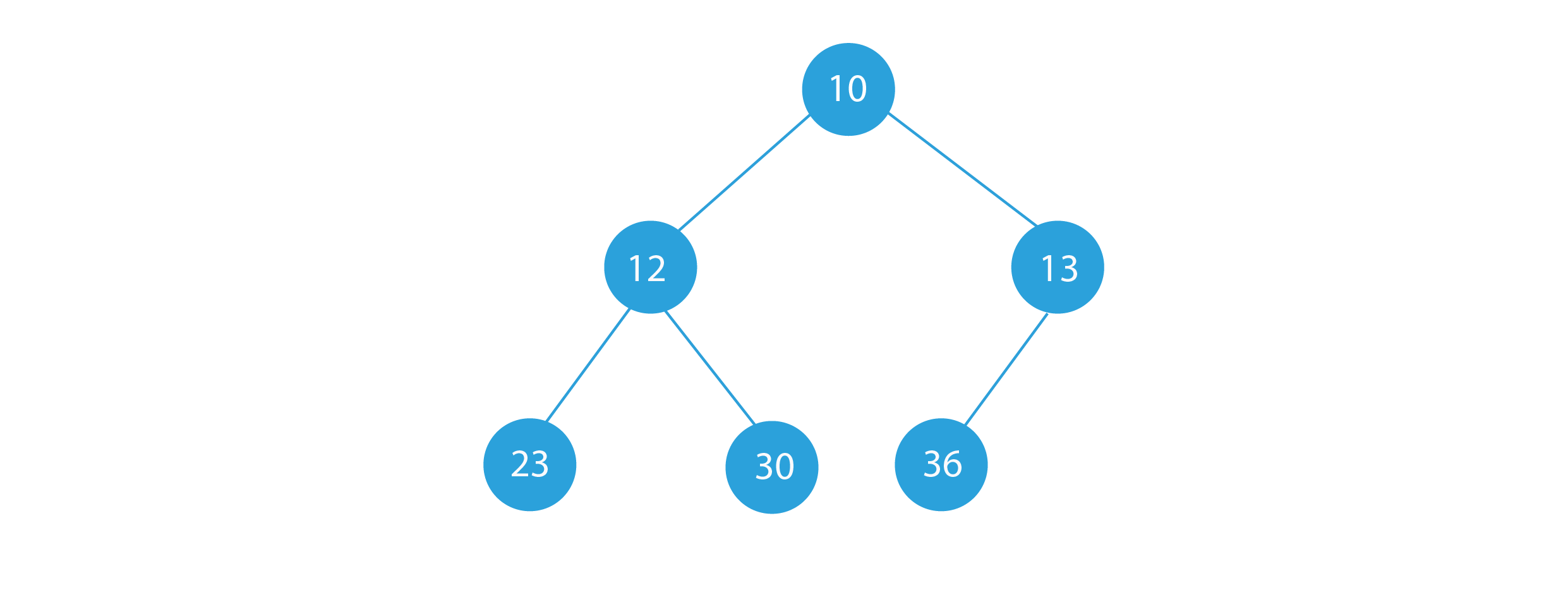
Input:

Output:

Explanation: As we can see, the output has a complete binary tree that has been created from its linked list representation.
This is a very interesting problem. We have to keep in mind that if the index of the root node is x (using 0 based indexing), then its left and right children are stored at the indices 2x+1 and 2x+2. We cannot directly access the nodes, so we have to traverse through the linked list. Let us have a glance at the approach.
Approach To Construct Binary Tree Using Linked List
What will be the root of the binary tree? The head. Yes, the head will be the root of the binary tree, as we are given the level order traversal. As we now know the root of the tree, we also know that the next two nodes of the linked list are the left and right children of the root.
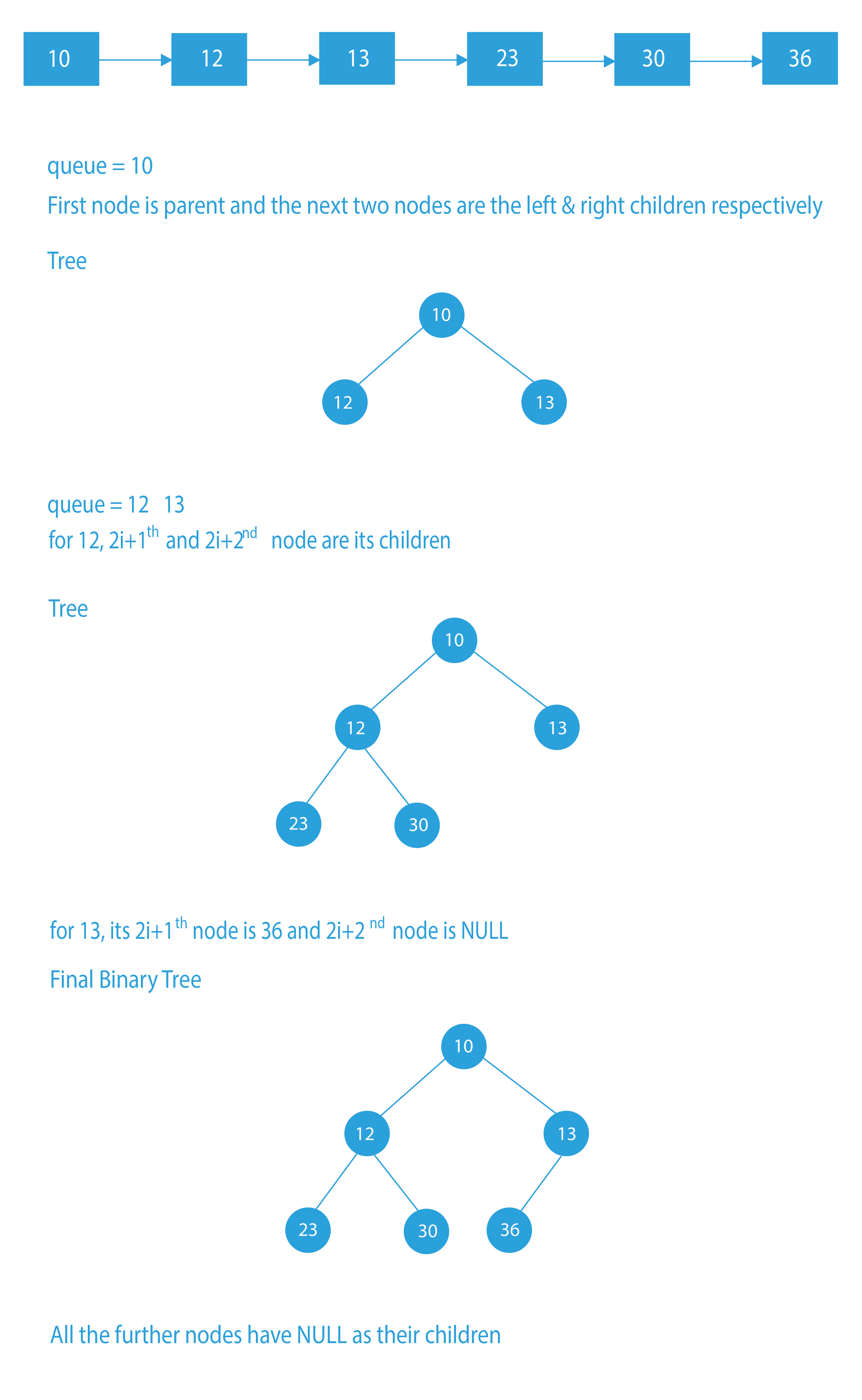
So, now we know the partial binary tree. We are going to do a level order traversal of the binary tree using a queue and traverse the given linked list at the same time.
At every step, we will pick one node from the queue, and make the next two nodes of the linked list the children of the current(parent) node. After this, we are going to enqueue the next two nodes to the queue.
Algorithm To Construct Binary Tree Using Linked List
- Base Case – If the head is NULL, then make the root NULL.
- Create a queue.
- Enqueue the first node of the linked list, and make it the root.
- Traverse through the list, and do the following
- Dequeue a node from the queue. This node is the current parent. Add the next two nodes of the linked list as the children of the current node(parent).
Now, enqueue the two nodes in the queue. - Continue this till the end of the linked list.
Dry Run To Construct Binary Tree Using Linked List
Code Implementation To Construct Binary Tree Using Linked List
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct ListNode
{
int data;
ListNode* next;
};
struct Node
{
int data;
Node *left, *right;
};
void push(struct ListNode** head_ref, int new_data)
{
// allocate node and assign data
struct ListNode* new_node = new ListNode;
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
Node* newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void convertList2Binary(ListNode head, Node &root)
{
queue<node *=""> q;
if (head == NULL)
{
root = NULL;
return;
}
root = newNode(head->data);
q.push(root);
head = head->next;
while (head)
{
Node* parent = q.front();
q.pop();
Node *leftChild = NULL, *rightChild = NULL;
leftChild = newNode(head->data);
q.push(leftChild);
head = head->next;
if (head)
{
rightChild = newNode(head->data);
q.push(rightChild);
head = head->next;
}
parent->left = leftChild;
parent->right = rightChild;
}
}
void inorderTraversal(Node* root)
{
if (root)
{
inorderTraversal( root->left );
cout << root->data << " ";
inorderTraversal( root->right );
}
}
int main()
{
struct ListNode* head = NULL;
push(&head, 36);
push(&head, 30);
push(&head, 23);
push(&head, 13);
push(&head, 12);
push(&head, 10);
Node *root;
convertList2Binary(head, root);
cout << "Inorder Traversal of the constructed Binary Tree is: \n";
inorderTraversal(root);
return 0;
}
import java.util.*;
class ListNode
{
int data;
ListNode next;
ListNode(int d)
{
data = d;
next = null;
}
}
class BinaryTreeNode
{
int data;
BinaryTreeNode left, right = null;
BinaryTreeNode(int data)
{
this.data = data;
left = right = null;
}
}
public class BinaryTree
{
ListNode head;
BinaryTreeNode root;
void push(int new_data)
{
ListNode new_node = new ListNode(new_data);
new_node.next = head;
head = new_node;
}
BinaryTreeNode convertList2Binary(BinaryTreeNode node)
{
Queue<binarytreenode> q =
new LinkedList<binarytreenode>();
if (head == null)
{
node = null;
return null;
}
node = new BinaryTreeNode(head.data);
q.add(node);
head = head.next;
while (head != null)
{
BinaryTreeNode parent = q.peek();
BinaryTreeNode pp = q.poll();
BinaryTreeNode leftChild = null, rightChild = null;
leftChild = new BinaryTreeNode(head.data);
q.add(leftChild);
head = head.next;
if (head != null)
{
rightChild = new BinaryTreeNode(head.data);
q.add(rightChild);
head = head.next;
}
parent.left = leftChild;
parent.right = rightChild;
}
return node;
}
void inorderTraversal(BinaryTreeNode node)
{
if (node != null)
{
inorderTraversal(node.left);
System.out.print(node.data + " ");
inorderTraversal(node.right);
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.push(36);
tree.push(30);
tree.push(23);
tree.push(13);
tree.push(12);
tree.push(10);
BinaryTreeNode node = tree.convertList2Binary(tree.root);
System.out.println("Inorder Traversal of the"+
" constructed Binary Tree is:");
tree.inorderTraversal(node);
}
}
class ListNode:
def __init__(self, data):
self.data = data
self.next = None
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Conversion:
def __init__(self, data = None):
self.head = None
self.root = None
def push(self, new_data):
new_node = ListNode(new_data)
new_node.next = self.head
self.head = new_node
def convertList2Binary(self):
q = []
if self.head is None:
self.root = None
return
self.root = Node(self.head.data)
q.append(self.root)
self.head = self.head.next
while(self.head):
parent = q.pop(0)
leftChild= None
rightChild = None
leftChild = Node(self.head.data)
q.append(leftChild)
self.head = self.head.next
if(self.head):
rightChild = Node(self.head.data)
q.append(rightChild)
self.head = self.head.next
parent.left = leftChild
parent.right = rightChild
def inorderTraversal(self, root):
if(root):
self.inorderTraversal(root.left)
print (root.data,end=" ")
self.inorderTraversal(root.right)
conv = Conversion()
conv.push(36)
conv.push(30)
conv.push(23)
conv.push(13)
conv.push(12)
conv.push(10)
Output
Inorder Traversal of the constructed Binary Tree is
23 12 30 10 36 13Space Complexity To Construct Binary Tree Using Linked List: O(n), the space required to create the binary tree.
This blog discussed in detail about how to construct binary tree using linked list. Data structures like binary trees and linked list always have a huge impact not only in interviews but also in real life. If you want to practice more questions on the linked list, you can follow this link Linked List.
FAQ
1. What are the 4 types of linked list?
There are four key types of linked lists:
- Singly linked lists.
- Doubly linked lists.
- Circular linked lists.
- Circular doubly linked lists.
2. Where is the linked list used?
- Applications of linked lists in computer science: Implementation of stacks and queues.
- Implementation of graphs: Adjacency list representation of graphs is the most popular which uses a linked list to store adjacent vertices.
- Dynamic memory allocation: We use a linked list of free blocks.


