Construct A Doubly Linked List From 2D Matrix

Last Updated on November 27, 2023 by Ankit Kochar

Constructing a doubly linked list from a 2D matrix is a fascinating exercise that involves transforming a two-dimensional data structure into a linked list, specifically a doubly linked list. This process requires traversing through the matrix elements, creating nodes, and linking them in such a way that they form a linked list where each node maintains connections to both its previous and next nodes. Implementing this conversion not only enhances understanding of linked list concepts but also demonstrates the versatility of data structure manipulation. In this article, we will delve into the step-by-step process of constructing a doubly linked list from a 2D matrix, elucidating the methodology and providing a clear, concise implementation guide.

How To Construct 2D Doubly Linked List?

We are provided with a 2D Matrix, and we need to construct a doubly linked list with 4 pointers, namely:

• up
• down
• left
• right

Each node should be connected to its adjacent nodes using these 4 pointers.

Learn programming languages online and consider Example:

Input 2D Matrix:

12 11 10
1 2 3
6 8 9

Output Doubly Linked List:

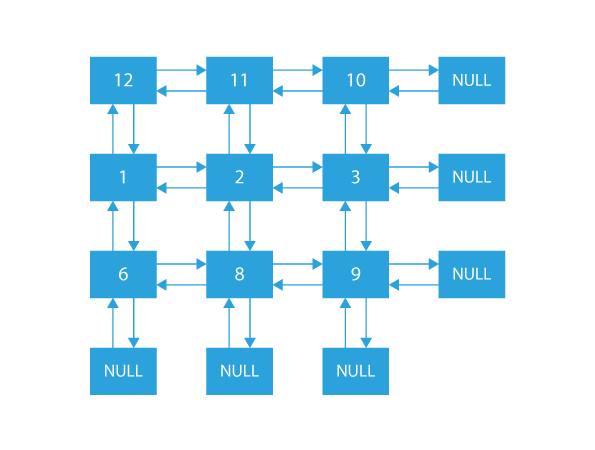
We are given a 2D Matrix with N rows and M columns. Every element at index i, j (i.e., matrix[i][j]) needs to be changed into a node, and it should be linked to all its adjacent cells using 4 pointers given to us.

• up
• left
• right
• down

For example, We are given a Matrix with 3 rows and 3 columns:
12 11 10
1 2 3
6 8 9

• Lets take an example with element matrix[0][0] , i.e 12.

  • It only has 2 adjacent members, matrix[0][1] and matrix[1][0], i.e., 11 and 1 respectively.
  • We need to mark Node 12’s right as 11. Since 11 is right adjacent to 12.
  • We need to mark Node 12’s down as 1. Since 1 is lower adjacent to 12.

• Let’s take another example of the middle element matrix[1][1], i.e. 2

  • It has 4 adjacent, matrix[1][2], matrix[0][1], matrix[2][1], matrix[1][0], which are right, up, down, and left adjacent of element 2.
  • We need to mark Node 2’s right as 3. Since 3 is right adjacent to 2.
  • We need to mark Node 2’s up as 11. Since 11 is the up adjacent to 2.
  • We need to mark Node 2’s down as 8. Since 8 is the lower adjacent to 2.
  • We need to mark Node 2’s left as 1. Since 1 is the left adjacent to 2.

The Structure of Node will be:

struct Node{
    int data;   // To hold the value of the matrix

    // 4 pointers for left, right, up, down for markings.
    Node* left; 
    Node* right;
    Node* up;
    Node* down;

    Node(int x) : data(x), left(NULL), right(NULL), up(NULL), down(NULL) {}
};

Let’s dive into the Approach and Algorithm now.

Approach and Algorithm To Construct 2D Doubly Linked List

The Approach for the given problem statement is straightforward.

• We create a new Node every time we visit an unvisited cell, starting from (0,0).
• We change the left pointer (curr->left) and up pointer (curr->up) of our current node.
• Recur for right pointer (curr->right) and down pointer (curr->down) of our current Node.

Implementation To Construct 2D Doubly Linked List

#include
using namespace std;
struct Node {
    int data;   // To hold the value of the matrix

    // 4 pointers for left, right, up, down for markings.
    Node* left;
    Node* right;
    Node* up;
    Node* down;

    Node(int x) : data(x) , left(NULL) , right(NULL) , up(NULL) , down(NULL) {}
};
Node* constructDoublyLinkedList(int mat[][3], int i, int j, Node* last) {

    //Base Condition
    if (i >= 3 || j >= 3) return NULL;
    // since matrix is of dimension 3x3.

    Node* curr = new Node(mat[i][j]);

    if (j == 0) curr->left = NULL;
    else curr->left = last;

    if (i == 0) curr->up = NULL;
    else curr->up = last;

    //Recursively Calling for right and down pointers

    curr->right = constructDoublyLinkedList(mat, i, j + 1, curr);
    curr->down = constructDoublyLinkedList(mat, i + 1, j, curr);

    return curr;

}
void print(Node* head) {
    // Require 2 pointers, downptr and rightptr, for rows and columns.
    Node* downptr = head;
    Node* rightptr;
    while (downptr) {
        rightptr = downptr;
        while (rightptr) {
            cout << (rightptr->data) << " ";
            rightptr = rightptr->right;
        }
        cout << "\n";
        downptr = downptr->down;
    }
}
int main() {
    int matrix[3][3] = {{12,  11  , 10},
        {1 ,  2  ,  3},
        {6 ,  8  ,  9}
    };

    Node* newList = constructDoublyLinkedList(matrix, 0, 0, NULL);
    print(newList);

    return 0;
}

Output

12 11 10
1 2 3
6 8 9

Time Complexity To Construct 2D Doubly Linked List: O(n*m), where n is the number of rows and m is the number of columns in the given Matrix.
Space Complexity To Construct 2D Doubly Linked List: O(1), constant space complexity, as no extra space is used.

Conclusion
Transforming a 2D matrix into a doubly linked list presents an intriguing problem that highlights the adaptability and versatility of data structures. By systematically traversing the matrix elements and forming nodes linked in a doubly linked list fashion, we bridge the conceptual gap between matrices and linked lists. This process serves as an exercise that strengthens understanding of both data structures and their relationships. The resultant doubly linked list embodies a linear representation of the original matrix, facilitating various operations and manipulations that are inherent to linked lists. Mastery of such transformations not only enriches programming skills but also instills a deeper comprehension of the underlying principles governing data structures.

FAQs Related to Construct a Doubly Linked List From 2D Matrix

Here are FAQs Related to Construct a Doubly Linked List From 2D Matrix.

1. Why construct a doubly linked list from a 2D matrix?
Constructing a doubly linked list from a 2D matrix helps in representing a matrix in a linear fashion, facilitating easy traversal and manipulation. It also serves as a learning exercise to understand the relationships between different data structures.

2. What are the advantages of using a doubly linked list over a matrix?
Doubly linked lists offer flexibility in terms of insertion, deletion, and rearrangement of elements compared to matrices. They occupy memory dynamically, avoiding the need for pre-allocation of fixed space.

3. What challenges might one face in constructing a doubly linked list from a 2D matrix?
Challenges may include managing pointers, keeping track of the matrix indices, and ensuring proper linkage between nodes while traversing the matrix elements.

4. Can this conversion be applied to higher-dimensional arrays or matrices?
Yes, the concept can be extended to higher-dimensional arrays. However, the complexity of traversal and management of pointers increases with the dimensions, making it more intricate.

5. How can I implement this conversion in a programming language?
The implementation involves traversing the matrix, creating nodes for each element, and linking them in a doubly linked list fashion. One can use any preferred programming language and follow a step-by-step algorithm to achieve this conversion.