Last Updated on June 16, 2022 by Ria Pathak

Problem statement
Given two sorted linked lists, derive a linked list that contains the maximum sum path using both the linked lists. The resultant list can contain nodes from both input lists.
When constructing the result list, we may switch to the other input list only at the point of intersection (which means the two nodes with the same value in the two lists).
Try avoiding the use of extra space.
Problem Statement Understanding
To understand the given problem, let’s take an example:
Let us consider 2 sorted linked lists a and b as:
List a =

List b =

We need to construct a maximum sum linked list out of them, and we are allowed to jump between the lists at their points of intersection. At each point of intersection, we have two choices:
- Either we can continue in the same linked list,
- Or we may switch to the other linked list.
We have to make these choices such as to form the linked list with maximum sum.
So for the given linked lists, our maximum sum linked list will be:
resultant maximum sum linked list:

In the resultant maximum sum linked list.
- 1→3 is from list a.
- Switching occurs at 3 to list b.
- 12→42→90 are from list b.
- No switching occurred at point of intersection 90.
- 125→240 is from list b.
- Switching occurs at 240 to list a.
- 517 is from list a.
We switch from a list y to list x only when the sum of consecutive nodes in list x between a pair of nodes in greater than the sum of consecutive nodes in list y between the same pair of nodes.
Explanation
From the above linked list a and b, we can see that:
- Between the common pair (3,90), the sum of nodes in list a = (31) while the sum of nodes in list b = (12+42) = 54. So as we can see that the sum of consecutive nodes in b is greater than that in a, that’s why while forming the maximum sum linked list we switched from list a to list b at point of intersection 3.
I hope from the above example it is clear what we have to do in the problem. So now, before jumping to the approach, try to think how will you approach this problem?
It’s okay if your approach is brute force, we will try to optimize it together.
Let’s have a glance at the approach.
Approach
Now, how do we approach such a problem?
- The idea here is to keep track of the sum between two common nodes, along with pointers to the start and end of the region.
- Compare the sums and select the larger sum region among the two.
- And then make the pointer at the end of our answer region point to the max sum region. Update the answer region.
Now let’s look at a step-by-step algorithm for the above approach.
Algorithm
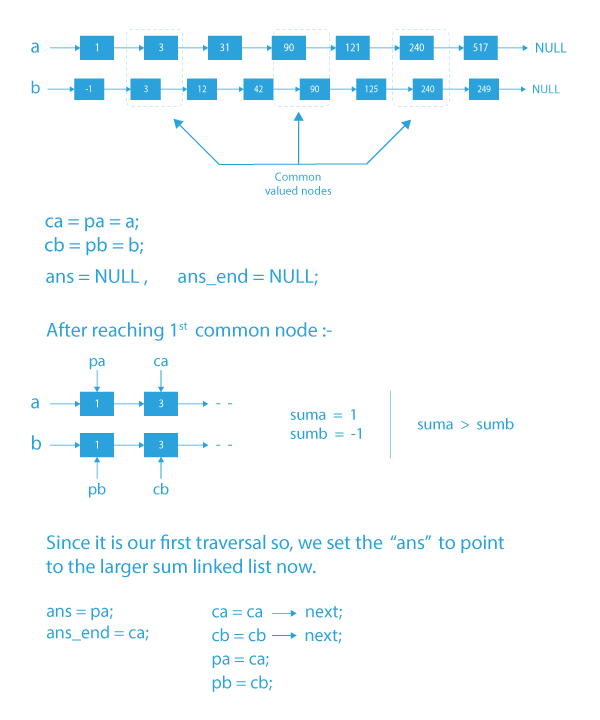
- Initialize pointers to keep track of the current region under consideration in both the linked lists, and also to maintain the start and end of our answer.
pa=ca=NULL (for current region in linked list a)
pb=cb=NULL (for current region in linked list b)
ans=ans_end=NULL - Now iterate in both the linked list, using ca and cb, till the nodes become equal and store the sum of nodes in suma, and sumb.
- Since the linked lists are sorted, we will move forward in the linked list whose current node has a smaller value.
- At the end of each region, compare the two sums.
- For the first iteration, set ans to the larger sum linked list in that iteration and ans_end to the end pointer of that region (either ca or cb depending on the sum).
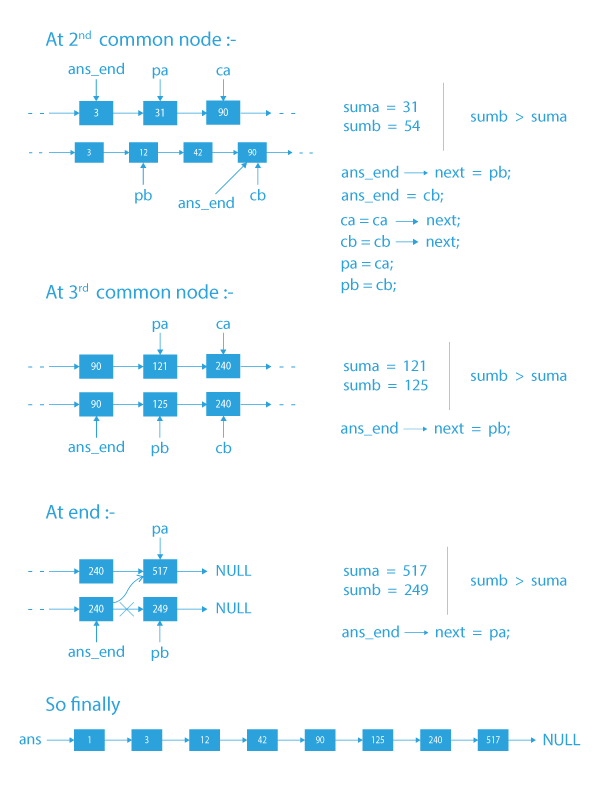
- For the rest of the iterations, set next of ans_end to point to the larger sum region( ans_end->next = pb if sumb>suma else ans_end->next = pa).
- Update ans_end as the end of the selected region (ans_end=cb if sumb>suma else ans_end=ca) and make ca = ca->next and cb=cb->next. Finally make pa = ca and pb = cb to store the beginning of the next region in a and b respectively.
- Repeat steps 2 to 7 until we reach the end of both the linked lists.
- In the end, we will have our maximum sum linked list pointed by ans.
This way, our algorithm will find the required maximum sum linked list in O(n+m) time and O(1) space.
Dry Run
Code Implementation
#include#include struct Node { int data; //data belong to that node struct Node *next; //next pointer }; // Push the data to the head of the linked list void push(struct Node **head, int data) { //Allocation memory to the new node struct Node* newnode = (struct Node*)malloc(sizeof(struct Node)); //Assigning data to the new node newnode->data = data; //Adjusting next pointer of the new node newnode->next = *head; //New node becomes the head of the list *head = newnode; } // Method that adjusts the pointers and prints the final list void finalMaxSumList(struct Node *a,struct Node *b) { struct Node *result = NULL; // Assigning pre and cur to the head of the // linked list. struct Node *pre1 = a; struct Node *curr1 = a; struct Node *pre2 = b; struct Node *curr2 = b; // Till either of the current pointers is not // NULL execute the loop while (curr1 != NULL || curr2 != NULL) { // Keeping 2 local variables at the start of every // loop run to keep track of the sum between pre // and cur pointer elements. int sum1 = 0, sum2 = 0; // Calculating sum by traversing the nodes of linked // list as the merging of two linked list. The loop // stops at a common node while (curr1!=NULL && curr2!=NULL && curr1->data!=curr2->data) { if (curr1->data < curr2->data) { sum1 += curr1->data; curr1 = curr1->next; } else // (curr2->data < curr1->data) { sum2 += curr2->data; curr2 = curr2->next; } } // If either of current pointers becomes NULL // carry on the sum calculation for other one. if (curr1 == NULL) { while (curr2 != NULL) { sum2 += curr2->data; curr2 = curr2->next; } } if (curr2 == NULL) { while (curr1 != NULL) { sum1 += curr1->data; curr1 = curr1->next; } } // First time adjustment of resultant head based on // the maximum sum. if (pre1 == a && pre2 == b) result = (sum1 > sum2)? pre1 : pre2; // If pre1 and pre2 don't contain the head pointers of // lists adjust the next pointers of previous pointers. else { if (sum1 > sum2) pre2->next = pre1->next; else pre1->next = pre2->next; } // Adjusting previous pointers pre1 = curr1, pre2 = curr2; // If curr1 is not NULL move to the next. if (curr1) curr1 = curr1->next; // If curr2 is not NULL move to the next. if (curr2) curr2 = curr2->next; } // Print the resultant list. while (result != NULL) { printf("%d ", result->data); result = result->next; } } //Main driver program int main() { //Linked List 1 : 1->3->30->90->110->120->NULL //Linked List 2 : 0->3->12->32->90->100->120->130->NULL struct Node *head1 = NULL, *head2 = NULL; push(&head1, 120); push(&head1, 110); push(&head1, 90); push(&head1, 30); push(&head1, 3); push(&head1, 1); push(&head2, 130); push(&head2, 120); push(&head2, 100); push(&head2, 90); push(&head2, 32); push(&head2, 12); push(&head2, 3); push(&head2, 0); finalMaxSumList(head1, head2); return 0; }
#includeusing namespace std; struct Node{ int val; Node *next; Node(int x){ val = x; next = NULL;} }; void push_front(Node **head, int x){ Node* temp = new Node(x); temp->next = *head; *head = temp; } void printit(Node *head){ cout<<"head -> "; while(head){ cout< val<<" -> "; head = head->next; } cout<<"NULL \n"; } Node* maxsumlist(Node* a, Node* b){ Node *ca, *cb; Node *pa, *pb; ca = pa = a; cb = pb = b; Node *ans = NULL, *ans_end = NULL; while(ca!=NULL || cb!=NULL){ int suma = 0, sumb = 0; // to calculate sums between two common nodes in // the two linked lists while(ca!=NULL && cb!=NULL && ca->val!=cb->val){ if(ca->val < cb->val){ suma += ca->val; ca = ca->next; } else { sumb += cb->val; cb = cb->next; } } if(ca==NULL || cb==NULL){ while(ca){ suma += ca->val; ca = ca->next; } while(cb){ sumb += cb->val; cb = cb->next; } } // if it is our first traversal if( pa == a || pb == b){ if(suma > sumb){ ans = pa; ans_end = ca; } else { ans = pb; ans_end = cb; } } else { if(suma > sumb){ ans_end->next = pa; ans_end = ca; } else { ans_end->next = pb; ans_end = cb; } } if(ca) ca = ca->next; if(cb) cb = cb->next; pa = ca; pb = cb; } return ans; } int main() { Node *a, *b; a = b = NULL; push_front(&a,517); push_front(&a,240); push_front(&a,121); push_front(&a,90); push_front(&a,31); push_front(&a,3); push_front(&a,1); push_front(&b,249); push_front(&b,240); push_front(&b,125); push_front(&b,90); push_front(&b,42); push_front(&b,12); push_front(&b,3); push_front(&b,-1); Node* ans = maxsumlist(a,b); printit(ans); }
class MaxSum
{
Node head;
class Node
{
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
// Method to adjust pointers and print final list
void MaxSumList(Node a, Node b)
{
Node result = null;
Node pre1 = a, curr1 = a;
Node pre2 = b, curr2 = b;
while (curr1 != null || curr2 != null)
{
int sum1 = 0, sum2 = 0;
// to calculate sums between two common nodes in
// the two linked lists
while (curr1 != null && curr2 != null &&
curr1.data != curr2.data)
{
if (curr1.data sum2) ? pre1 : pre2;
else
{
if (sum1 > sum2)
pre2.next = pre1.next;
else
pre1.next = pre2.next;
}
pre1 = curr1;
pre2 = curr2;
if (curr1 != null)
curr1 = curr1.next;
if (curr2 != null)
curr2 = curr2.next;
}
while (result != null)
{
System.out.print(result.data + " ");
result = result.next;
}
System.out.println();
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
/* Driver code */
public static void main(String args[])
{
MaxSum llist1 = new MaxSum();
MaxSum llist2 = new MaxSum();
llist1.push(517);
llist1.push(240);
llist1.push(121);
llist1.push(90);
llist1.push(31);
llist1.push(3);
llist1.push(1);
llist2.push(249);
llist2.push(240);
llist2.push(125);
llist2.push(90);
llist2.push(42);
llist2.push(12);
llist2.push(3);
llist2.push(-1);
llist1.MaxSumList(llist1.head, llist2.head);
}
}
Output
1 3 12 42 90 125 240 517
Time Complexity: O(n+m), since we are traversing both the linked lists once.
[forminator_quiz id=”4098″]
Here n and m are the total numbers of nodes in the given linked lists.
So, in this article, we have understood how to construct a Maximum Sum Linked List out of two Sorted Linked Lists. This is an important question when it comes to coding interviews. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.


