Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Linked list articles

Delete the middle of a Linked List

Aman Sharma

Last Updated on June 9, 2022 by Ria Pathak

Introduction

The linked list is one of the most important data structures to learn while preparing for interviews. Having a good grasp of Linked Lists can be a huge plus point in a coding interview.

Problem Statement

In this problem, we are given a singly linked list. We have to delete the middle node of the given list.

Problem Statement Understanding

Let’s try to understand the problem statement with an example.

The middle node of this list is 6. We have to remove the middle node from the list. After we remove the middle node, the final linked list will look like this:

Now,

The middle node of this list is 6. We have to remove the middle node from the list. After we remove the middle node, the final linked list will look like this:

This question is not a very complex one. We can easily think of a Brute force solution, in which we find the length of the linked list, store it in an integer N and then delete the (N/2)th node from the list, with the help of a simple deletion process.

Let us have a glance at the above approach.

Approach and Algorithm (Brute Force)

The approach is going to be pretty simple.

  • Firstly, we will count the number of nodes in the given list and store it in a variable N.
  • Then we will find the position of the middle node, which will be equal to mid = (N/2).
  • Now we will traverse the list from head while(mid– >1).
  • When the above condition of while(mid– > 1) violates, we will delete the middle node by performing following operation currrentNode → next = currentNode → next → next.

In this way, the link gets successfully changed, and the middle nodes gets deleted.

Time Complexity – O(N), as no nested traversal is needed.
Space Complexity – O(1), as only temporary variables are being created.

Can we solve this question without actually finding the length of the linked list?

Yes. We can use the slow and fast pointer method to find the middle of the given linked list. This method is the most efficient when it comes to finding the middle of a linked list. The slow and fast method is explained in detail in the next approach.

Approach (Slow and Fast pointer method)

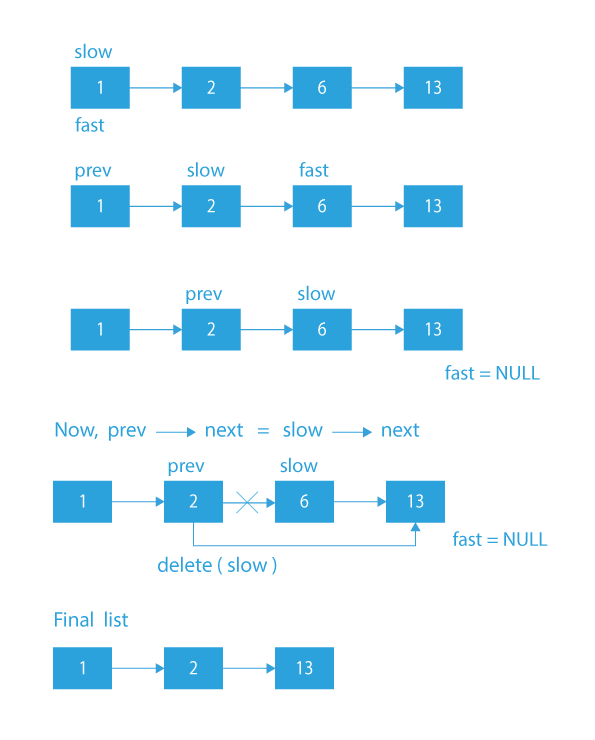
The approach is going to use the two pointers method. We are going to create two pointers, say slow and fast. Both the pointers will point to the head initially. Now, the slow pointer will take one step, while the fast pointer will take two steps. When the fast pointer will reach the node, the slow pointer will be pointing to the middle node. In every iteration, we will also store the slow pointer in a temp variable before incrementing it.

So, we now have the node just before the middle node. We will simply change the links now.

Algorithm

  • Base case 1 – If the head is NULL, return NULL.
  • Base case 2 – If the head is the only node in the list, delete the head and return NULL.
  • Create the slow and fast pointer, both will be initiated at the head.
  • Make the fast pointer take two steps and the slow pointer 1 step. In every iteration, before incrementing the slow pointer, we will store it in a temp variable.
  • When the fast pointer reaches the end, the slow pointer will be pointing to the middle node, and the temp will be pointing to the (middle-1)th node.
  • Now, to change the links – make the temp point to the next of the slow pointer.
  • In the end, delete the slow pointer and return NULL.

Dry Run

Code Implementation

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int data;
    struct Node* next;
};
 
// Deletes middle node and returns
// head of the modified list
struct Node* deleteMid(struct Node* head)
{
    // Base cases
    if (head == NULL)
        return NULL;
    if (head->next == NULL) {
        free(head);
        return NULL;
    }
 
    // Initialize slow and fast pointers
    // to reach middle of linked list
    struct Node* slow_ptr = head;
    struct Node* fast_ptr = head;
 
    // Find the middle and previous of middle.
// To store previous of slow_ptr   
struct Node* prev;
    while (fast_ptr != NULL
&& fast_ptr->next != NULL) {
        fast_ptr = fast_ptr->next->next;
        prev = slow_ptr;
        slow_ptr = slow_ptr->next;
    }
 
    // Delete the middle node
    prev->next = slow_ptr->next;
    free(slow_ptr);
 
    return head;
}
 
// A utility function to print
// a given linked list
void printList(struct Node* ptr)
{
    while (ptr != NULL) {
        printf("%d->",ptr->data);
        ptr = ptr->next;
    }
    printf("NULL\n");
}
 
// Utility function to create a new node.
struct Node* newNode(int x)
{
    struct Node* node = malloc(sizeof(struct Node*));
    node->data = x;
    node->next = NULL;
    return node;
}
 
/* Driver program to test above function*/
int main()
{
    /* Start with the empty list */
    struct Node* head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(6);
    head->next->next->next = newNode(13);
 
    printf("Given Linked List\n");
    printList(head);
 
    head = deleteMid(head);
 
    printf("Linked List after deletion of middle\n");
    printList(head);
 
    return 0;
}

#include <bits stdc++.h="">
using namespace std;

struct Node {
    int data;
    struct Node* next;
};

struct Node* deleteMid(struct Node* head)
{
    
    if (head == NULL)
        return NULL;
    if (head->next == NULL) {
        delete head;
        return NULL;
    }

    struct Node* slow_pointer = head;
    struct Node* fast_pointer = head;

struct Node* prev;
    while (fast_pointer != NULL
&& fast_pointer->next != NULL) {
        fast_pointer = fast_pointer->next->next;
        prev = slow_pointer;
        slow_pointer = slow_pointer->next;
    }

    prev->next = slow_pointer->next;
    delete slow_pointer;
 
    return head;
}

void printList(struct Node* ptr)
{
    while (ptr != NULL) {
        cout << ptr->data << "->";
        ptr = ptr->next;
    }
    cout << "NULL\n";
}

Node* newNode(int data)
{
    struct Node* temp = new Node;
    temp->data = data;
    temp->next = NULL;
    return temp;
}

int main()
{

    struct Node* head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(6);
    head->next->next->next = newNode(13);
 
    cout << "Given Linked List\n";
    printList(head);
 
    head = deleteMid(head);
 
    cout << "Linked List after deletion of middle\n";
    printList(head);
 
    return 0;
}


public class PrepBytes {


    static class Node {
        int data;
        Node next;
    }

    static Node deleteMid(Node head)
    {

        if (head == null)
            return null;
        if (head.next == null) {
            return null;
        }

        Node slow_ptr = head;
        Node fast_ptr = head;

        Node prev = null;

        while (fast_ptr != null
&& fast_ptr.next != null) {
            fast_ptr = fast_ptr.next.next;
            prev = slow_ptr;
            slow_ptr = slow_ptr.next;
        }

        prev.next = slow_ptr.next;

        return head;
    }

    static void printList(Node ptr)
    {
        while (ptr != null) {
            System.out.print(ptr.data + "->");
            ptr = ptr.next;
        }
        System.out.println("NULL");
    }

    static Node newNode(int data)
    {
        Node temp = new Node();
        temp.data = data;
        temp.next = null;
        return temp;
    }


    public static void main(String[] args)
    {

        Node head = newNode(1);
        head.next = newNode(2);
        head.next.next = newNode(6);
        head.next.next.next = newNode(13);

        System.out.println("Given Linked List");
        printList(head);

        head = deleteMid(head);

        System.out.println("Linked List after deletion of middle");
        printList(head);
    }
}

class Node:
	
	def __init__(self, data):
		
		self.data = data
		self.next = None

class LinkedList:
	
	def __init__(self):

		self.head = None

	def addToList(self, data):
		
		newNode = Node(data)
		if self.head is None:
			self.head = newNode
			return
			
		last = self.head
		
		while last.next:
			last = last.next
			
		last.next = newNode

	def __str__(self):
		
		linkedListStr = ""
		temp = self.head
		
		while temp:
			linkedListStr += str(temp.data) + "->"
			temp = temp.next
			
		return linkedListStr + "NULL"

	def deleteMid(self):

		if (self.head is None or
			self.head.next is None):
			return

		slow_Ptr = self.head
		fast_Ptr = self.head

		prev = None

		while (fast_Ptr is not None and
			fast_Ptr.next is not None):
			fast_Ptr = fast_Ptr.next.next
			prev = slow_Ptr
			slow_Ptr = slow_Ptr.next

		prev.next = slow_Ptr.next

linkedList = LinkedList()
linkedList.addToList(1)
linkedList.addToList(2)
linkedList.addToList(6)
linkedList.addToList(13)

print("Given Linked List")
print(linkedList)

linkedList.deleteMid()

print("Linked List after deletion of middle")
print(linkedList)

Output

Given Linked List
1→2→6→13→NULL
Linked List after deletion of middle
1→2→13→NULL

Time Complexity: O(n), as list traversal is needed.
[forminator_quiz id=”3877″]

So, in this article, we have tried to explain the most efficient approach to delete the middle of a linked list. This is an important problem when it comes to coding interviews. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.

Leave a Reply

Your email address will not be published. Required fields are marked *

Close

Related Post