Last Updated on March 10, 2022 by Ria Pathak

Problem Statement
Given two singly linked lists, which may or may not intersect each other. Write a function to return the intersection point of the two linked lists. If they don’t intersect, return NULL.
Problem Statement Understanding
What do we mean by the intersection of two linked lists?
By intersection, we mean that the two linked lists merge into one linked list at some node. This means they will have some nodes common from the end.
Example:
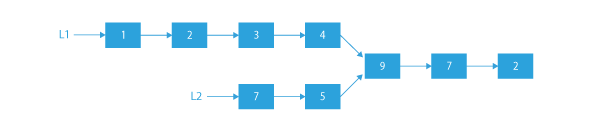
The above 2 linked lists intersect at the node having value 9.
In this problem, we have to find this intersection point of the two given linked list.
Now that we have understood what we have to do, think of how we can approach this problem?
Approach 1 (Using hash-set)
One thing we can do is to traverse one of the linked lists and for each node check if it is present in the other linked list. And we return the first matching node as our intersection point.
Now, how to check for the presence of a node in the linked list?
One approach would be that to check for each node of one of the linked lists, we traverse through the other one completely.
But this method would take a lot of time. So, can we do better to check the presence of a node?
We can use a hash-set to store all nodes of the first linked list and check if any node of the second linked list is there or not. By doing so, we reduce the total time taken with the expense of extra space.
Now that you have an idea of what we are going to do, before moving ahead, try to implement it yourself.
Algorithm
- Declare a hash-set.
- Insert all the nodes of one of the linked lists into the hash-set.
- Now, traverse the other linked list, and for each node check if it is present in the hash-set or not.
- If the node is present, then that is the required intersection point.
- If no node of the second linked list is found in the hash-set, then the two linked lists do not intersect.
Code Implementation
#include#include /* Link list node */ struct Node { int data; struct Node* next; }; int getCount(struct Node* head); int _getIntesectionNode(int d, struct Node* head1, struct Node* head2); int getIntesectionNode(struct Node* head1, struct Node* head2) { int c1 = getCount(head1); int c2 = getCount(head2); int d; if (c1 > c2) { d = c1 - c2; return _getIntesectionNode(d, head1, head2); } else { d = c2 - c1; return _getIntesectionNode(d, head2, head1); } } int _getIntesectionNode(int d, struct Node* head1, struct Node* head2) { int i; struct Node* current1 = head1; struct Node* current2 = head2; for (i = 0; i < d; i++) { if (current1 == NULL) { return -1; } current1 = current1->next; } while (current1 != NULL && current2 != NULL) { if (current1 == current2) return current1->data; current1 = current1->next; current2 = current2->next; } return -1; } int getCount(struct Node* head) { struct Node* current = head; int count = 0; while (current != NULL) { count++; current = current->next; } return count; } int main() { struct Node* newNode; struct Node* head1 = (struct Node*)malloc(sizeof(struct Node)); head1->data = 10; struct Node* head2 = (struct Node*)malloc(sizeof(struct Node)); head2->data = 3; newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = 6; head2->next = newNode; newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = 9; head2->next->next = newNode; newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = 15; head1->next = newNode; head2->next->next->next = newNode; newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = 30; head1->next->next = newNode; head1->next->next->next = NULL; printf("\n The node of intersection is %d \n", getIntesectionNode(head1, head2)); getchar(); }
#include<bits stdc++.h>
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
Node* get_intersection(Node* l1, Node* l2){
unordered_set<node*> list1;
for(Node* i=l1;i!=NULL;i=i->next){
list1.insert(i);
}
for(Node* i=l2;i!=NULL;i=i->next){
if(list1.find(i)!=list1.end()){
// we found the intersection
return i;
}
}
// if no intersection found
return NULL;
}
int main(){
Node* l1 = NULL;
push_front(&l1, 4);
push_front(&l1, 3);
push_front(&l1, 2);
push_front(&l1, 1);
Node* l2 = NULL;
push_front(&l2, 5);
push_front(&l2, 7);
// l1-> 1 2 3 4
// l2-> 7 5
Node* l3 = NULL;
push_front(&l3, 2);
push_front(&l3, 7);
push_front(&l3, 9);
Node *i = l1, *j = l2;
while(i && i->next) i = i->next;
while(j && j->next) j = j->next;
i->next = l3;
j->next = l3;
cout<<"l1: "; printList(l1);
// 1 2 3 4 9 7 2
cout<<"l2: "; printList(l2);
// 7 5 9 7 2
Node *intersection = get_intersection(l1,l2);
if(intersection != NULL){
cout<<"l1 and l2 intersect at : "<<intersection->val;
}
else {
cout<<"l1 and l2 doesn't intersect at eny point";
}
}#include<bits stdc++.h="">
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
Node* get_intersection(Node* l1, Node* l2){
unordered_set<node*> list1;
for(Node* i=l1;i!=NULL;i=i->next){
list1.insert(i);
}
for(Node* i=l2;i!=NULL;i=i->next){
if(list1.find(i)!=list1.end()){
// we found the intersection
return i;
}
}
// if no intersection found
return NULL;
}
int main(){
Node* l1 = NULL;
push_front(&l1, 4);
push_front(&l1, 3);
push_front(&l1, 2);
push_front(&l1, 1);
Node* l2 = NULL;
push_front(&l2, 5);
push_front(&l2, 7);
// l1-> 1 2 3 4
// l2-> 7 5
Node* l3 = NULL;
push_front(&l3, 2);
push_front(&l3, 7);
push_front(&l3, 9);
Node *i = l1, *j = l2;
while(i && i->next) i = i->next;
while(j && j->next) j = j->next;
i->next = l3;
j->next = l3;
cout<<"l1: "; printList(l1);
// 1 2 3 4 9 7 2
cout<<"l2: "; printList(l2);
// 7 5 9 7 2
Node *intersection = get_intersection(l1,l2);
if(intersection != NULL){
cout<<"l1 and l2 intersect at : "<<intersection->val;
}
else {
cout<<"l1 and l2 doesn't intersect at eny point";
}
}
import java.util.*;
class Node
{
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
class VisitedI
{
public static void Print(Node n)
{
Node cur = n;
while (cur != null) {
System.out.print(cur.data + " ");
cur = cur.next;
}
System.out.println();
}
// function to find the intersection of two node
public static Node MegeNode(Node n1, Node n2)
{
// define hashset
HashSet hs = new HashSet();
while (n1 != null) {
hs.add(n1);
n1 = n1.next;
}
while (n2 != null) {
if (hs.contains(n2)) {
return n2;
}
n2 = n2.next;
}
return null;
}
public static void main(String[] args)
{
// list 1
Node n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
// list 2
Node n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
System.out.println("List 1 is :");
Print(n1);
System.out.println("List 2 is :");
Print(n2);
System.out.println("After merging :"+MegeNode(n1, n2).data);
}
}
# Python program to get intersection
# point of two linked list
class Node :
def __init__(self, d):
self.data = d
self.next = None
# Function to print the list
def Print(n):
cur = n
while (cur != None) :
print(cur.data, end=" ")
cur = cur.next
print("")
# Function to find the intersection of two node
def get_intersection(n1, n2):
# Define hashset
hs = set()
while (n1 != None):
hs.add(n1)
n1 = n1.next
while (n2 != None):
if (n2 in hs):
return n2
n2 = n2.next
return None
# Driver code
# list 1
n1 = Node(4)
n1.next = Node(3)
n1.next.next = Node(2)
n1.next.next.next = Node(1)
# list 2
n2 = Node(7)
n2.next = Node(5)
n3 = Node(9)
n3.next = Node(7)
n3.next.next = Node(2)
n1.next.next.next.next = n3
n2.next.next = n3
Print(n1)
Print(n2)
print(get_intersection(n1, n2).data)
Output
l1: 1 2 3 4 9 7 2
l2: 7 5 9 7 2
l1 and l2 intersect at : 9
Time Complexity: O(n+m), as in the worst case when there is no intersection point, we need to traverse both linked lists.
Space Complexity: O(n), as we are storing all the nodes of the first linked list in a hash-set.
Where n and m are the numbers of nodes in the first and second linked lists, respectively.
Can we do some improvements?
Approach 2 (By finding the lengths of two linked lists)
Yes, we can do some improvements if we know the lengths of the linked lists. Let’s understand this with an example:
Example
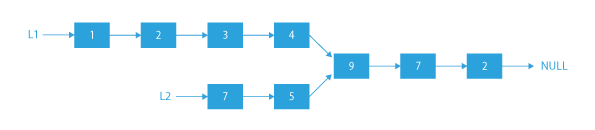
1) Let n and m be the lengths of the 2 linked lists (n = 7, m = 5).
2) Let d be the difference in their lengths (d = 2).
3) Let us look at the distance of the intersection of two linked lists from the beginning. For l1 it is 5 and for l2 it is 3.
4) Now if we move d=2 steps in the larger linked list then we will be at the same distance from the intersection point. Now, if we move together in both the lists, we will meet at the intersection point.
In this approach, we don’t use any extra space.
Now that you have an idea of what we are going to do, before moving ahead, try to implement it yourself.
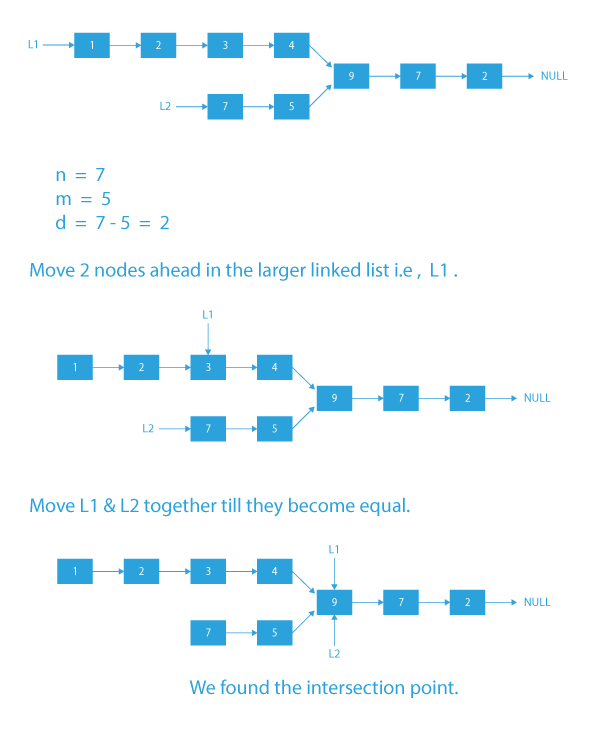
Algorithm
- Find the lengths of the two linked lists n and m.
- Find their absolute difference d.
- Traverse d steps ahead in the larger linked list.
- Now traverse both the linked lists together till their nodes become equal.
- Nodes will become equal only if they are the same node or they both are NULL.
- Once they become equal, we can return the equal node as our intersection point.
Dry Run
Code Implementation
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
struct Node {
int data;
struct Node* next;
};
int getCount(struct Node* head);
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2);
int getIntesectionNode(struct Node* head1, struct Node* head2)
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2)
{
int i;
struct Node* current1 = head1;
struct Node* current2 = head2;
for (i = 0; i < d; i++) {
if (current1 == NULL) {
return -1;
}
current1 = current1->next;
}
while (current1 != NULL && current2 != NULL) {
if (current1 == current2)
return current1->data;
current1 = current1->next;
current2 = current2->next;
}
return -1;
}
int getCount(struct Node* head)
{
struct Node* current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->next;
}
return count;
}
int main()
{
struct Node* newNode;
struct Node* head1 = (struct Node*)malloc(sizeof(struct Node));
head1->data = 10;
struct Node* head2 = (struct Node*)malloc(sizeof(struct Node));
head2->data = 3;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 6;
head2->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 9;
head2->next->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
printf("\n The node of intersection is %d \n",
getIntesectionNode(head1, head2));
getchar();
}
#include<bits stdc++.h="">
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
void printList(Node* head){
Node* i = head;
while(i){
cout<<i->val<<" ";
i = i->next;
}
cout<<"\n";
}
int get_length(Node* head){
int len = 0;
while(head!=NULL){
head = head->next;
len++;
}
return len;
}
Node* get_intersection(Node* l1, Node* l2){
int n = get_length(l1);
int m = get_length(l2);
int d = abs(n-m);
// moving d steps ahead in larger linked list
if(n>m){
while(d--) l1 = l1->next;
} else {
while(d--) l2 = l2->next;
}
// now l1 will become equal to l2
// only if they intersect or
// when they both become NULL
while(l1!=l2){
l1 = l1->next;
l2 = l2->next;
}
return l1;
}
int main(){
Node* l1 = NULL;
push_front(&l1, 4);
push_front(&l1, 3);
push_front(&l1, 2);
push_front(&l1, 1);
Node* l2 = NULL;
push_front(&l2, 5);
push_front(&l2, 7);
// l1-> 1 2 3 4
// l2-> 7 5
Node* l3 = NULL;
push_front(&l3, 2);
push_front(&l3, 7);
push_front(&l3, 9);
Node *i = l1, *j = l2;
while(i && i->next) i = i->next;
while(j && j->next) j = j->next;
i->next = l3;
j->next = l3;
cout<<"l1: "; printList(l1);
// 1 2 3 4 9 7 2
cout<<"l2: "; printList(l2);
// 7 5 9 7 2
Node *intersection = get_intersection(l1,l2);
if(intersection != NULL){
cout<<"l1 and l2 intersect at : "<<intersection->val;
}
else {
cout<<"l1 and l2 doesn't intersect at eny point";
}
}
class VisitedII {
Node head1, head2;
static class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
/*function to get the intersection point of two linked
lists head1 and head2 */
int getNode()
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
/* function to get the intersection point of two linked
lists head1 and head2 where head1 has d more nodes than
head2 */
int _getIntesectionNode(int d, Node node1, Node node2)
{
int i;
Node current1 = node1;
Node current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
/*Takes head pointer of the linked list and
returns the count of nodes in the list */
int getCount(Node node)
{
Node current = node;
int count = 0;
while (current != null) {
count++;
current = current.next;
}
return count;
}
public static void main(String[] args)
{
VisitedII list = new VisitedII();
// creating first linked list
list.head1 = new Node(1);
list.head1.next = new Node(2);
list.head1.next.next = new Node(3);
list.head1.next.next.next = new Node(4);
list.head1.next.next.next.next = new Node(5);
// creating second linked list
list.head2 = new Node(10);
list.head2.next = new Node(15);
list.head2.next.next = new Node(30);
if(list.getNode()!=-1)
{
System.out.println("The intersection of both list is :"+list.getNode());
}
else
{
System.out.println("No intersection is possible");
}
}
}
class Node :
def __init__(self, d):
self.data = d
self.next = None
def Print(n):
cur = n
while (cur != None) :
print(cur.data, end=" ")
cur = cur.next
print("")
def get_length(head):
len = 0
while head:
head = head.next
len += 1
return len
def get_intersection(l1, l2):
n = get_length(l1)
m = get_length(l2)
d = abs(n - m)
if n>m:
while (d):
l1 = l1.next
d -= 1
else:
while d:
l2 = l2.next
d -= 1
while l1 != l2:
l1 = l1.next
l2 = l2.next
return l1
n1 = Node(4)
n1.next = Node(3)
n1.next.next = Node(2)
n1.next.next.next = Node(1)
n2 = Node(7)
n2.next = Node(5)
n3 = Node(9)
n3.next = Node(7)
n3.next.next = Node(2)
n1.next.next.next.next = n3
n2.next.next = n3
Print(n1)
Print(n2)
print(get_intersection(n1, n2).data)
Time Complexity: O(n+m), as we need to traverse both linked lists to find their lengths.
[forminator_quiz id=”3872″]
In this blog, we have seen how to find the intersection point of two linked lists by two different methods. Problems like these are good for strengthening your concepts in LinkedList. I would highly recommend you to practice more such problems from Linked List.


