Last Updated on November 28, 2022 by Prepbytes

This article will discuss in detail how to find a triplet from three linked lists with a sum equal to a given number. Linked list is a dominating topic when we look at the data structures and having a good grip on linked list will help in clearing the interviews for the tech interviews. Let’s get back to our topic and see how to find a triplet from three linked lists with a sum equal to a given number.
How to find a triplet from three linked lists with a sum equal to a given number
We will be given three different linked lists and an integer as input. Now, we need to find whether there is a triplet (one from each list) that sums up to the given integer.
To understand the problem statement, let us take examples.
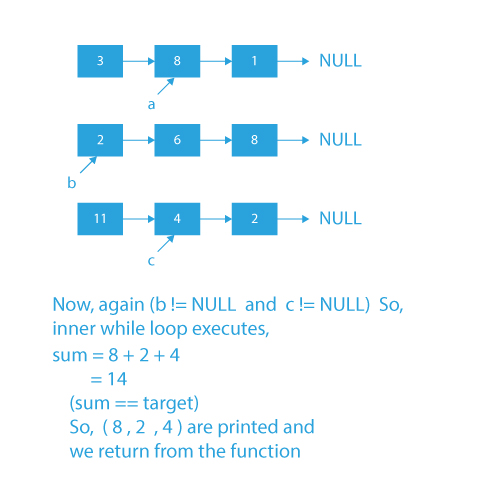
If the linked lists given to us are 3→8→1→5→NULL, 6→2→8→NULL, and 11→4→2→NULL, and the target = 14. Then, according to the problem statement:
- We need to find three Nodes (one from each list) such that they sum up to 14.
- If we select 8 from the first list, 2 from the second list and 4 from the third list, we will get the sum equal to the target=14.
- The required triplet will be (8,2,4).
At this point, we have understood the problem statement. Now we will try to formulate an approach for this problem.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Let’s move to the approach section.
Approach 1
The naive approach that comes to our mind is to first select a node from the first list. Then for each node of the first list, we select a node from the second list, and for each selected node of the second list, we select a node in the third list, and then we check if the sum of the 3 nodes selected is equal to target or not. If the sum is equal to the target, we have our required triplet.
Time Complexity: O(n3) , n is the number of nodes in a list.
The above approach gives the correct result, but its time complexity is high. Can we reduce the time complexity? Let us find out If we can do so in the below approach.
Approach 2
- First, we need to sort the second and third lists (the second list will be sorted in ascending order and the third list in descending order), so that we could be sure whether moving forward or backward in the lists is going to increase or decrease the sum.
- Now, we need to fix a node in the first list and for each node, we need to perform the below steps.
- Calculate the sum of all three-pointers present at different positions on each list.
- If the sum is greater than the target, then we need to decrease the sum, so we need to move forward in the third list (if you visualize carefully, you can see that moving forward in the third list will decrease the sum, because the third list is sorted in descending order).
- Else If the sum is smaller than the target, we need to move forward in the second list to increase our sum (as the second list is sorted in ascending order).
- If the sum is equal, then we can easily print the triplet and show that we have found one triplet in the three given lists.
To see the above approach in more detail, move to the algorithm section.
Algorithm
1) First, sort the second list in ascending order and the third list in descending order.
2) Initialize a pointer a with head of first list.
3) Run a while loop till a is not NULL and inside the loop:
- Initialize pointer b and c with head of second and third list, respectively.
- Run a while loop till b and c are not NULL.
- Initialize variable sum as the sum of values pointed by pointers a,b, and c.
- If the sum is equal to the target, print the values pointed by a,b, and c and return from the function.
- If the sum is less than the target, move forward b by one node. Else, move forward c by one node.
- Move forward a by one node.
Note: For simplicity, in dry run and code implementation, we took second and third linked lists, which are already sorted in ascending and descending order, respectively. If you want to know how to sort a linked list, please feel free to refer to this article for sorting related concepts of linked list. Also, inside the code implementation, we haven’t provided the sorting function (function to sort the linked list); if you want to take unsorted linked lists, please sort them in proper format (the second list will be sorted in ascending order and the third list in descending order) using code from above-mentioned article, before passing them to isSumSorted() function in the code.
Dry Run
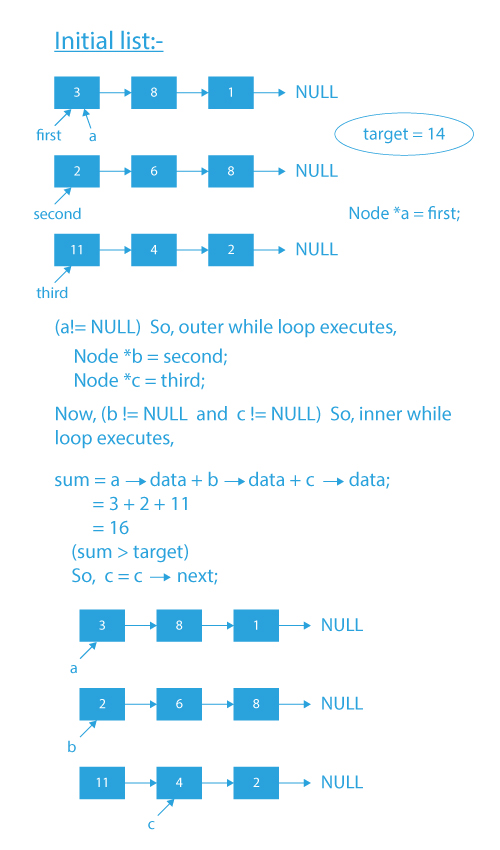
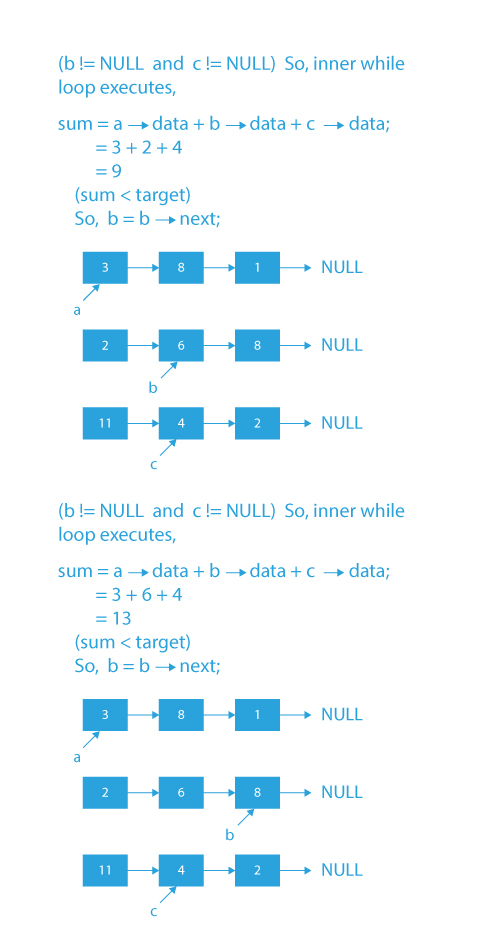
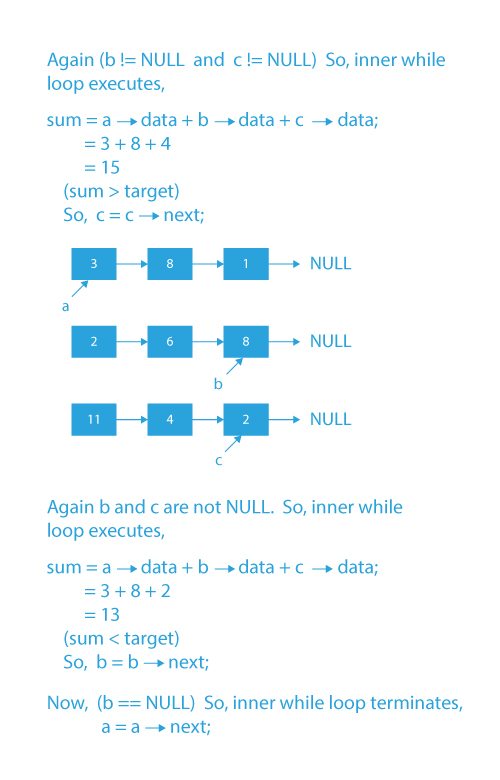
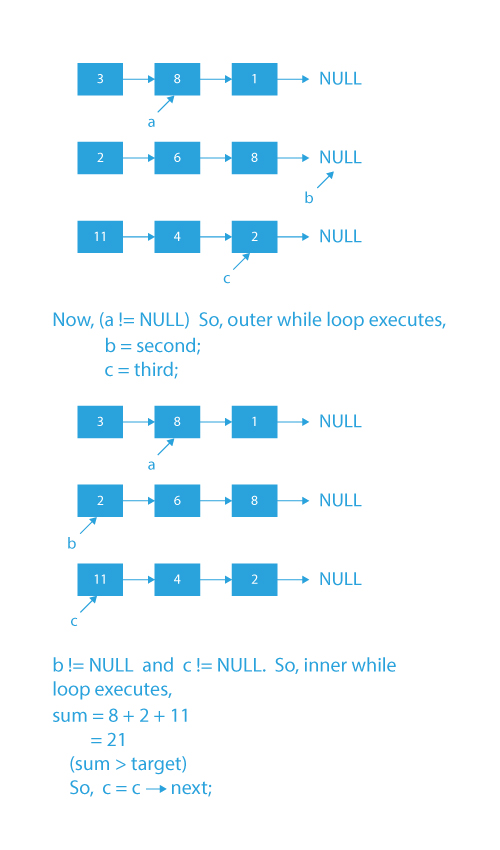
## Code Implementation
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
/* Link list node */
struct Node
{
int data;
struct Node* next;
};
void isSumSorted(struct Node *first,struct Node *second,struct Node *third, int target)
{
struct Node *a = first;
//Select a node in first list and
//traverse the other two lists for
//each selected node
while (a != NULL)
{
struct Node *b = second;
struct Node *c = third;
//select posssible pairs of nodes
//from second and thirs list
//(one from each list)
while (b != NULL && c != NULL)
{
// if sum is equal to our target
int sum = a->data + b->data + c->data;
if (sum == target)
{
printf ("Triplet Found: %d %d %d ", a->data,
b->data, c->data);
return;
}
// If sum is less than target
else if (sum < target)
b = b->next;
else
c = c->next;
}
a = a->next; // Move ahead in list a
}
printf( "No such triplet");
return;
}
struct Node* newNode(int x)
{
struct Node* node = malloc(sizeof(struct Node*));
node->data = x;
node->next = NULL;
return node;
}
int main(void){
struct Node* first = NULL;
first = newNode(3);
first->next = newNode(8);
first->next->next = newNode(1);
struct Node* second = NULL;
second = newNode(2);
second->next = newNode(6);
second->next->next = newNode(8);
struct Node* third = NULL;
third = newNode(11);
third->next = newNode(4);
third->next->next = newNode(2);
isSumSorted(first,second,third,14);
}
#include<bits stdc++.h="">
using namespace std;
class Node{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
void isSumSorted(Node *first, Node *second,Node *third, int target)
{
Node *a = first;
//Select a node in first list and
//traverse the other two lists for
//each selected node
while (a != NULL)
{
Node *b = second;
Node *c = third;
//select posssible pairs of nodes
//from second and thirs list
//(one from each list)
while (b != NULL && c != NULL)
{
// if sum is equal to our target
int sum = a->data + b->data + c->data;
if (sum == target)
{
cout << "Triplet Found: " << a->data << " " <<b->data << " " << c->data;
return;
}
// If sum is less than target
else if (sum < target)
b = b->next;
else
c = c->next;
}
a = a->next; // Move ahead in list a
}
cout << "No such triplet";
return;
}
int main(void){
Node* first = NULL;
first = new Node(3);
first->next = new Node(8);
first->next->next = new Node(1);
Node* second = NULL;
second = new Node(2);
second->next = new Node(6);
second->next->next = new Node(8);
Node* third = NULL;
third = new Node(11);
third->next = new Node(4);
third->next->next = new Node(2);
isSumSorted(first,second,third,14);
}
class Triplet
{
Node head;
class Node
{
int data;
Node next;
Node(int d) {data = d; next = null; }
}
boolean isSumSorted(Triplet llist1, Triplet llist2, Triplet llist3,int givenNumber)
{
Node a = llist1.head;
while (a != null)
{
Node b = llist2.head;
Node c = llist3.head;
// for every node in la pick 2 nodes from lb and lc
while (b != null && c!=null)
{
int sum = a.data + b.data + c.data;
if (sum == givenNumber)
{
System.out.println("Triplet found " + a.data +" " + b.data + " " + c.data);
return true;
}
// If sum is smaller then look for greater value of b
else if (sum < givenNumber)
b = b.next;
else
c = c.next;
}
a = a.next;
}
System.out.println("No Triplet found");
return false;
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
public static void main(String args[])
{
Triplet llist1 = new Triplet();
Triplet llist2 = new Triplet();
Triplet llist3 = new Triplet();
/* Create Linked List llist1 100->15->5->20 */
llist1.push(3);
llist1.push(8);
llist1.push(1);
/*create a sorted linked list 'b' 2->4->9->10 */
llist2.push(2);
llist2.push(6);
llist2.push(8);
/*create another sorted linked list 'c' 8->4->2->1 */
llist3.push(11);
llist3.push(4);
llist3.push(2);
int givenNumber = 14;
llist1.isSumSorted(llist1,llist2,llist3,givenNumber);
}
}
class Node:
def __init__(self, new_data):
self.data = new_data
self.next = None
def push ( head_ref, new_data) :
new_node = Node(0)
new_node.data = new_data
new_node.next = (head_ref)
(head_ref) = new_node
return head_ref
def isSumSorted(headA, headB,headC, givenNumber) :
a = headA
while (a != None) :
b = headB
c = headC
while (b != None and c != None) :
sum = a.data + b.data + c.data
if (sum == givenNumber) :
print("Triplet Found:" , a.data , b.data , c.data)
return True
elif (sum < givenNumber):
b = b.next
else :
c = c.next
a = a.next
print("No such triplet")
return False
headA = None
headB = None
headC = None
headA = push (headA, 20)
headA = push (headA, 4)
headA = push (headA, 15)
headA = push (headA, 10)
headB = push (headB, 10)
headB = push (headB, 9)
headB = push (headB, 4)
headB = push (headB, 2)
headC = push (headC, 1)
headC = push (headC, 2)
headC = push (headC, 4)
headC = push (headC, 8)
givenNumber = 15
isSumSorted (headA, headB, headC, givenNumber)
Output
Triplet Found: 8 2 4
**Time Complexity:** O(n2) ,n is the number of nodes in the list.
This blog had deeply discussed how to find a triplet from three linked lists with a sum equal to a given number. Regularly practicing topics like linked list will increase your potential for getting a good job in tech companies like adobe, google, flipkart, samsung, amazon. For practicing more questions of linked list, our experts have prepared a list of linked list questions, you can check Linked List for it.
## FAQ
**1. What are the 4 types of linked list?**
Types of Linked List – Singly linked, doubly linked and circular
– Singly Linked List.
– Doubly Linked List.
– Circular Linked List.
**2. How do you sum nodes in a linked list?**
So to find the sum of all elements of the singly linked list, we have to navigate to each node of the linked list and add the element’s value to a sum variable. Suppose we have a linked list: 2 -> 27 -> 32 -> 1 -> 5 sum = 2 + 27 + 32 + 1 + 5 = 67.
**3. How can you tell if two linked lists are identical?**
Check if Linked-Lists are identical using linear traversal:
Traverse both the linked lists simultaneously. If the data of the current node for one linked list is not equal to the node of the other one, then return false.
Return true, as both the linked lists are identical.


