C Program For Merge Sort For Linked Lists

Last Updated on July 27, 2023 by Mayank Dham

Introduction

This blog post will guide you through implementing merge sort using linked lists in C. Sorting is a fundamental aspect of data structures. Before delving into the details of merge sort, let’s first grasp the basic concepts involved..

Problem Statement of merge sort using a linked list in C

According to the problem statement, we are given a singly linked list, and we need to sort this singly linked list using merge sort.

What is Merge Sort in C Language

Merge sort is a divide and conquer algorithm.

• It is a recursive algorithm.
• In merge sort, we have to divide the container (container can be an array, list, etc.) into two halves, then we will call merge sort recursively on the two halves.
• These two merge sort calls return a sorted container, and we then merge these sorted containers in such a way that the whole container remains sorted.
• Have a look at the below image to see in a nutshell how merge sort works.

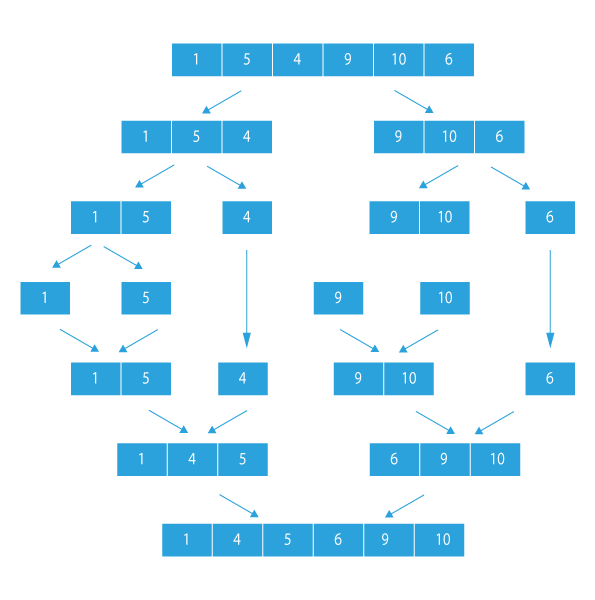
Now, we have a brief understanding of the merge sort algorithm. Let’s learn how to apply merge sort on a singly linked list.

In the case of a linked list, we will recursively divide the list into two sub-lists at each step till the list size is reduced to one and while backtracking from the recursive call, we have two sorted lists, which will be merged together into a single list by merge operation in linear time.

Now we will look at the approach and algorithm, to know how to apply merge sort on a singly linked list.

Approach and Algorithm of merge sort using a linked list in C

1. If the head of the linked list is NULL or (head→ next == NULL), it shows that our linked list is of size 1 or 0 and a linked list of size zero or one is already sorted. So, Don’t do anything, just return head.
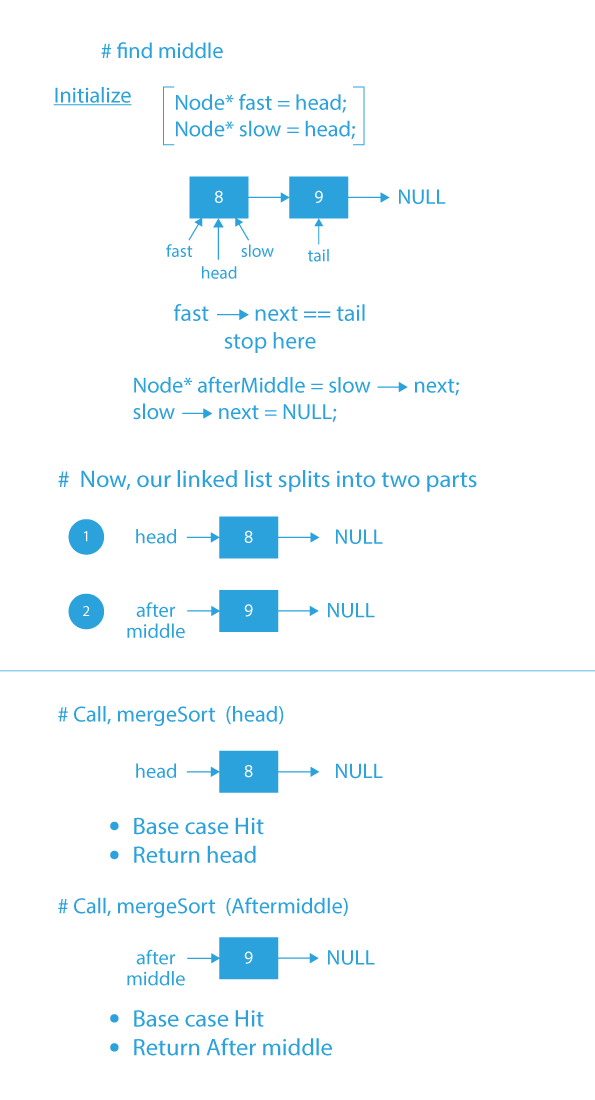
2. If the linked list is of size > 1 then first find the middle of the linked list.
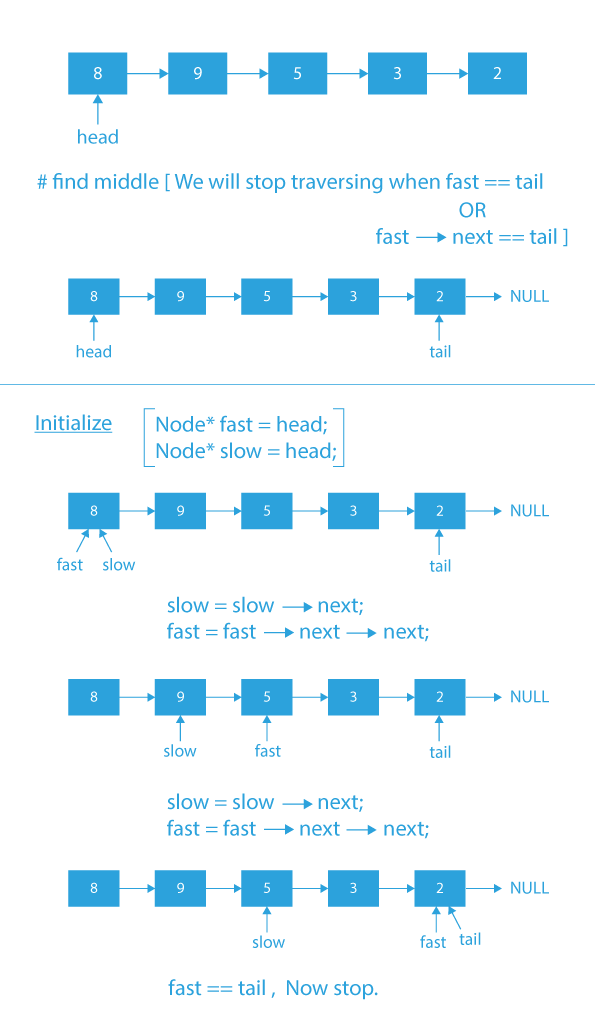
• For finding middle node, use slow and fast pointer method.
• In this method, we take two pointers slow and fast and initialize them with head.
• Then we move the slow pointer by one node and fast pointer by 2 nodes until the fast pointer reaches the tail of the list.
• And when the fast pointer reaches the tail, the slow pointer will be at the middle of the linked list.
• The only reason why slow pointer will be at the middle of the list, when fast reaches tail is because the slow pointer is moving with half the speed of fast pointer and when the fast pointer has traversed the complete list till then the slow pointer will have only traversed half the list, so that’s why slow pointer will be at the middle of the list.
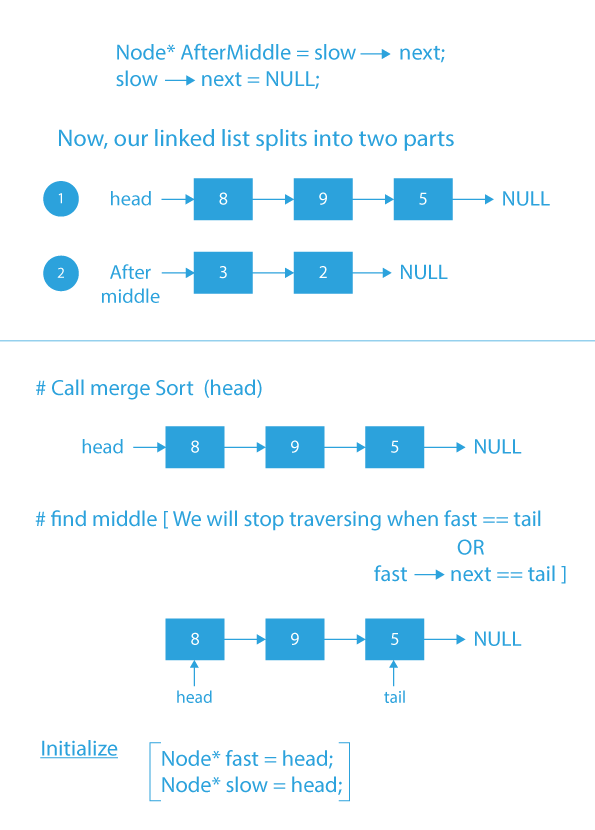
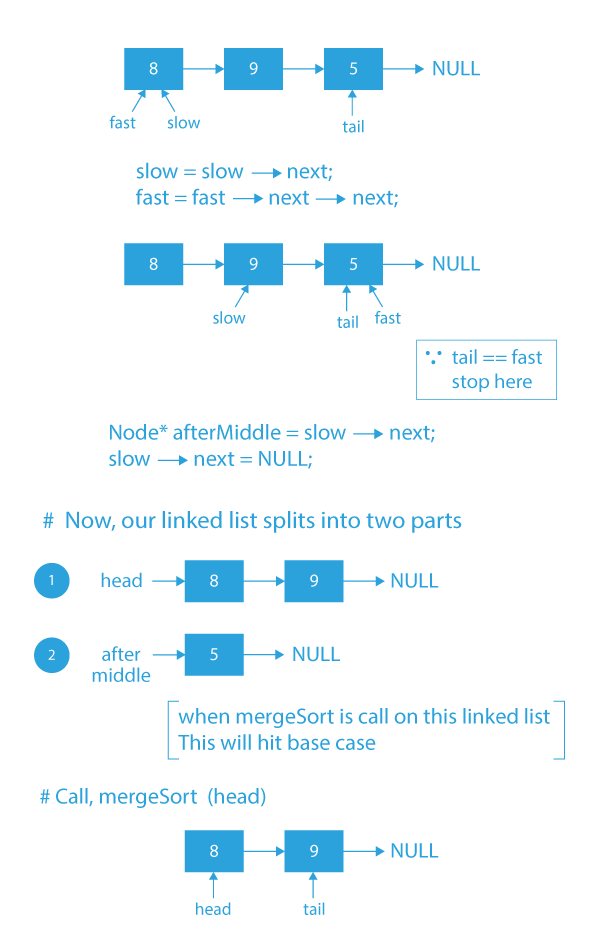
3. Now, store slow → next in a pointer named afterMiddle and assign slow → next = NULL.
4. Recursively call mergeSort() on both left and right sub-linked list and store the new head of the left and right linked list in pointer variable part1 and part2.
5. When the recursive call on the left and right sub-list returns, merge the two linked lists returned by recursive calls (remember that the recursive call will return the sorted lists).
6. Return the final head of the merged linked list.

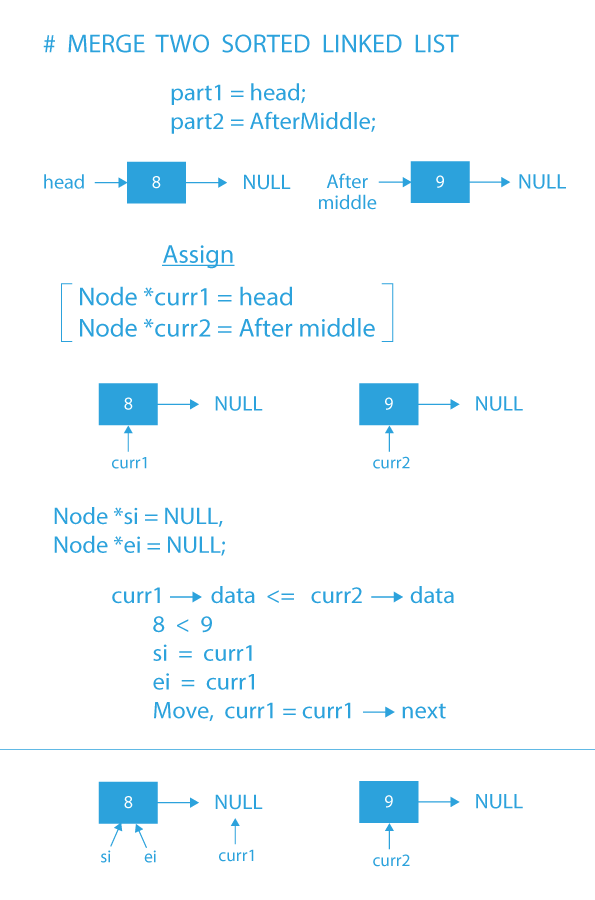
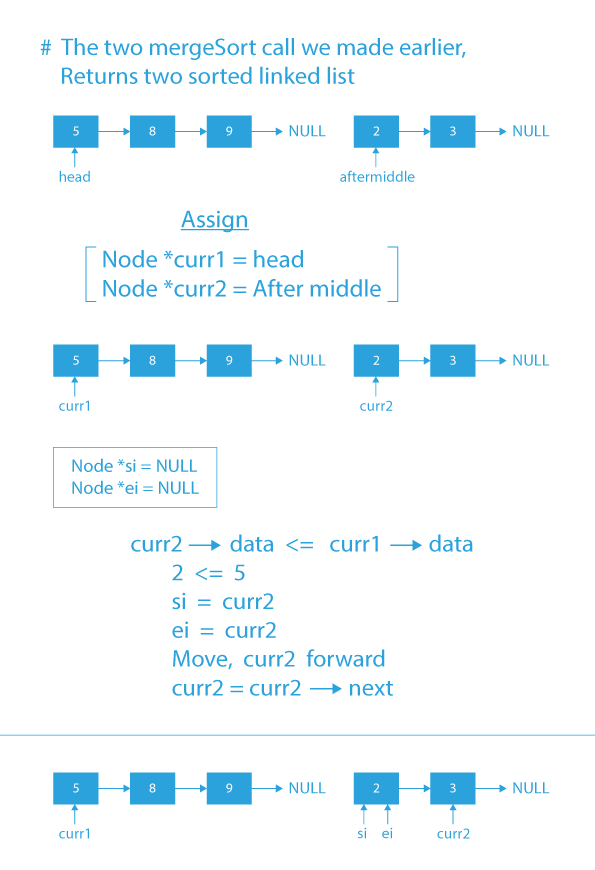
Merging two sorted linked list Algorithm:

When the two recursive calls will return the two sorted lists, then we will merge that sorted list into a single list using these below steps.

1. Initialize two pointer variables named curr1 and curr2 with left sorted sub-list and right sorted sub-list.
2. Initialize two pointer variable named si and ei with NULL; these two pointer variables are the head and tail of the final sorted linked list.
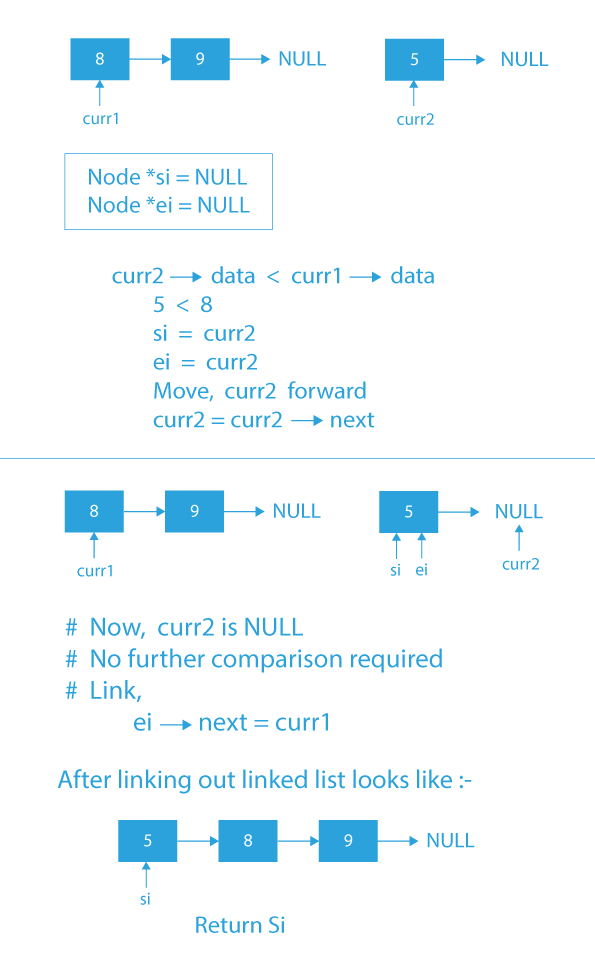
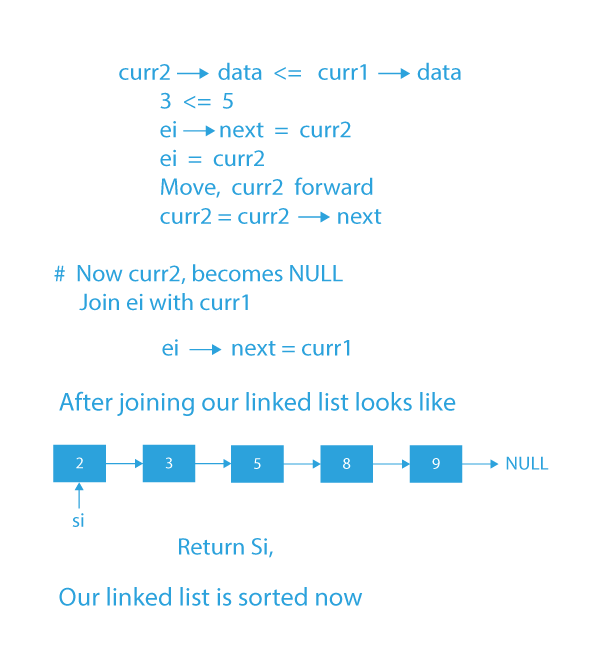
3. If the data of curr1 is less than the data of curr2, then, store curr1 in next of ei & move curr1 to the next of curr1.
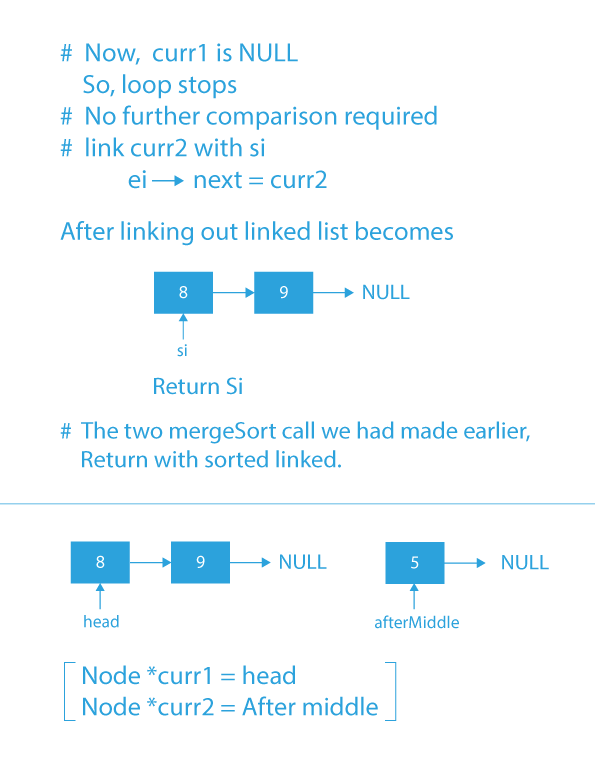
4. Else, if the data of curr2 is less than the data of curr1, then store curr2 in next of ei & move curr2 to the next of curr2.
5. Repeat steps 3 and 4 until either of the curr1 or curr2 is not equal to NULL.
6. Now add any remaining nodes of the first or the second linked list to the merged linked list.
7. Return the head of the merged sorted linked list containing all the nodes of the two sorted sub-lists.

Dry Run of merge sort using a linked list in C

Code Implementation of merge sort using a linked list in C

#include 
#include 

/* Link list node */
struct Node {
    int data;
    struct Node* next;
};

/* function prototypes */
struct Node* SortedMerge(struct Node* a, struct Node* b);
void middle(struct Node* source,
                    struct Node** frontRef, struct Node** backRef);

/* sorts the linked list by changing links */
void MergeSort(struct Node** headRef){
    struct Node* head = *headRef;
    struct Node* a;
    struct Node* b;

    /* Base case -- length 0 or 1 */
    if ((head == NULL) || (head->next == NULL)) {
        return;
    }

    middle(head, &a, &b);

    MergeSort(&a);
    MergeSort(&b);

    *headRef = SortedMerge(a, b);
}

struct Node* SortedMerge(struct Node* a, struct Node* b)
{
    struct Node* result = NULL;

    /* Base cases */
    if (a == NULL)
        return (b);
    else if (b == NULL)
        return (a);

    if (a->data <= b->data) {
        result = a;
        result->next = SortedMerge(a->next, b);
    }
    else {
        result = b;
        result->next = SortedMerge(a, b->next);
    }
    return (result);
}

/* This function splits the list from the middle */
/* After splitting Original list converts into two list 
   first list -> head to the node previous of middle and second list -> middle to end */

void middle(struct Node* source,
                    struct Node** frontRef, struct Node** backRef)
{
    struct Node* fast;
    struct Node* slow;
    slow = source;
    fast = source->next;

    /* Advance 'fast' two nodes, and advance 'slow' one node */
    while (fast != NULL) {
        fast = fast->next;
        if (fast != NULL) {
            slow = slow->next;
            fast = fast->next;
        }
    }

    /* 'slow' is before the midpoint in the list, so split it in two
    at that point. */
    *frontRef = source;
    *backRef = slow->next;
    slow->next = NULL;
}

/* Function to print linked list */
void printList(struct Node* node){
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}

/* Function to insert a node at the beginning of the list */
void push(struct Node** head_ref, int new_data){
    /* allocate node */
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));

    /* assign the data */
    new_node->data = new_data;

    /* link the old list off the new node */
    new_node->next = (*head_ref);

    /* move the head pointer to point to the new node */
    (*head_ref) = new_node;
}

int main(){
    
    struct Node* res = NULL;
    struct Node* a = NULL;

    /* Let's create a new linked lists */
   /* a: 8->9->5->3->2 */
    push(&a, 2);
    push(&a, 3);
    push(&a, 5);
    push(&a, 9);
    push(&a, 8);
    
    printf("Linked List before sorting: \n");
    printList(a);
    printf("\n");
    /* Sort the Linked List */
    MergeSort(&a);
    printf("Linked List after Sorting: \n");
    printList(a);

    getchar();
    return 0;
}

Output

Linked List before sorting
8 9 5 3 2
Linked List after sorting
2 3 5 8 9

Time Complexity of merge sort using a linked list in C: O(n*log n)

So, In this article, we have learned how to apply for the merge sort
program in C. We discussed the merge sort algorithm in detail we also took a look at the time and space complexity of merge sort for linked list in detail. This is an important problem when it comes to coding interviews. If you want to practice more questions on linked lists feel free to solve them at Prepbytes (Linked Lists).

FAQs related to merge sort using linked list in C

Q1. What is merge sort, and how does it work with linked lists in C?
Merge sort is a popular sorting algorithm that employs the divide-and-conquer technique. It works with linked lists by recursively dividing the list into smaller sublists, sorting each sublist individually, and then merging them back together to obtain the sorted output.

Q2. Why is merge sort a preferred sorting algorithm for linked lists?
Merge sort is preferred for linked lists because it has a stable time complexity of O(n log n) and doesn’t require random access, which is advantageous for linked lists where direct access to elements is inefficient.

Q3. What are the time and space complexities of merge sort for linked lists in C?
The time complexity of merge sort for linked lists is O(n log n), where n is the number of elements in the list. The space complexity is O(log n) due to the recursive nature of the algorithm.

Q4. Can merge sort be used for sorting large linked lists efficiently?
Yes, merge sort is efficient for sorting large linked lists due to its O(n log n) time complexity. It divides the sorting process into smaller parts, making it manageable for larger datasets.

Other C Programs
C program to calculate percentage of 5 subjects
C program to convert binary number to decimal number
C program to convert celsius to fahrenheit
C program to convert infix to postfix
C program to find area of circle
C program to find roots of quadratic equation
C program to reverse a number
C program to add two numbers
C program for performing bubble sort on linked list
C program to reverse a linked list