Find modular node in a linked list

Last Updated on November 29, 2022 by Prepbytes

This blog will discuss the best way to solve the famous question “modular node in linked list”. Finding a modular node in linked list will make your linked list topic strong. Having knowledge about data structures like linked list will definitely help in cracking the technical interview of tech giants like Samsung, Amazon, TCS, Wipro, Capgemini, Accenture and Cognizant. Let’s move to our topic to find a modular node in linked list.

How To Find Modular Node In Linked List

In this problem, we have been given a linked list and a positive integer k. Our task is to find the last node whose n%k==0, where n denotes the position of this last node in the linked list.

Let’s try to understand the problem with the help of examples by referring to online programming courses.

Suppose we are given a linked list A → B → C → D → E → F and k = 3.

• According to the problem statement, we have to find the last node of the linked list whose n%k==0, where this n denotes the node’s position in the linked list.

• For the above given linked list, we can see that only for n=3 and n=6 our n%k==0. But as 6>3:

  • So we will have to return the 6^th node of the linked list as our output, as it is the last node of the linked list for which n%k==0.

Output: F

If the linked list is A → B → C → D → E → F → G → H → I and k = 4.

• For the above given linked list, we can see that only for n=4 and n=8 our n%k==0. But as 8>4:

  • So we will have to return the 8^th node of the linked list as our output, as it is the last node of the linked list for which n%k==0.

Output: H

Note: Here in this problem, we are considering 1 based indexing.

Some more examples
Input :

Output : 6

Input :

Output : 9

Now I think from the above examples the problem is clear, and now we have to think about how we can approach it.

Approach To Find Modular Node In Linked List

Our approach will be simple:

• We will traverse the linked list and whenever for any node i%k==0 (i denotes the position of the current node in the linked list) we will update our modular node to be equal to the current node.
• Finally, we will have our modular node at the end of the loop, and now we can return it.

The algorithm for the approach is explained below.

Algorithm To Find Modular Node In Linked List

• We will take a pointer modNode and initialize it with NULL. This pointer will keep track of the last node whose i%k==0.
• Now we will traverse the list and for every i%k==0, we will update our modNode to be equal to the current node.
• Finally, at the end when our list traversal is over, we will return modNode as our output.

Dry Run To Find Modular Node In Linked List

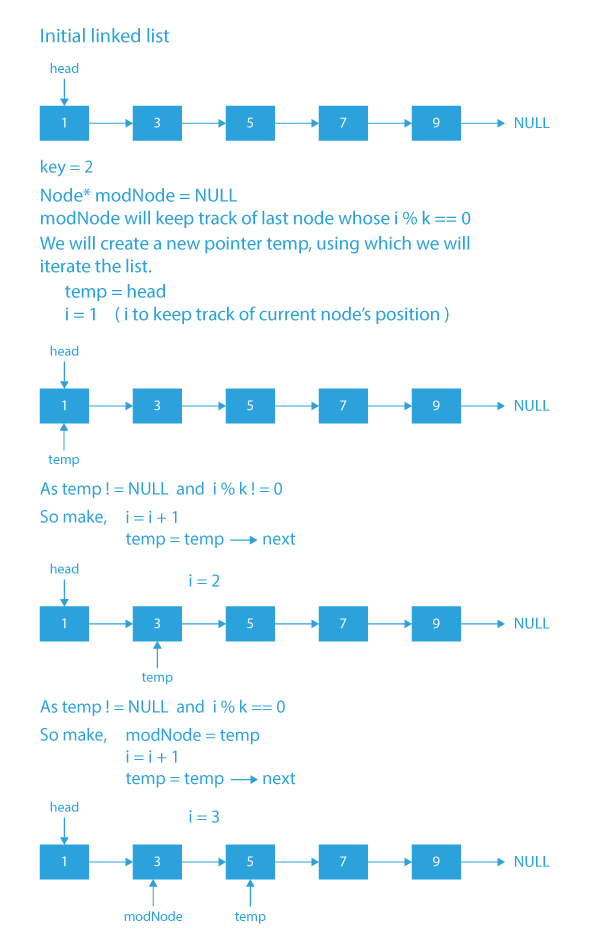
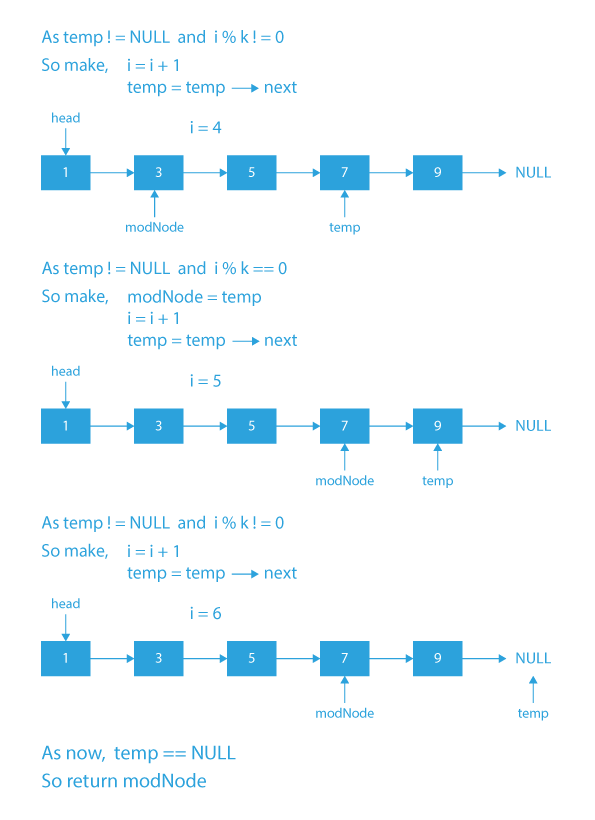
Code Implementation To Find Modular Node In Linked List

#include<stdio.h>
#include<stdlib.h>

struct Node {
    int data;
    struct Node* next;
};
 
/* Function to create a new node with given data */
struct Node* newNode(int data)
{
    struct Node* new_node = malloc(sizeof(struct Node*));
    new_node->data = data;
    new_node->next = NULL;
    return new_node;
}
 
/* Function to find modular node in the linked list */
struct Node* modularNode(struct Node* head, int k)
{
    // Corner cases
    if (k <= 0 || head == NULL)
        return NULL;  
 
    // Traverse the given list
    int i = 1;
    struct Node* modularNode = NULL;
    for (struct Node* temp = head; temp != NULL; temp = temp->next) {
        if (i % k == 0)
            modularNode = temp;
         
        i++;
    }
    return modularNode;
}
 
/* Driver program to test above function */
int main(void)
{
    struct Node* head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->next->next->next = newNode(5);
    int k = 2;
    struct Node* answer = modularNode(head, k);
    printf("\nModular node is ");
    if (answer != NULL)
        printf("%d\n", answer->data);
    else
        printf("null\n");
    return 0;
}

#include <bits stdc++.h="">

struct Node {
    int data;
    Node* next;
};

Node* newNode(int data)
{
    Node* new_node = new Node;
    new_node->data = data;
    new_node->next = NULL;
    return new_node;
}

Node* modularNode(Node* head, int k)
{
    if (k <= 0 || head == NULL)
        return NULL;

    int i = 1;
    Node* modNode = NULL;
    for (Node* temp = head; temp != NULL; temp = temp->next) {
        if (i % k == 0)
            modNode = temp;
        
        i++;
    }
    return modNode;
}

int main()
{
    Node* head = newNode(1);
    head->next = newNode(3);
    head->next->next = newNode(5);
    head->next->next->next = newNode(7);
    head->next->next->next->next = newNode(9);
    int k = 2;
    Node* answer = modularNode(head, k);
    printf("\nModular node is ");
    if (answer != NULL)
        printf("%d\n", answer->data);
    else
        printf("null\n");
    return 0;
}

class Modular
{
    static class Node
    {
        int data;
        Node next;
        Node(int data){
            this.data = data;
        }
    }
    static Node modularNode(Node head, int k)
    {
        if (k <= 0 || head == null)
            return null;
    
        int i = 1;
        Node modularNode = null;
        for (Node temp = head; temp != null; temp = temp.next) {
            if (i % k == 0)
                modularNode = temp;
            
            i++;
        }
        return modularNode;
    }
    public static void main(String[] args)
    {
        Node head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        head.next.next.next = new Node(4);
        head.next.next.next.next = new Node(5);
        int k = 2;
        Node answer = modularNode(head, k);
        System.out.print("Modular node is ");
        if (answer != null)
            System.out.println(answer.data);
        else
            System.out.println("null");
    }
}

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

def newNode(data):
    new_node = Node(data)
    new_node.data = data
    new_node.next = None
    return new_node

def modularNode(head, k):
    
    if (k <= 0 or head == None):
        return None

    i = 1
    modularNode = None
    temp = head
    while (temp != None):
        if (i % k == 0):
            modularNode = temp

        i = i + 1
        temp = temp.next
    return modularNode

if __name__ == '__main__':
    head = newNode(1)
    head.next = newNode(3)
    head.next.next = newNode(5)
    head.next.next.next = newNode(7)
    head.next.next.next.next = newNode(9)
    k = 2
    answer = modularNode(head, k)
    print("Modular node is", end = ' ')
    if (answer != None):
        print(answer.data, end = ' ')
    else:
        print("None")

Output
Modular node is 7

Time Complexity To Find Modular Node In Linked List: O(n), as we are traversing the complete length of the list

This blog discusses the best way to find modular node in linked List. Linked list is a must practice topic to prepare for the data structures. Our experts have made the most asked questions for the interview’s questions for linked list, you can follow this link Linked List for practicing more questions of linked list.

FAQ

1. What is a modular node in the linked list?
A modular node is the last node of the linked list whose Index is divisible by the number k, i.e. i%k==0.

2. How do you find the last node in a linked list?
The last node of a linked list has the reference pointer as NULL. i.e. node=>next = NULL. To find the last node, we have to iterate the linked till the node=>next != NULL.

3. What is the last node called?
The first node is called the head; it points to the first node of the list and helps us access every other element in the list. The last node, also sometimes called the tail, points to NULL which helps us in determining when the list ends.