Last Updated on April 19, 2022 by Ria Pathak

Introduction
The linked list is one of the most important concepts and data structures to learn while preparing for interviews. Having a good grasp of a linked list can be a huge plus point in coding interviews.
Problem Statement
In this problem, we are given a sorted singly linked list and a value k, our task is to find the pairs whose sum is equal to K.
Note: we can consider a node in one pair only.
Example:
Input : head → 0 → 2 → 3 → 7 → 8 → 10 , K = 10.
Output:
0 10
2 8
7 3
Problem Statement Understanding
Let’s first understand the problem statement with the help of examples.
Let’s say we are given the sorted linked list : head -> 1 -> 1 -> 2 -> 4 -> 6 -> 7 -> NULL and K = 8.
- Then here, we will make a pair of the first 1 with 7.
- After that we cannot make a pair of the 2nd 1 with 7 because this 7 has been already used in one of the pairs.
- Now we have a pair of 2 and 6.
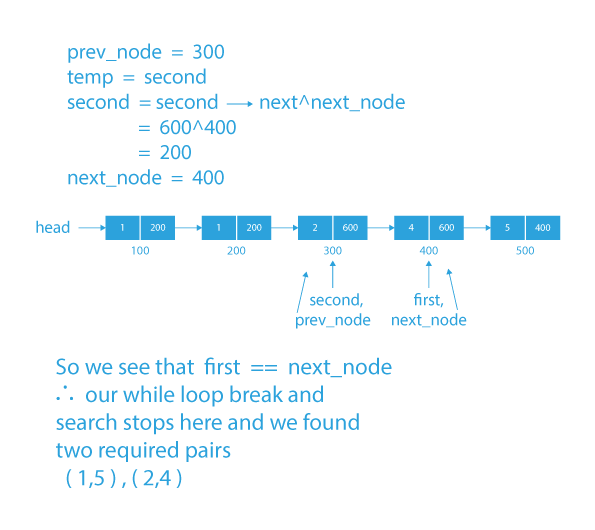
- So our answer pairs would be (1,7) and (2,6).
Let’s move to the next section to see this process in more depth.
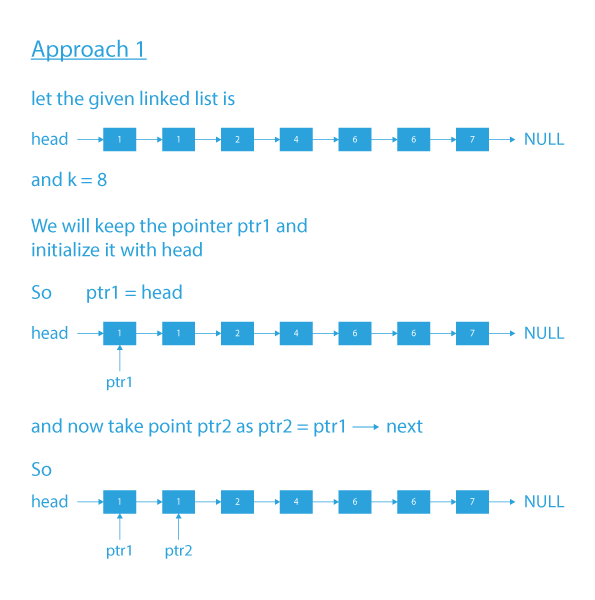
Approach 1
The naive way to do this problem is to traverse over each element one by one and search for the second element in the remaining linked list in a forwarding direction whose sum with the first value is equal to the given value K.
Algorithm
- Take two-pointer ptr1 and ptr2 pointing to head initially.
- Take ptr1→data as the first value and search for the K – (ptr1→data) as the second value in the remaining linked lists in the forwarding direction.
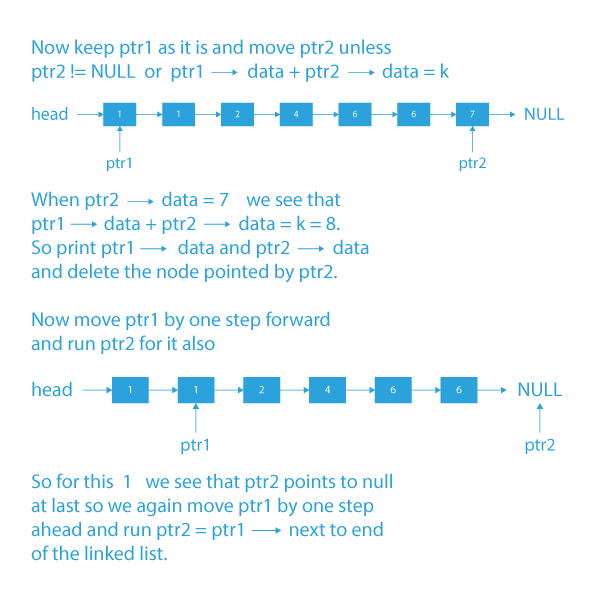
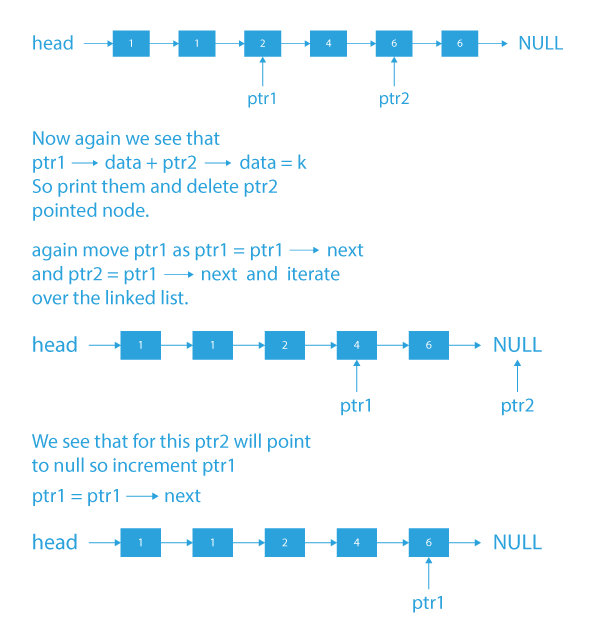
- We find the K-(ptr1->data) using a pointer ptr2. So if there exists a ptr2 such that ptr1->data + ptr2->data == k then we print ptr1->data and ptr2->data and delete node pointed by ptr2 as we mentioned in the problem statement that one node should be considered in only one pair.
- So if we don’t delete ptr2 then it may be counted again for some other duplicate ptr1->data.
- Like in the example linked list head -> 1 -> 1 -> 2 -> 4 -> 6 -> 7 -> NULL and k = 8 here 7 can be considered in for both 1’s if we don’t delete it after considering it once.
- Now, increment ptr1 = ptr1→next and assign ptr1 to ptr2 because in search of the second element the ptr2 reaches the end of the linked list.
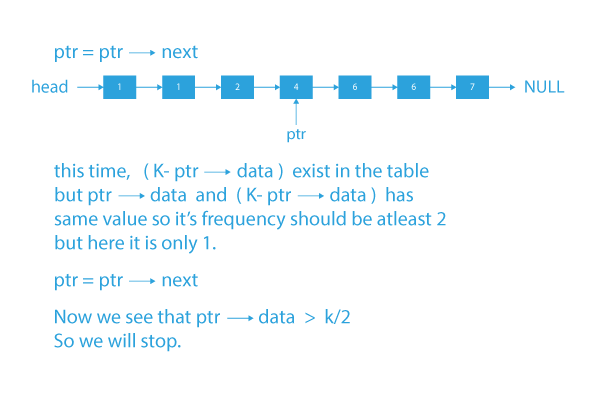
- Do the same work for every element till ptr1→data <= K/2, because if we are traversing for nodes that have ptr1→data greater than K/2 then we have to search for value K – (ptr1→data) that is smaller than ptr1→data, and it is impossible to find that value in remaining linked list which is sorted.
Time Complexity: O(N2), because for every element, we are searching for its pair.
Space Complexity: O(1), No extra space is used.
Dry Run for approach 1
For better understanding follow dry run along with code

Approach 2
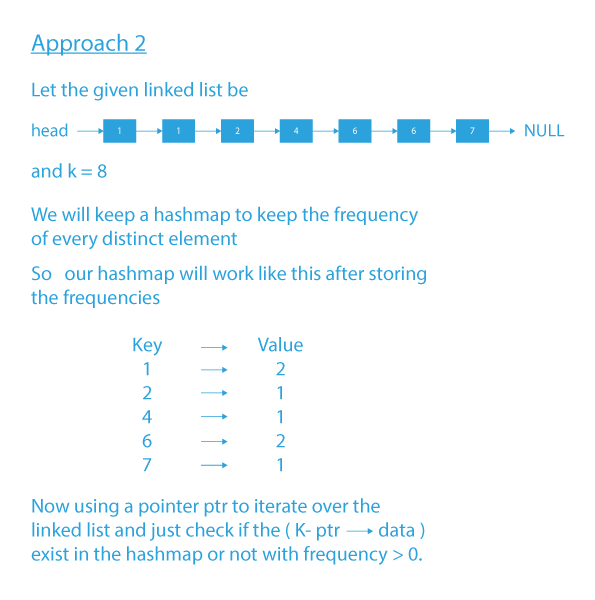
We can apply some optimization to our previous approach by using hashtable/map.
Algorithm
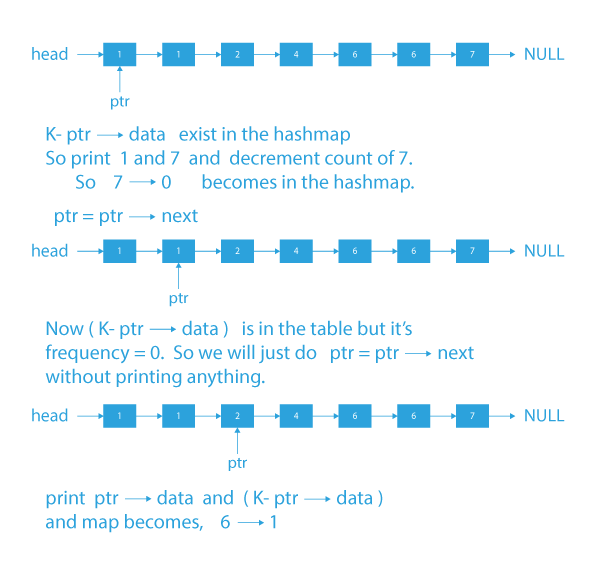
- We will insert every value of the sorted linked list as a key in the hashtable/map. And keep the count of occurrences of every distinct value.
- Take a pointer ptr1 initially pointing to the head.
- We will start traversing over every element of the linked list till ptr1→datadata) is present in the hashtable and its frequency is more than one then print ptr1->data and (K – ptr1->data).
- And decrement the occurrence of (K – ptr1->data) to ensure that the same element is not counted in more than one pair.
- And if ptr->data == (k-ptr->data) then the frequency of ptr->data should be more than 1 to be considered as a valid pair. And we will print ptr->data and (k-ptr->data) (ptr->data)/2 times.
Time Complexity: O(N), because for every element, we are searching for its pair and searching in the hashtable is O(1).
Space Complexity: O(N) because we are keeping a hashtable.
Dry Run for approach 2
For better understanding follow dry run along with code
Finally, we have optimized our solution and now our time complexity is O(N) but we are using extra space which is against the problem statement because we have to find all the pairs whose sum is equal to K without using extra space.
Approach 3
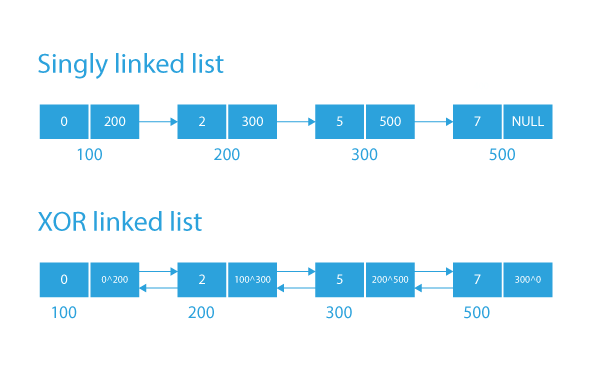
The efficient solution to this problem is to use an XOR linked list.
In a singly linked list, we can traverse the list only in the forward direction. But if we use XOR concept to convert a singly linked list to doubly linked list then we can travel in the singly-linked in both directions.
Now we will use the concept of two pointers because we can move in both directions by exploiting the property of XOR.
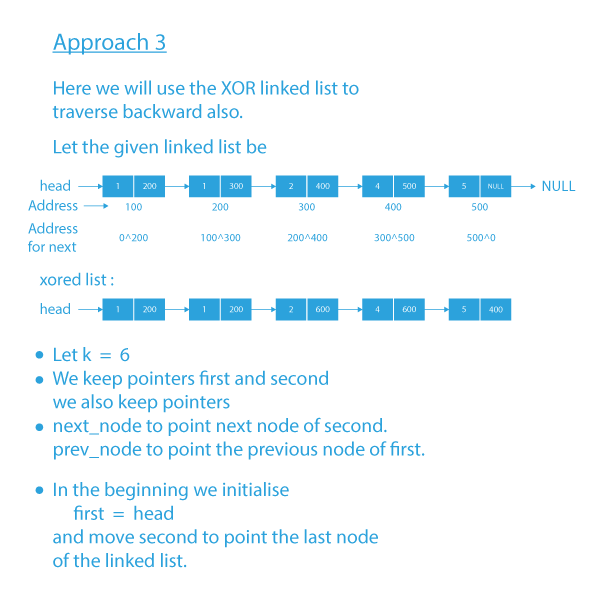
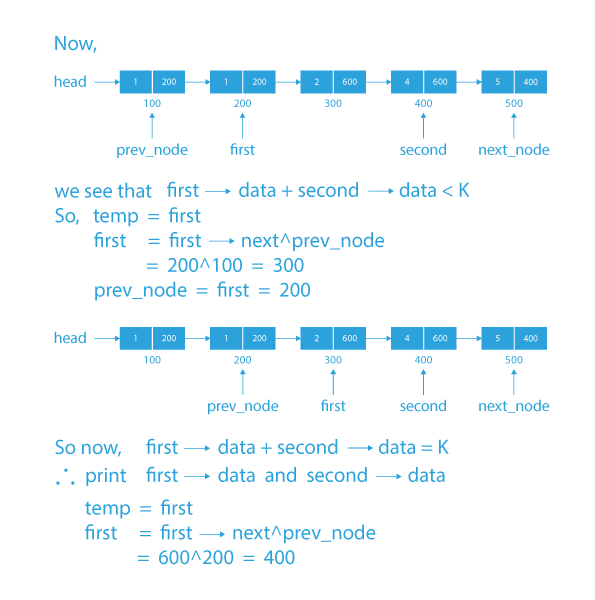
So the main idea here is that since the linked list is sorted, we will keep a pointer ptr1 at the beginning of the list and another pointer ptr2 at the end of the list.
And now if ptr1->data + ptr2->data data+ptr2->data hence we will move ptr1=ptr1->next.
If ptr1->data + ptr2->data > k then it means that we have to decrease the sum ptr1->data + ptr2->data hence we will move ptr2 one step backward analogous to ptr2–.
And if ptr1->data + ptr2->data == K__ then we have found one required pair so print them and move ptr1 to point to the next node and ptr2 to point to one previous node.
Algorithm
- We know that in the singly linked list we have only the address of the next node not of the previous node, so we have to convert our singly linked list into a doubly linked list.
- The doubly linked list we are talking about here is XOR linked list, which is also known as memory efficient doubly linked list.
- The next pointer of each node in the XOR linked list contains the XOR of the previous node’s address and the next node’s address.
- After converting singly linked list into XOR linked list we will initialize two pointers ptr1 and ptr2 variables the ptr1 will be assigned with the head and the ptr2 will be assigned with the last node’s address.
- If ptr1→data + ptr2→data == K then print both ptr1→data and ptr2→data,but if ptr1→data + ptr2→data > K then we move ptr2 in backward direction by find out the address of the previous node using xor’s property and if ptr1→data + ptr2→data < K then we move ptr1 in forward direction.
- The above action will execute till ptr1 == ptr2.
Dry Run for approach 3
For better understanding follow dry run along with code

Code Implementation
#include#include #include #include struct Node { int data; /* also contains XOR of next and previous node after conversion*/ struct Node* next; }; /* Given a reference (pointer to pointer) to the head of a list and an int, push a new node on the front of the list. */ void insert(struct Node** head_ref, int new_data) { /* allocate node */ struct Node* new_node = (struct Node*) malloc(sizeof(struct Node)); /* put in the data */ new_node->data = new_data; /* link the old list off the new node */ new_node->next = (*head_ref); /* move the head to point to the new node */ (*head_ref) = new_node; } /* returns XORed value of the node addresses */ struct Node* XOR (struct Node *a, struct Node *b) { return (struct Node*) ((uintptr_t)a ^ (uintptr_t)b); } // Utility function to convert singly linked list // into XOR doubly linked list void convert(struct Node *head) { // first we store address of next node in it // then take XOR of next node and previous node // and store it in next pointer struct Node *next_node; // prev node stores the address of previously // visited node struct Node *prev = NULL; // traverse list and store xor of address of // next_node and prev node in next pointer of node while (head != NULL) { // address of next node next_node = head->next; // xor of next_node and prev node head->next = XOR(next_node, prev); // update previous node prev = head; // move head forward head = next_node; } } // function to Find pair whose sum is equal to // given value x void pairSum(struct Node *head, int x) { // initialize first struct Node *first = head; // next_node and prev node to calculate xor again // and find next and prev node while moving forward // and backward direction from both the corners struct Node *next_node = NULL, *prev = NULL; // traverse list to initialize second pointer // here we need to move in forward direction so to // calculate next address we have to take xor // with prev pointer because (a^b)^b = a struct Node *second = head; while (second->next != prev) { struct Node *temp = second; second = XOR(second->next, prev); prev = temp; } // now traverse from both the corners next_node = NULL; prev = NULL; // here if we want to move forward then we must // know the prev address to calculate next node // and if we want to move backward then we must // know the next_node address to calculate prev node bool flag = false; while (first != NULL && second != NULL && first != second && first != next_node) { if ((first->data + second->data)==x) { printf("(%d",first->data); printf(",%d",second->data); printf(")"); flag = true; // move first in forward struct Node *temp = first; first = XOR(first->next,prev); prev = temp; // move second in backward temp = second; second = XOR(second->next, next_node); next_node = temp; } else { if ((first->data + second->data) < x) { // move first in forward struct Node *temp = first; first = XOR(first->next,prev); prev = temp; } else { // move second in backward struct Node *temp = second; second = XOR(second->next, next_node); next_node = temp; } } } if (flag == false) printf("No pair found\n"); } // Driver program to run the case int main() { /* Start with the empty list */ struct Node* head = NULL; int x = 17; /* Use insert() to construct below list 3-->6-->7-->8-->9-->10-->11 */ insert(&head, 11); insert(&head, 10); insert(&head, 9); insert(&head, 8); insert(&head, 7); insert(&head, 6); insert(&head, 3); // convert singly linked list into XOR doubly // linked list convert(head); pairSum(head,x); return 0; }
// find XOR of previous and next node address
struct Node* XOR (struct Node *a, struct Node *b){
return (struct Node*) ((uintptr_t) (a) ^ (uintptr_t) (b));
}
// convert singly linked list to XOR linked list
void convertSinglyToXORlist(struct Node *head){
struct Node *next_node;
struct Node *prv = NULL;
while (head != NULL){
next_node = head->next; //next node
head->next = XOR(next_node, prv);// finding XOR of prv and next Node
prv = head;
head = next_node;
}
}
void pairSumToK(struct Node *head, int K){
//both first and second pointer initialized with head
struct Node *first = head;
struct Node *second = head;
struct Node *next_node = NULL, *prv_node = NULL;
while (second->next != prv_node){
struct Node *temp = second;
second = XOR(second->next, prv_node);
prv_node = temp;
}
next_node = NULL;
prv_node = NULL;
while (first != NULL && second != NULL && first != second && first != next_node){
if ((first->data + second->data)==K){
// sum of first Node and second Node's data is equal to K
// then print its value
cout<<first->data<<" "<<second->data<<endl; struct="" node="" *temp="first;" first="XOR(first-">next,prv_node);
prv_node = temp;
temp = second;
second = XOR(second->next, next_node);
next_node = temp;
}
else
{
if ((first->data + second->data) < K){
// if sum of first and second node's data is smaller than k
// move first pointer forward
struct Node *temp = first;
first = XOR(first->next,prv_node);
prv_node = temp;
}
else{
// if sum of first and second node's data is greater than k
// move second pointer backward
struct Node *temp = second;
second = XOR(second->next, next_node);
next_node = temp;
}
}
}
}
Output
(1,7)
(2,6)
Time Complexity: O(N), because we have traversed through every node of the linked list.
[forminator_quiz id=”4869″]
So, in this blog, we have learned to Find pairs for a given sum in a sorted singly linked list without extra space, and in this process, we also learn how to build intuition regarding any problem and how to optimize the solution. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.


