Last Updated on November 28, 2022 by Prepbytes

This article discusses an important topic “find n/k th node in linked list”. “find n/k th node in linked list” is a good topic if you want to master the data structures. Linked List always remain the main bone of data structures and by conquering “find n/k th node in linked list” will make your linked list even more stronger and make it crystal clear to you.
How To Find n/k Th Node In Linked List
In this problem, we have been given a linked list and positive integer k. Our task is to write a function that accepts the head node of the linked list as a parameter and returns the value of the node present at (ceil(n/k))th position in the linked list.
Here, n is the count of the number of nodes in the linked list.
Let’s try to understand the problem with help of examples.
Suppose we are given a linked list

Now according to the problem statement we have to find the node at (ceil(n/k))th position in the linked list and return its value.
For the above given linked list n = 6, as there are 6 nodes in the linked list, so
- (ceil(n/k)) = (ceil(6/4)) = 2, it means that we have to return the value of 2nd node of the linked list as output.
Output: B
Explanation: We will return B in output as B is the value of (ceil(n/k))th node of the above given linked list.
If the linked list is

For the above linked list n = 9 (as there are 9 nodes in the linked list), then the value of (ceil(n/k)) is:
- (ceil(n/k)) = (ceil(9/3)) = 3, so we will return the value of the 3rd node of the linked list as output.
Output: C
Note: Here in this problem we are considering 1 based indexing.
Some more Examples
Input:

Output: 5
Input:

Output: 60
Input:

Output: 18
Now I think from the above examples the problem is clear, and now we have to think how we can approach it.
Approach 1 To Find n/k Th Node In Linked List
A simple approach is:
- First, loop through the linked list to find the count of number of nodes n present in the linked list.
- Then calculate the value of (ceil(n/k)).
- Now starting from the first node of the list traverse to this position given by (ceil(n/k)) and return the data of the node at this position.
Time Complexity To Find n/k Th Node In Linked List: O(n), as we are traversing the complete length of the list.
Space Complexity To Find n/k Th Node In Linked List: O(1)
This approach traverses the linked list 2 times. Let’s try to think, can we do better than this? Can we find out the (ceil(n/k))th node of the linked list in one single traversal?
Let’s see the approach 2 to get the answers to the above questions.
Approach 2 To Find n/k Th Node In Linked List
In this approach, we can get the required node by traversing the list once only. The complete algorithm for this approach is explained below.
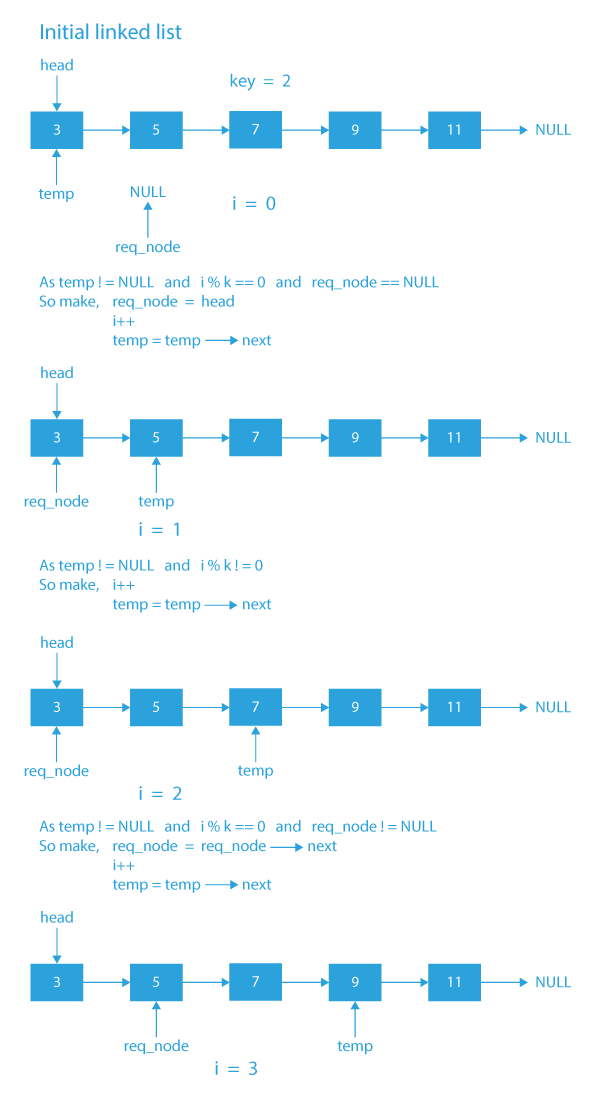
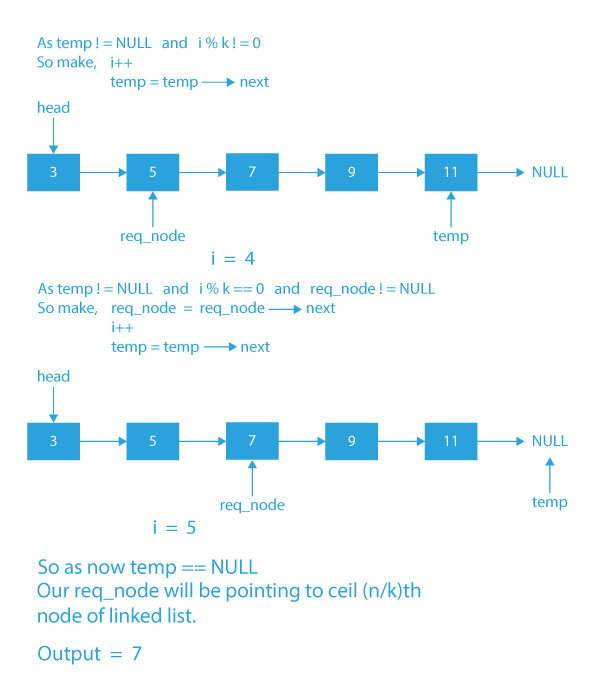
Algorithm To Find n/k Th Node In Linked List
- If k<=0 or our head==NULL, then return NULL.
- We will take two pointers temp and req_node and initialize temp with head and req_node with NULL.
- For every k jumps of the temp pointer, we will make one jump of the req_node pointer.
- Now when temp will be at NULL, req_node will be at (ceil(n/k))th node of the linked list.
- Finally, we will return the req_node->data as output.
Dry Run To Find n/k Th Node In Linked List
## Code Implementation To Find n/k Th Node In Linked List:
#include#include struct Node { int data; struct Node* next; }; struct Node* newNode(int x) { struct Node* node = malloc(sizeof(struct Node*)); node->data = x; node->next = NULL; return node; } struct Node* fractionalNodes(struct Node* head, int k) { if (k <= 0 || head == NULL) return NULL; struct Node* req_node = NULL; int i = 0; for (struct Node* temp = head; temp != NULL; temp = temp->next) { if (i % k == 0) { if (req_node == NULL) req_node = head; else req_node = req_node->next; } i++; } return req_node; } void printList(struct Node* node) { while (node != NULL) { printf("%d ", node->data); node = node->next; } printf("\n"); } int main(void) { struct Node* head = newNode(3); head->next = newNode(5); head->next->next = newNode(7); head->next->next->next = newNode(9); head->next->next->next->next = newNode(11); int k = 2; printf("List is "); printList(head); struct Node* answer = fractionalNodes(head, k); printf("\nFractional node is "); printf("%d\n", answer->data); return 0; }
#includeusing namespace std; struct Node { int data; Node* next; }; Node* newNode(int data) { Node* new_node = new Node; new_node->data = data; new_node->next = NULL; return new_node; } Node* fractionalNodes(Node* head, int k) { if (k <= 0 || head == NULL) return NULL; Node* req_node = NULL; int i = 0; for (Node* temp = head; temp != NULL; temp = temp->next) { if (i % k == 0) { if (req_node == NULL) req_node = head; else req_node = req_node->next; } i++; } return req_node; } void printList(Node* node) { while (node != NULL) { printf("%d ", node->data); node = node->next; } printf("\n"); } int main(void) { Node* head = newNode(3); head->next = newNode(5); head->next->next = newNode(7); head->next->next->next = newNode(9); head->next->next->next->next = newNode(11); int k = 2; printf("List is "); printList(head); Node* answer = fractionalNodes(head, k); printf("\nFractional node is "); printf("%d\n", answer->data); return 0; }
public class FractionalNode
{
static class Node{
int data;
Node next;
Node (int data){
this.data = data;
}
}
static Node fractionalNodes(Node head, int k)
{
// Corner cases
if (k <= 0 || head == null)
return null;
Node fractionalNode = null;
// Traverse the given list
int i = 0;
for (Node temp = head; temp != null;temp = temp.next)
{
if (i % k == 0){
// First time we see a multiple of k
if (fractionalNode == null)
fractionalNode = head;
else
fractionalNode = fractionalNode.next;
}
i++;
}
return fractionalNode;
}
static void printList(Node node)
{
while (node != null)
{
System.out.print(node.data+" ");
node = node.next;
}
System.out.println();
}
public static void main(String[] args) {
Node head = new Node(3);
head.next = new Node(5);
head.next.next = new Node(7);
head.next.next.next = new Node(9);
head.next.next.next.next = new Node(11);
int k =2;
System.out.print("List is ");
printList(head);
Node answer = fractionalNodes(head, k);
System.out.println("Fractional node is "+answer.data);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(data):
new_node = Node(data)
new_node.data = data
new_node.next = None
return new_node
def fractionalNodes(head, k):
if (k <= 0 or head == None):
return None
fractionalNode = None
i = 0
temp = head
while (temp != None):
if (i % k == 0):
if (fractionalNode == None):
fractionalNode = head
else:
fractionalNode = fractionalNode.next
i = i + 1
temp = temp.next
return fractionalNode
def printList(node):
while (node != None):
print(node.data, end = ' ')
node = node.next
if __name__ == '__main__':
head = newNode(3)
head.next = newNode(5)
head.next.next = newNode(7)
head.next.next.next = newNode(9)
head.next.next.next.next = newNode(11)
k = 2
print("List is", end = ' ')
printList(head)
answer = fractionalNodes(head, k)
print("\nFractional node is", end = ' ')
print(answer.data)
Output
List is 3 5 7 9 11
Fractional node is 7
**Time Complexity To Find n/k Th Node In Linked List:** O(n), as we are traversing the complete length of the list
This article discusses the question “Find n/k Th Node In Linked List” by two different approaches. Coding Questions like “Find n/k Th Node In Linked List” will always help in achieving the long term goals. Don’t stop here for practicing more questions of linked list, you can follow this link Linked List.
## FAQ
**1. How do you find the kth node from the end in a linked list?**
We will use the following property to find the kth node from the end. Kth node from end = (cnt-k+1)th node from the beginning. Let us store the value of cnt-k+1 in a variable ‘n’. Now traverse the linked list again and return the pointer to the ‘nth’ node.
**2. How do you find the common node between two linked lists?**
Compare every node of list A with every node of list B. If the node is a match then increment the count and return count after all the nodes get compared.
**3. Which companies have recently asked “Find n/k Th Node In Linked List” in their interviews?**
Tech Companies Samsung, Reliance JIO, TCS, Amazon, Accenture and Infosys have recently asked this question in the interview round for freshers.


