Merge two sorted linked lists (in-place)

Last Updated on November 22, 2022 by Prepbytes

In this article, we will learn how to merge two sorted linked lists. Sorting is defined as the technique of arranging the elements either in ascending or descending order. let’s try to understand how we can approach merge 2 sorted linked list.

How to Merge 2 Sorted Linked List

In this problem, we will be given two sorted linked lists. We need to merge both lists such that the newly created list is also in sorted order.

The problem statement is quite straightforward, we will get two linked lists that are sorted in nature, and then we need to form a linked list using all the nodes of both linked lists such that the newly formed list is sorted in order.

Note: Remember that we cannot use any extra space, as we need to do this in place.

Let’s try to understand how to merge two sorted linked lists more clearly using examples.

Let the two sorted lists given to us be

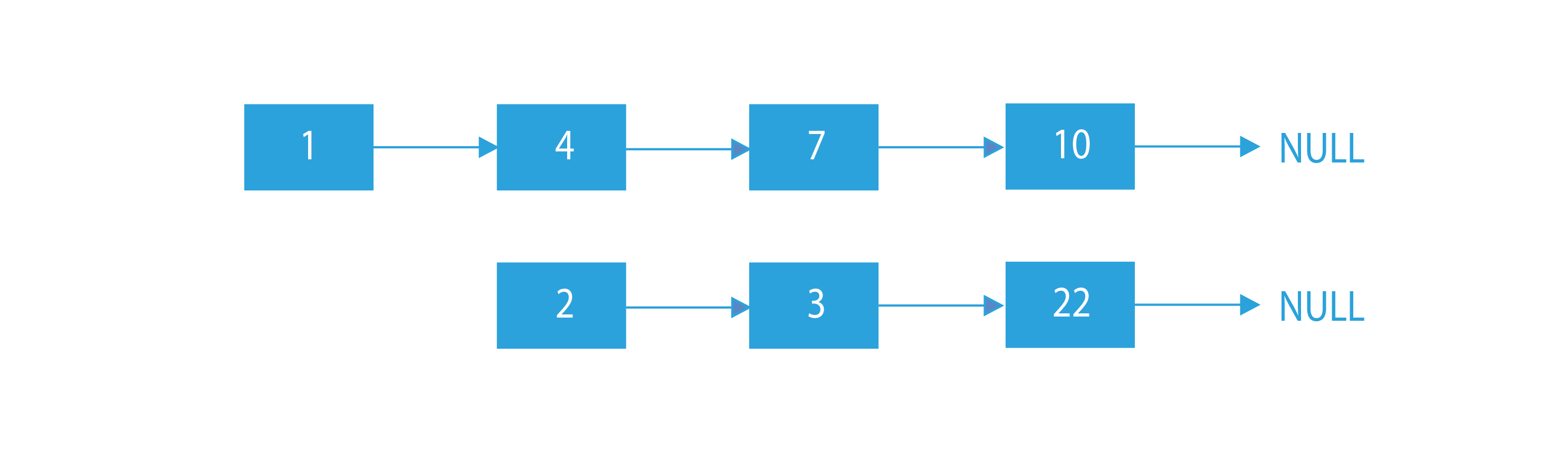
• Now, the list that we need to return must contain all the nodes of both lists in sorted order.
• So, the newly formed list should be:

Let’s take another example:
Let the two sorted lists given to us be 2→8→9→10→NULL and 11→13→17→NULL

• For the above two sorted lists, the final linked list after merging will be 2→8→9→10→11→13→17→NULL

Some more examples of merge two sorted linked lists

Sample Input 1:

• list 1: 1→2→5→10→NULL
• list 2: 3→7→9→11→NULL

Sample Output 1: 1→2→3→5→7→9→10→11→NULL

Sample Input 2:

• list 1: 2→3→9→10→NULL
• list 2: 4→5→7→8→12→NULL

Sample Output 2: 2→3→4→5→7→8→9→10→12→NULL

At this point, we have understood the problem statement. Now we will try to formulate an approach to merge two sorted linked lists.

• Before moving to the approach section, try to think about how you can merge two sorted linked lists.

If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.

Let’s move to the approach section to merge two sorted linked lists.

Approach 1 to merge 2 sorted linked list

Our approach will be simple:

• We will make a recursive function that will create a sorted list out of two given sorted lists.
• If both the heads of the linked lists are NULL, return NULL and if only one head is NULL, then return the other head.
• We will compare the head of both the lists and the one with a smaller head will be appearing at the current position and all other nodes will appear after that.
• Now call the recursive function again with parameters as the next node of the list having a smaller head value and the head of the other list.
• Our recursive call will be returning the next smaller element of the linked lists attached with the rest of the sorted list. Make the next of the current node point to the list returned by the recursive function (curr_node-> next = recursive function()).

Following all the above steps, we will have our merged sorted list containing nodes of all the given linked lists in sorted order.

Algorithm 1 to merge two sorted linked lists

1) The recursive function will have two parameters, i.e., head1 and head2, denoting the current head node of the first and second list, respectively.
2) Base case:

• If both of the head nodes are NULL, return NULL from there.
• If one of the head nodes is NULL, but the other one is not NULL, return the other head.
  3) If head1’s data is less than head2’s data, assign head1’s next to the result returned by the recursive function having parameters head1→next and head2 and then return head1.
  4) Else, assign head2’s next to the result returned by the recursive function having parameters head1 and head2→next and then return head2.

Time Complexity: O(n), n is the number of nodes in both list combined.
Space Complexity: O(n), n is the size of the recursive stack

The above approach works fine, but can we make our code more efficient in memory?

• The answer is yes, and to know it, have a look at the helpful observations and also read the below approach which uses constant memory.

Helpful Observations to merge 2 sorted linked list

• If we observe, we can see that we need two pointers at the beginning of both list since the smallest value will be present at the beginning of both lists.
• The list has a smaller first node that will be considered as the first list and the other one would be considered the second list.
• We then have to just insert the second pointer node between the first and its next node if its value lies between the first and its next node.
• If that is not the case, then we just need to move forward in iteration.

Applying the above observations, we can easily create the new sorted linked list.

Approach 2 to merge two sorted linked lists

Taking help from the observation explained above, let us understand the approach to merge two sorted linked lists with the help of an example.

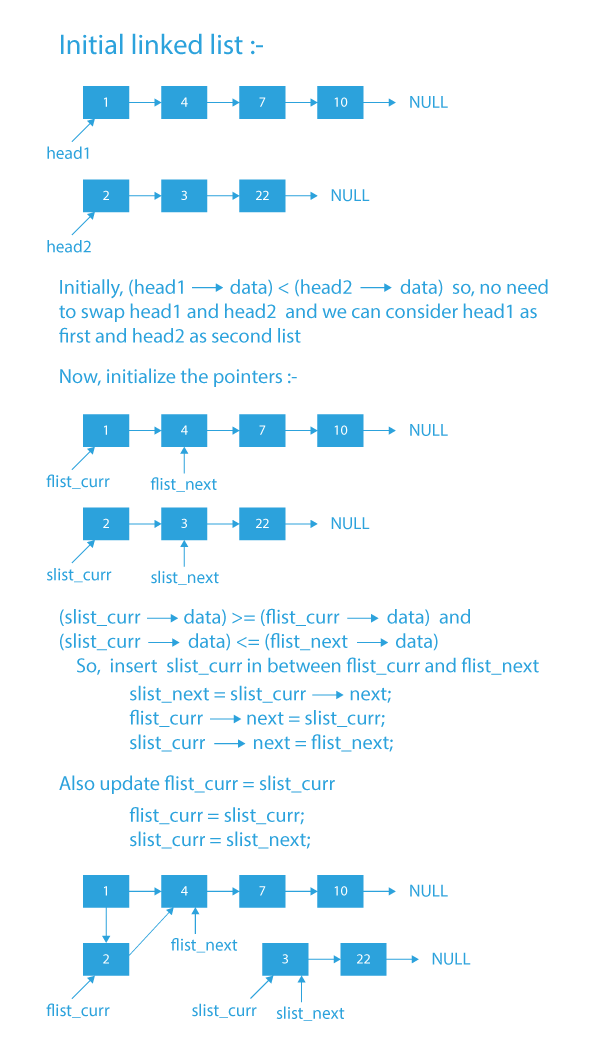
• Let the input lists be 1→4→7→10→NULL and 2→3→22→NULL
• We would keep two pointers – one at the start of each linked list.
• Now, the first pointer will point to ‘1’ because the first list has a smaller first node, and the second one will point to ‘2’ because it has a greater first node.
• Since the second pointer’s data lies between ‘1’ and ‘4’ (first pointer’s data and next of first pointer’s data), so we insert it between ‘1’ and ‘4’.
• After inserting the second node, we update the head of the second list to its next node.
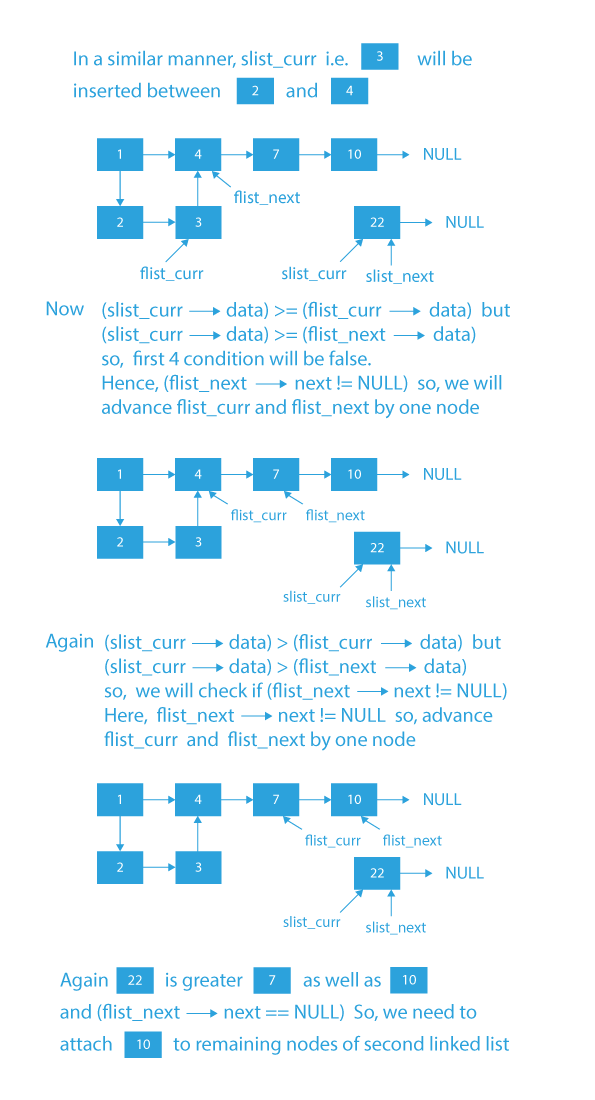
• Now let’s suppose the value of the second pointer was greater than ‘4’ so, we would not do anything in this case and just move our first pointer forward by one node.

Now, let’s formulate an algorithm based on the approach discussed above and handle the edge cases that might be present while implementing the code.

Algorithm 2 to merge two sorted linked lists

• Find which list has a smaller first node and consider it as the first list and the other one as the second list (flist stands for first list and slist stands for second list).
• Now, initialize four pointers:
  • First will point to the head of the first list ( say flist_curr ).
  • The second will point to the second node of the first list ( say flist_next ).
  • The third will point to the head of the second list ( say slist_curr ).
  • The Fourth will point to the second node of the second list ( say slist_next ).
• While iterating through the lists, we need to check if slist_curr’s value lies between flist_curr’s value and flist_next’s value.
  a) If its value lies in between, then we need to insert the slist_curr node in between flist_curr and flist_next and update flist_curr to slist_curr and slist_curr to slist_next.
  b) Else, we will check if there are more nodes in the first list.
  • If there are more nodes in the first list, then just move flist_curr and flist_next to their respective next nodes.
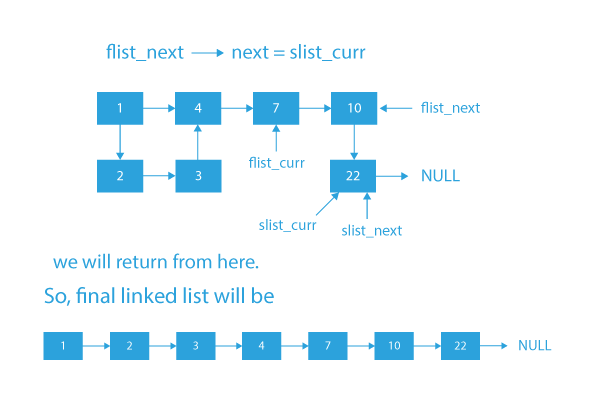
  • If that is not the case, then the last node of the first node should point to the remaining nodes of the second list, and then finally, we will return the head of the first list.
• After performing the above steps, we would get our new list that is sorted.

### Dry Run to merge two sorted linked lists

## Code Implementation to merge two sorted linked lists

#include <stdio.h>
#include<stdbool.h>
#include<stdlib.h>
 
struct Node {
    int data;
    struct Node* prev;
    struct Node* next;
};

void push(struct Node **head_ref, int data)
{
    struct Node* ptr1 =
            (struct Node*) malloc(sizeof(struct Node));
    struct Node *temp = *head_ref;
    ptr1->data = data;
    ptr1->next = *head_ref;
    if (*head_ref != NULL)
    {
        while (temp->next != *head_ref)
            temp = temp->next;
        temp->next = ptr1;
    }
    else
        ptr1->next = ptr1; 
 
    *head_ref = ptr1;
}

void printList(struct Node *head)
{
    struct Node *temp = head;
    if (head != NULL)
    {
        do
        {
            printf("%d ",temp->data);
            temp = temp->next;
        }
        while (temp != head);
    }
}

int main(void)
{
    struct Node *head = NULL;
    push(&head, 15);
    push(&head, 18);
    push(&head, 7);
    push(&head, 1);
 
    printf( "Contents of Circular Linked List\n ");
    printList(head);
}

#include<bits/stdc++.h>
using namespace std;
class Node
{
    public:
    int data;
    Node* next;
    Node(int x){
        data = x;
   next = NULL;
    }
};


void printList(Node *head)
{
    if (!head)
        return;
     
    while (head->next != NULL)
    {
        cout << head->data << " -> ";
        head = head->next;
    }
    cout << head->data << endl;
}
 
Node* mergeTwoSortedLists(Node* head1, Node* head2)
{
    // if first list has only one node
    if (!head1->next) {
        head1->next = head2;
        return head1;
    }
    // make the list with smaller first node as first list
    if((head1->data) > (head2->data)){
        Node *temp = head1;
        head1 = head2;
       head2 = temp;
    }
    // Initialize all four pointer as discussed above in step 1 
    Node *flist_curr = head1, *flist_next = head1->next;
    Node *slist_curr = head2, *slist_next = head2->next;
 
    while (flist_next && slist_curr) {
        // if value of slist_curr lies in between value of flist_curr and
        // value of flist_next then insert slist_curr between flist_curr and 
        // flist_next
        if ((slist_curr->data) >= (flist_curr->data) && (slist_curr->data) <= (flist_next->data)) {
            slist_next = slist_curr->next;
            flist_curr->next = slist_curr;
            slist_curr->next = flist_next;
 
            // update flist_curr to point to slist_curr and slist_curr to point to slist_next
            flist_curr = slist_curr;
            slist_curr = slist_next;
        }
        else {
            // if we have not reached end of first list
            if (flist_next->next) {
                flist_next = flist_next->next;
                flist_curr = flist_curr->next;
            }
 
            // if we have reached the end of the first list then 
            // point last node’s next to remaining nodes of 
            // second list
            else {
                flist_next->next = slist_curr;
                return head1;
            }
        }
    }
    return head1;
}
 
int main(void)
{
    Node* head1 = NULL;
    head1 = new Node(1);
    head1->next = new Node(4);
    head1->next->next = new Node(7);
    head1->next->next->next = new Node(10);
 
    Node* head2 = NULL;
    head2 = new Node(2);
    head2->next = new Node(3);
    head2->next->next = new Node(22);
 
    Node *tmp = mergeTwoSortedLists(head1,head2);
    cout<<"Merged Linked list"<<endl;
    printList(tmp);
    return 0;
}

class MergeInPlace {

    static class Node {
        int data;
        Node next;
    }
    static Node newNode(int key)
    {
        Node temp = new Node();
        temp.data = key;
        temp.next = null;
        return temp;
    }
    static void printList(Node node)
    {
        while (node != null) {
            System.out.print(node.data + " ");
            node = node.next;
        }
    }

    // Merges two lists with headers as h1 and h2.
    // It assumes that h1's data is smaller than
    // or equal to h2's data.
    static Node mergeUtil(Node h1, Node h2)
    {
        // if only one node in first list
        // simply point its head to second list
        if (h1.next == null) {
            h1.next = h2;
            return h1;
        }
        // Initialize current and next pointers of
        // both lists
        Node curr1 = h1, next1 = h1.next;
        Node curr2 = h2, next2 = h2.next;

        while (next1 != null && curr2 != null) {
            // if curr2 lies in between curr1 and next1
            // then do curr1->curr2->next1
            if ((curr2.data) >= (curr1.data) && (curr2.data) <= (next1.data)) {
                next2 = curr2.next;
                curr1.next = curr2;
                curr2.next = next1;

                // now let curr1 and curr2 to point
                // to their immediate next pointers
                curr1 = curr2;
                curr2 = next2;
            }
            else {
                // if more nodes in first list
                if (next1.next != null) {
                    next1 = next1.next;
                    curr1 = curr1.next;
                }

                // else point the last node of first list
                // to the remaining nodes of second list
                else {
                    next1.next = curr2;
                    return h1;
                }
            }
        }
        return h1;
    }
    // Merges two given lists in-place. This function
    // mainly compares head nodes and calls mergeUtil()
    static Node merge(Node h1, Node h2)
    {
        if (h1 == null)
            return h2;
        if (h2 == null)
            return h1;

        // start with the linked list
        // whose head data is the least
        if (h1.data < h2.data)
            return mergeUtil(h1, h2);
        else
            return mergeUtil(h2, h1);
    }
    // Driver code
    public static void main(String[] args)
    {
        Node head1 = newNode(1);
        head1.next = newNode(3);
        head1.next.next = newNode(5);

        // 1->3->5 LinkedList created

        Node head2 = newNode(0);
        head2.next = newNode(2);
        head2.next.next = newNode(4);

        // 0->2->4 LinkedList created

        Node mergedhead = merge(head1, head2);

        printList(mergedhead);
    }
}

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

def newNode(key):

    temp = Node(0)
    temp.data = key
    temp.next = None
    return temp

def printList(node):

    while (node != None) :
        print( node.data, end =" ")
        node = node.next
    
def mergeUtil(h1, h2):

    if (h1.next == None) :
        h1.next = h2
        return h1
    
    curr1 = h1
    next1 = h1.next
    curr2 = h2
    next2 = h2.next

    while (next1 != None and curr2 != None):
    
        if ((curr2.data) >= (curr1.data) and
            (curr2.data) <= (next1.data)) :
            next2 = curr2.next
            curr1.next = curr2
            curr2.next = next1

            curr1 = curr2
            curr2 = next2
        
        else :
            if (next1.next) :
                next1 = next1.next
                curr1 = curr1.next
            
            else :
                next1.next = curr2
                return h1

    return h1

def merge( h1, h2):

    if (h1 == None):
        return h2
    if (h2 == None):
        return h1

    if (h1.data < h2.data):
        return mergeUtil(h1, h2)
    else:
        return mergeUtil(h2, h1)


head1 = newNode(1)
head1.next = newNode(4)
head1.next.next = newNode(7)
head1.next.next.next = newNode(10)


head2 = newNode(2)
head2.next = newNode(3)
head2.next.next = newNode(22)


mergedhead = merge(head1, head2)

print("Merged Linked list")
printList(mergedhead)

Output
Merged Linked list
1 -> 2 -> 3 -> 4 -> 7 -> 10 -> 22

**Time Complexity:** O(n), where n is the number of nodes in the list.

So, in this blog, we have tried to explain how to merge two sorted linked lists. We have explained various approaches with picturised dry runs and code implementation in various languages as well and also explained the optimization of space complexity. To brush up your skills on Linked List, which is you can follow this link Linked Listwhich is curated by our expert mentors at PrepBytes.

## FAQs related to merge two sorted linked lists

**1. How many comparisons would be required to merge two sorted lists?**
To merge two lists of sizes m and n, we need to do m+n-1 comparisons in the worst case.

**2. Why is merge sort important?**
With merge sort, we can efficiently sort a list in O(n*log(n)) time complexity.

**3. What type of approach is used in merge sort ?**
Merge sort is a sorting technique based on the divide and conquer technique. Having worst-case time complexity being Ο(n* log(n)), it is one of the most respected algorithm.