Last Updated on December 13, 2022 by Prepbytes

In this blog, we will learn to create a doubly linked list from ternary tree. So, let’s get started with the creation of a doubly linked list from a ternary tree.
The ternary tree is a data structure with a maximum of three children per node. This is accomplished by traversing the ternary tree in the following order: root -> left child -> middle child ->, right child. To begin, traverse the root node and add it to the list. Then, add its right, middle, and left subtrees.
A Doubly Linked List is a type of linked list that allows easy traversal in both forward and backward directions.
How to create doubly linked list from ternary tree
In this problem, we are given a ternary tree, and we have to convert it to a doubly linked list.
Let’s try to understand the problem statement with the help of examples.
Note: A ternary tree is very much similar to a binary tree, but instead of having two children, it has three children left, middle, and right.
Let’s assume that the given ternary tree is:
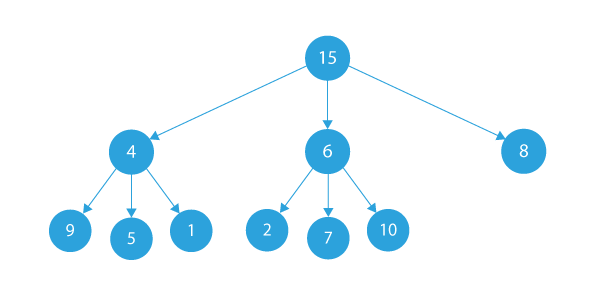
- According to the problem statement, we need to convert this given ternary tree to a doubly linked list.
- After converting the given tree to doubly linked list, our doubly linked list will look like:

Taking another example, if the given ternary tree is:
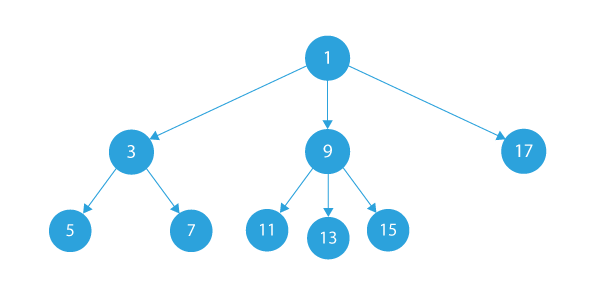
- Then, in this case, after conversion, our doubly linked list will be:

Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Before moving on further, let’s see some helpful observations, which will help us to approach this problem.
Helpful Observations of doubly linked list from ternary tree
Let’s compare the relative position of nodes in the binary tree and doubly linked list.
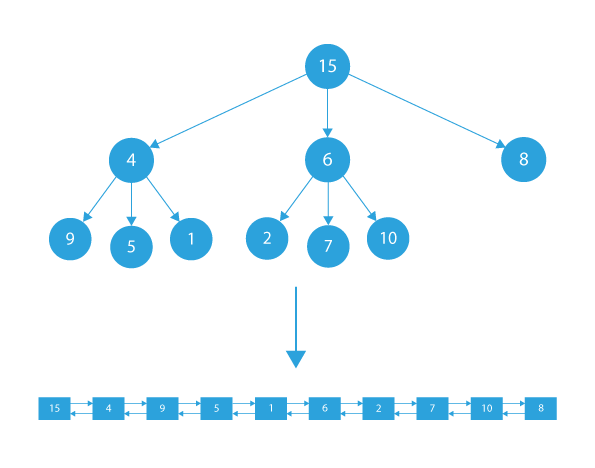
- Node 15 is the root node, so it occurs first in the doubly linked list. It is not part of any subtree rooted at some other node, i.e., it is not a child of any other node.
- In the resultant doubly linked list, node 4 will occur before nodes 9, 5, and 1 as they are children’s of node 4.
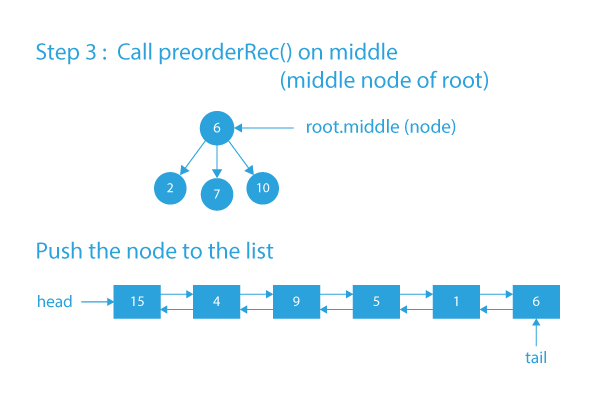
- Similarly, node 6 will occur before nodes 2, 7, and 10 as they are the children’s of node 6.
Hence, it is clear from above observations that every node should be inserted first in the doubly linked list, followed by its children’s.
- If we consider the children’s of node 4, we observe that node 9 is before node 5 and node 5 is before node 1 in the doubly linked list.
- If we consider the children’s of node 6, we observe that node 2 is before node 7 and node 7 is before node 10 in the doubly linked list.
Hence, it is clear from above observations that from children’s, the left child will be inserted first, followed by the mid-child and at last the right child.
In this way, our doubly linked list will be formed.
Approach of doubly linked list from ternary tree
While creating a Doubly Linked List from a ternary tree, the Doubly Linked List must follow the following properties:
- The left pointer of a node in ternary tree will act a prev pointer in the Doubly Linked List.
- The right pointer of a node in ternary tree will act a next pointer in the Doubly Linked List.
- The middle pointer of a ternary tree node will point to null.
To create a desired Doubly Linked List from the given Ternary tree:
- We need to traverse the given tree using preorder traversal and insert the nodes in our Doubly Linked List following the preorder traversal of the tree.
In preorder traversal, the root is visited first, followed by its left child and then a right child. So, we will add the node to our doubly linked list as soon as it is visited while doing preorder traversal on the given ternary tree.
Algorithm of doubly linked list from ternary tree
-
Create head and tail of the linked list (head will be the starting point of the Doubly Linked List, and tail will store the last node of the Doubly Linked List).
-
Perform a preorder traversal on the given tree.
-
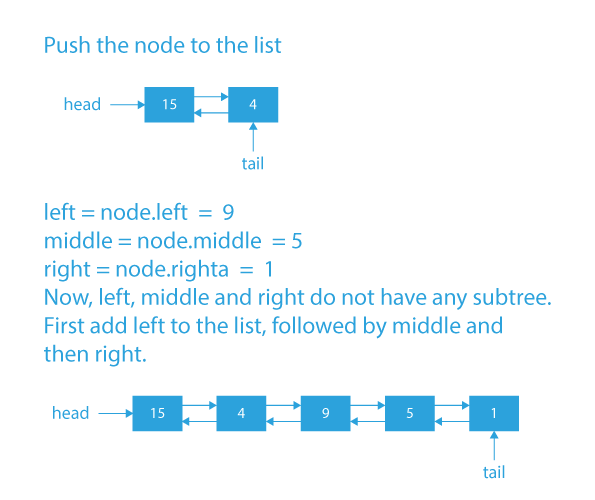
If the node is not present already in our linked list, then insert the node at the tail of the linked list. To insert a node to the list, we will use tail pointer. Suppose we have to add a node to the list, then:
- First, the tail.right will point to node to be inserted (tail.right = node).
- Then node.left will point to tail (node.left = tail).
-
Finally, output the desired Doubly Linked List.
Dry Run of doubly linked list from ternary tree
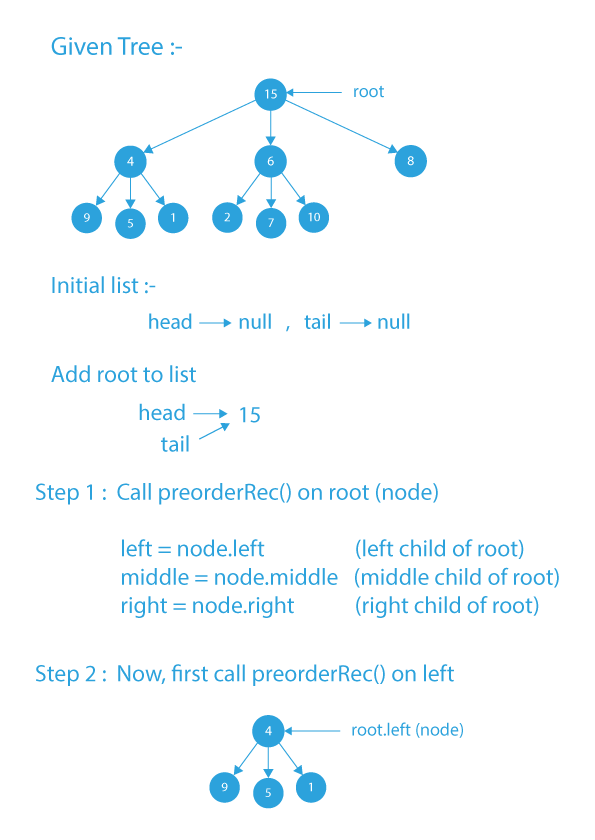

Code Implementation of doubly linked list from ternary tree
public class Prepbytes {
static class treeNode {
int data;
treeNode left, middle, right;
public treeNode(int data) {
this.data = data;
left = middle = right = null;
}
}
static treeNode tail;
public static void push(treeNode node) {
tail.right = node;
node.left = tail;
node.middle = node.right = null;
tail = node;
}
/* This is a recursive method to perform preorder traversal on the ternary tree. */
public static void preorderRec(treeNode node, treeNode head) {
if (node == null)
return;
treeNode left = node.left;
treeNode middle = node.middle;
treeNode right = node.right;
if (tail != node) {
push(node);
}
preorderRec(left, head);
preorderRec(middle, head);
preorderRec(right, head);
}
/* This method is used to start the preorder traversal on the ternary tree. */
public static treeNode startPreorderTraversal(treeNode root) {
treeNode head = root;
tail = root;
preorderRec(root, head);
return head;
}
/* This method is used to print the final doubly linked list once all the nodes from the ternary tree have been added to it. */
public static void printList(treeNode head) {
while (head != null) {
if (head.right != null) {
System.out.print(head.data + " ");
} else {
System.out.print(head.data);
}
head = head.right;
}
}
public static void main(String args[]) {
treeNode root = new treeNode(15);
root.left = new treeNode(4);
root.middle = new treeNode(6);
root.right = new treeNode(8);
root.left.left = new treeNode(9);
root.left.middle = new treeNode(5);
root.left.right = new treeNode(1);
root.middle.left = new treeNode(2);
root.middle.middle = new treeNode(7);
root.middle.right = new treeNode(10);
treeNode head = startPreorderTraversal(root);
System.out.println("Converted Doubly linked list");
printList(head);
}
}
Output
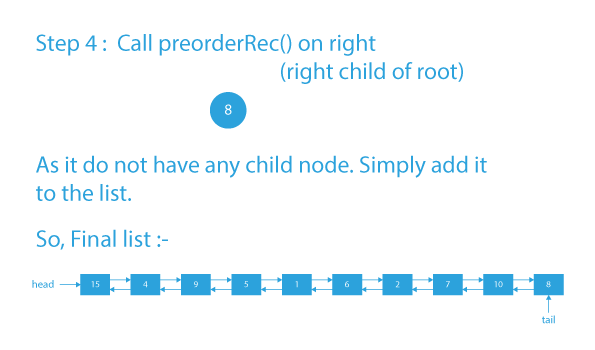
Converted Doubly linked list
15 4 9 5 1 6 2 7 10 8Time Complexity of doubly linked list from ternary tree: O(n), where n is the total number of nodes in the given tree. We are traversing the tree which takes linear time.
Conclusion
In this article, we have discussed how we can create a doubly linked list from ternary tree. We started by introducing the ternary tree, a doubly linked list, and the problem statement. This is one of the good problems that help you strengthen your concepts in LinkedList and if you want to practice more such problems, you can check out Prepbytes (Linked List).
FAQs related to doubly linked list from ternary tree
1. Is a ternary tree are same as a binary tree?
A ternary tree is a form of tree data structure in computer science that allows each node to have up to three derivative nodes. On the other hand, a binary tree can have one or two derived nodes for each node.
2. What is the real-life application of a ternary tree?
Ternary search trees can be used to hold all of the words in a dictionary. Once the word has been typed into an editor, it may be checked for correct spelling by running it through the ternary search tree in parallel.
3. Is it possible to make a doubly-linked list with just one pointer for each node?
Yes, we can make a doubly-linked list with just one pointer for each node by storing the XOR of the previous and next node’s addresses.


