Last Updated on November 28, 2023 by Ankit Kochar

Welcome to the realm of linked list manipulation! If you’ve ever wondered how to efficiently merge two sorted linked lists in such a way that the resulting list is in reverse order, you’re about to embark on a fascinating journey. Merging linked lists is a common task in programming, but when the requirement is to have the merged list in reverse order, it adds an intriguing twist. In this guide, we’ll delve into the techniques and algorithms to seamlessly merge two sorted linked lists while maintaining that reversed order. Let’s unravel the steps to achieve this and explore the intricacies of linked list manipulation.
How To Merge 2 Sorted Linked List In Reverse Order
In this problem, we are given two sorted linked lists, and we are asked to merge the two lists in such a way that the new merged list is in reverse order.
Let’s try to understand this problem with the help of examples.
If the given linked lists are:
list 1: 3→7→10→14.
list 2: 12→13→15.
- According to the problem statement, we need to merge the list 1 and list 2 in such a way that the final merged list is in the reverse order.
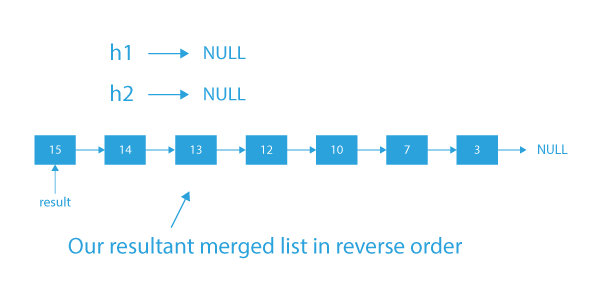
- When we actually merge the list 1 and list 2, our merged list will be 3→7→10→12→13→14→15.
- And our output will be the reverse of this merged list, which is 15→14→13→12→10→7→3.
Taking another example, if the linked lists are:
list 1: 1→2→3→9.
list 2: 4→5→11→17.
- In this case, when we merge list 1 and list 2, our merged list will be 1→2→3→4→5→9→11→17.
- And our output will be the reverse of this merged list, which is: 17→11→9→5→4→3→2→1.
Some more examples
Sample Input 1:
- list 1: 1→3→5→7
- list 2: 2→4→6→8
Sample Output 1:
- 8→7→6→5→4→3→2→1
Sample Input 2:
- list 1: 2→5→10→15
- list 2: 3→6→7
Sample Output 2:
- 15→10→7→6→5→3→2
Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.
Before moving to the approach section, try to think how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Well, the most naive idea is:
- Reverse the first list.
- Reverse the second list.
- And then merge two reversed linked lists.
Using these above steps, we will get our required output.
Another similar approach is first to merge both the list and then finally reverse the merged list.
Both of the above approaches will work fine, but can we do this with some in-place algorithm and only one traversal using O(1) extra space?
- Let’s see the approach for the same.
Let’s move to the approach section.
Approach To Merge 2 Sorted Linked List In Reverse Order
This approach is based on a merge style process.
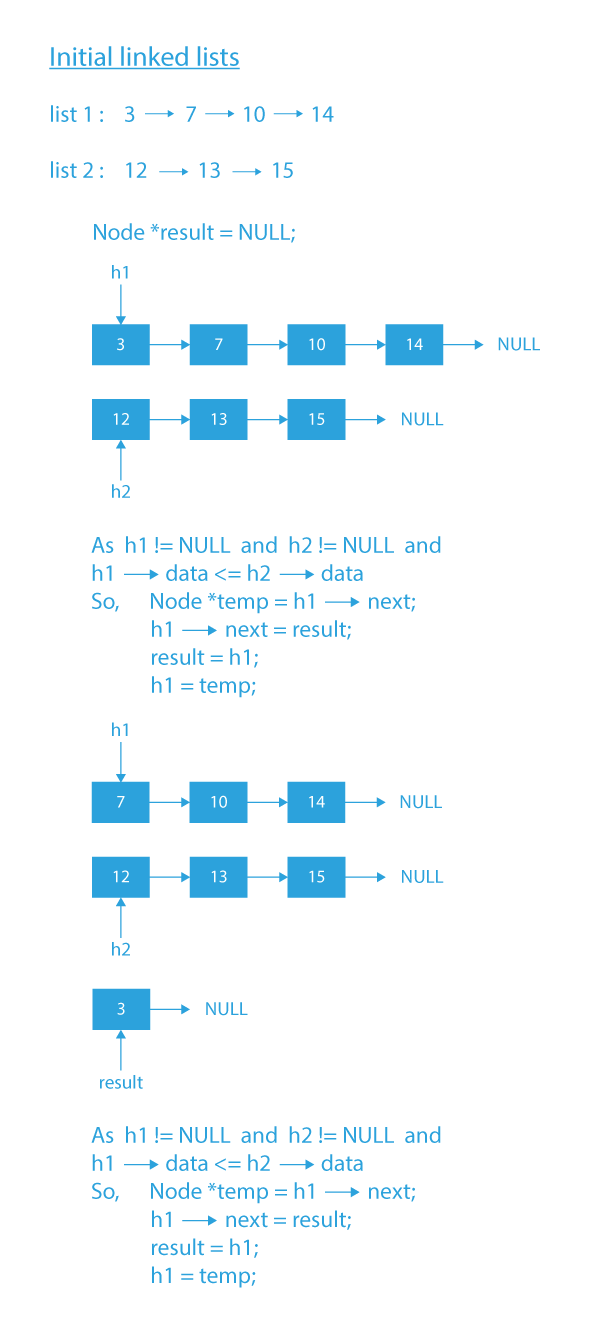
- First, we initialize the resultant linked list as empty.
- And then, traverse both the linked lists from beginning to end and compare the current nodes of both the linked lists and insert the smaller of two at the beginning of the resultant linked list.
- Finally, our resultant linked list will have the merged list in reverse order.
The following algorithm will explain the approach in detail.
Algorithm To Merge 2 Sorted Linked List In Reverse Order
-
First, initialize the resultant linked list result as an empty list.
-
Let h1 and h2 be the two pointers pointing to the head of list 1 and list 2, respectively.
-
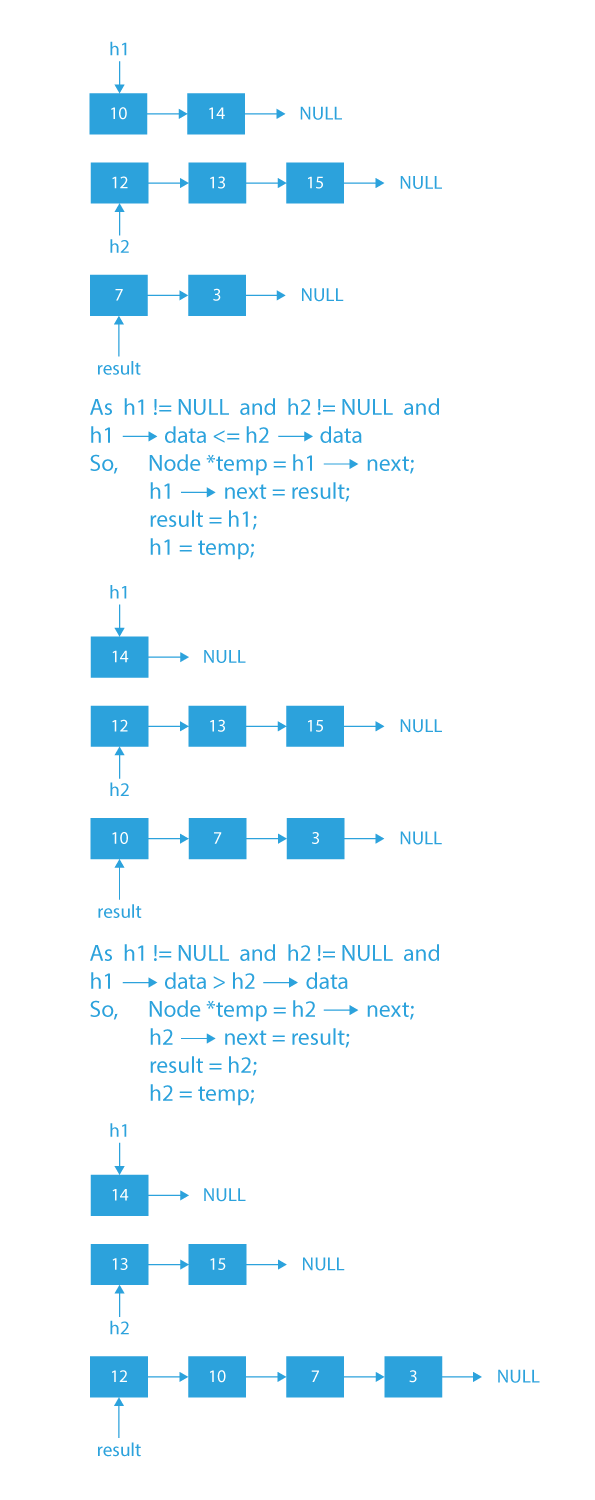
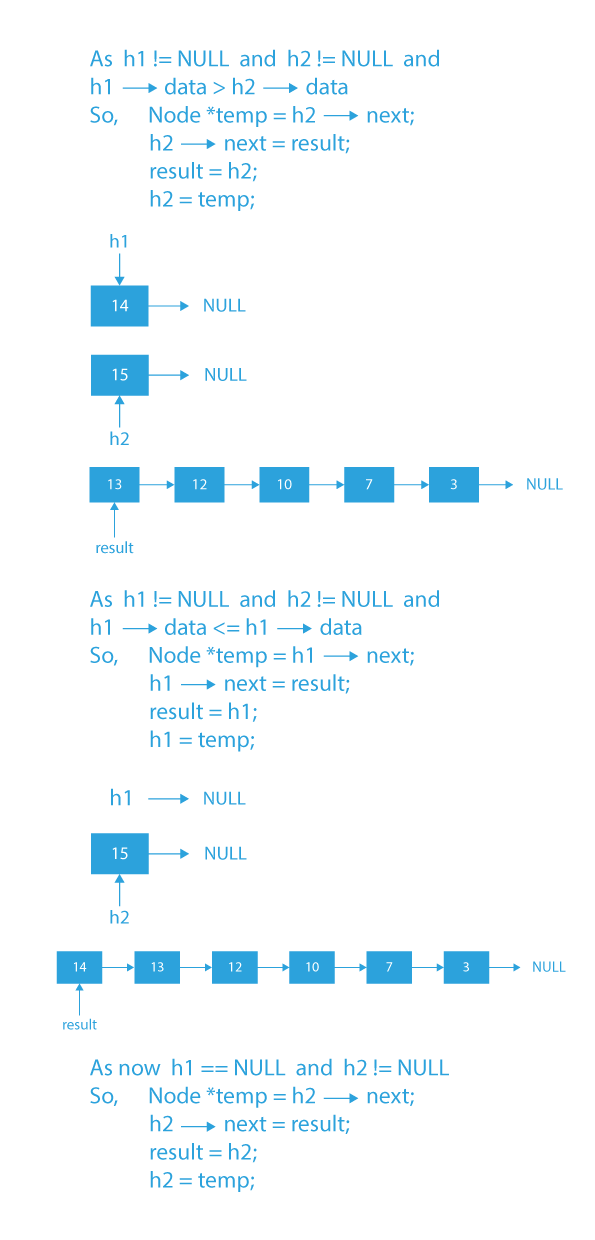
Now we will traverse the two given linked lists while(h1!=NULL && h2!=NULL).
- We will find the smaller of two nodes pointed by h1 and h2.
- After finding the smaller of the two nodes, we will insert the node with the smaller value at the front of the result list.
- Then we will move forward in the linked list with a smaller node value.
-
If either of the linked lists is traversed completely, then insert all the remaining nodes of another list into the result list.
-
Finally, after all these steps, we will have our merged list in reverse order.
Dry Run To Merge 2 Sorted Linked List In Reverse Order
Code Implementation To Merge 2 Sorted Linked List In Reverse Order
#include<stdio.h>
#include<stdlib.h>
#include <stddef.h>
struct Node
{
int key;
struct Node* next;
};
// Given two non-empty linked lists 'a' and 'b'
struct Node* SortedMerge(struct Node *a,struct Node *b)
{
// If both lists are empty
if (a==NULL && b==NULL) return NULL;
// Initialize head of resultant list
struct Node *res = NULL;
// Traverse both lists while both of then
// have nodes.
while (a != NULL && b != NULL)
{
// If a's current value is smaller or equal to
// b's current value.
if (a->key <= b->key)
{
// Store next of current Node in first list
struct Node *temp = a->next;
// Add 'a' at the front of resultant list
a->next = res;
res = a;
// Move ahead in first list
a = temp;
}
// If a's value is greater. Below steps are similar
// to above (Only 'a' is replaced with 'b')
else
{
struct Node *temp = b->next;
b->next = res;
res = b;
b = temp;
}
}
// If second list reached end, but first list has
// nodes. Add remaining nodes of first list at the
// front of result list
while (a != NULL)
{
struct Node *temp = a->next;
a->next = res;
res = a;
a = temp;
}
// If first list reached end, but second list has
// node. Add remaining nodes of first list at the
// front of result list
while (b != NULL)
{
struct Node *temp = b->next;
b->next = res;
res = b;
b = temp;
}
return res;
}
/* Function to print Nodes in a given linked list */
void printList(struct Node *Node)
{
while (Node!=NULL)
{
printf("%d ",Node->key);
Node = Node->next;
}
}
/* Utility function to create a new node with
given key */
struct Node *newNode(int key)
{
struct Node* temp =
(struct Node*) malloc(sizeof(struct Node));
temp->key = key;
temp->next = NULL;
return temp;
}
/* Driver program to test above functions*/
int main()
{
/* Start with the empty list */
struct Node* res = NULL;
/* Let us create two sorted linked lists to test
the above functions. Created lists shall be
a: 5->10->15
b: 2->3->20 */
struct Node *a = newNode(5);
a->next = newNode(10);
a->next->next = newNode(15);
struct Node *b = newNode(2);
b->next = newNode(3);
b->next->next = newNode(20);
printf("List A before merge: \n");
printList(a);
printf("\nList B before merge: \n");
printList(b);
/* merge 2 increasing order LLs in decreasing order */
res = SortedMerge(a, b);
printf("\nMerged Linked List is: \n");
printList(res);
return 0;
}
#include<iostream>
using namespace std;
/* Node structure of linked list node */
struct Node
{
int data;
struct Node* next;
};
/* Using this function we will be merging both the linked list in such a way that merged list will be in reverse order */
Node* MergeSortedReverse(Node *h1, Node *h2)
{
if (h1==NULL && h2==NULL) return NULL;
Node *result = NULL;
while (h1 != NULL && h2 != NULL)
{
if (h1->data <= h2->data)
{
Node *temp = h1->next;
h1->next = result;
result = h1;
h1 = temp;
}
else
{
Node *temp = h2->next;
h2->next = result;
result = h2;
h2 = temp;
}
}
while (h1 != NULL)
{
Node *temp = h1->next;
h1->next = result;
result = h1;
h1 = temp;
}
while (h2 != NULL)
{
Node *temp = h2->next;
h2->next = result;
result = h2;
h2 = temp;
}
return result;
}
/* Using this function we will be printing the linked list content */
void PrintingList(struct Node *Node)
{
while (Node!=NULL)
{
cout<<Node->data<<" -> ";
Node = Node->next;
}
cout<<"NULL"<<endl;
}
/* Using this function we will creating a new list node */
Node *newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->next = NULL;
return temp;
}
int main()
{ struct Node* result = NULL;
Node *list1 = newNode(3);
list1->next = newNode(7);
list1->next->next = newNode(10);
list1->next->next->next = newNode(14);
Node *list2 = newNode(12);
list2->next = newNode(13);
list2->next->next = newNode(15);
cout<<"Original linked list 1: "<<endl;
PrintingList(list1);
cout<<"Original linked list 2: "<<endl;
PrintingList(list2);
result = MergeSortedReverse(list1, list2);
cout<<"Merged list in reverse order: "<<endl;
PrintingList(result);
return 0;
}
class ReverseMerge
{
Node head;
Node a;
Node b;
/* Node Class */
static class Node
{
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
void printlist(Node node) {
while (node != null) {
System.out.print(node.data + " ");
node = node.next;
}
}
Node sortedmerge(Node node1, Node node2) {
// if both the nodes are null
if (node1 == null && node2 == null) {
return null;
}
// resultant node
Node res = null;
// if both of them have nodes present traverse them
while (node1 != null && node2 != null) {
// Now compare both nodes current data
if (node1.data <= node2.data) {
Node temp = node1.next;
node1.next = res;
res = node1;
node1 = temp;
} else {
Node temp = node2.next;
node2.next = res;
res = node2;
node2 = temp;
}
}
while (node1 != null) {
Node temp = node1.next;
node1.next = res;
res = node1;
node1 = temp;
}
while (node2 != null) {
Node temp = node2.next;
node2.next = res;
res = node2;
node2 = temp;
}
return res;
}
public static void main(String[] args) {
ReverseMerge list = new ReverseMerge();
Node result = null;
list.a = new Node(5);
list.a.next = new Node(10);
list.a.next.next = new Node(15);
list.b = new Node(2);
list.b.next = new Node(3);
list.b.next.next = new Node(20);
System.out.println("List a before merge :");
list.printlist(list.a);
System.out.println("");
System.out.println("List b before merge :");
list.printlist(list.b);
// merge two sorted linkedlist in decreasing order
result = list.sortedmerge(list.a, list.b);
System.out.println("");
System.out.println("Merged linked list : ");
list.printlist(result);
}
}
# Node of a linked list
class Node:
def __init__(self, next = None, data = None):
self.next = next
self.data = data
def SortedMerge(a,b):
if (a == None and b == None):
return None
res = None
while (a != None and b != None):
if (a.key <= b.key):
temp = a.next
a.next = res
res = a
a = temp
else:
temp = b.next
b.next = res
res = b
b = temp
while (a != None):
temp = a.next
a.next = res
res = a
a = temp
while (b != None):
temp = b.next
b.next = res
res = b
b = temp
return res
def printList(Node):
while (Node != None):
print( Node.key, end = " ")
Node = Node.next
def newNode( key):
temp = Node()
temp.key = key
temp.next = None
return temp
res = None
a = newNode(3)
a.next = newNode(7)
a.next.next = newNode(10)
a.next.next.next = newNode(14)
b = newNode(12)
b.next = newNode(13)
b.next.next = newNode(15)
print( "Original linked list 1:")
printList(a)
print( "\nOriginal linked list 2:")
printList(b)
res = SortedMerge(a, b)
print("\nMerged list in reverse order:")
printList(res)
Output
Original linked list 1:
3 -> 7 -> 10 -> 14 -> NULL
Original linked list 2:
12 -> 13 -> 15 -> NULL
Merged list in reverse order:
15 -> 14 -> 13 -> 12 -> 10 -> 7 -> 3 -> NULLTime Complexity To Merge 2 Sorted Linked List In Reverse Order: O(max(m,n)), where m, n are the size of Linked Lists.
Conclusion
In conclusion, merging two sorted linked lists in reverse order is a skillful maneuver that combines the principles of sorting and linked list manipulation. Through careful consideration of the elements in the linked lists, the merging process unfolds in a way that creates a new list with the desired reversed order. This not only requires attention to the logical flow of the data but also an understanding of pointers and node manipulation. As you embark on your journey of coding and problem-solving, the ability to merge and manipulate linked lists in reverse order will undoubtedly be a valuable addition to your toolkit.
FAQ related to Merge two sorted linked lists such that the merged list is in reverse order
Here are some of the FAQs related to Merge two sorted linked lists such that the merged list is in reverse order
Q1: Why would I need to merge two sorted linked lists in reverse order?
A1: Merging two sorted linked lists in reverse order can be useful in scenarios where you need the final merged list to be presented in descending order. This might be required for specific algorithms or data processing tasks.
Q2: What is the key principle behind merging two sorted linked lists in reverse order?
A2: The key principle involves systematically merging the two lists while ensuring that the resulting merged list is constructed in reverse order. This typically requires careful manipulation of pointers and nodes to achieve the desired outcome.
Q3: Are there specific algorithms or methods for merging linked lists in reverse order?
A3: Yes, there are various algorithms and approaches for merging two sorted linked lists in reverse order. One common method involves iterating through both lists, comparing elements, and appropriately linking nodes to form the merged list in reverse.
Q4: Can the same principles be applied to merge more than two sorted linked lists in reverse order?
A4: Yes, the principles of merging sorted linked lists in reverse order can be extended to merge more than two lists. The key is to apply the merging logic iteratively, considering each additional list in the process.
Q5: How does the time complexity of merging two sorted linked lists in reverse order compare to merging them in ascending order?
A5: The time complexity of merging two sorted linked lists in reverse order is generally similar to merging them in ascending order. However, the specific implementation details may introduce slight variations, and the choice of algorithm can impact overall performance.


