Last Updated on November 10, 2022 by Prepbytes

In this article we will learn how to move all occurrences of an element to end in a linked list. As we all know Linked list is a linear data structure in which elements are linked using pointers and are not stored in contiguous memory locations. Let’s try to understand how to move all occurrences of an element to end in a linked list.
Problem Statement
In this problem, we are given a linked list and a key in it. Our task is to move all the occurrences of the given key to the end of the linked list while maintaining the order of all other elements the same.
Problem Statement Understanding
Let’s try to understand how we can move all occurrences of an element to end in a linked list with help of examples.
Let’s say, we are given a linked list:

Then according to the problem statement, we have to move all the occurrences of the key to the end of the linked list, and also we have to maintain the order of all other elements except the key same as their order in the original given linked list. So after moving all the occurrences of the key to the end, our final resultant linked list would look something like this:

While forming the resultant linked list, first all the other elements except B will come in the same order as they were in the original linked list forming A→C→C and then all the occurrences of the B will be appended at the end of A→C→C forming A→C→C→B→B→B.
Explanation: In our final resultant linked list, we can see that all the occurrence of the key B has been moved to the end of the linked list, preserving the order of the rest of the elements of the list.
Some other examples
Input:

Output:

Input:

Output:

Now I think from the above examples it is clear how we can move all occurrences of an element to end in a linked list. So next we have to think about how we can approach this problem towards a solution?
Let’s have a glance at the approach to move all occurrences of an element to end in a linked list.
Approach 1 to move all occurrences of an element to end in a linked list
A simple approach is the brute force approach.
In this approach, we will be finding every occurrence of the given key element in the list.
- For each occurrence of the given key element in the list, we move it to the end of the linked list.
This way, all occurrences of the given key element will be moved to the end of the linked list, and we will be successful in achieving our objective of moving all the occurrences of the given key to the end of the linked list.
Time Complexity: The worst case complexity of this brute force approach is O(N*N), where N is the total number of nodes in the linked list, as for each occurrence of the key element in the list, we take approx O(N) time for the traversal to the end of the linked list and then appending the key at the end.
Space Complexity: O(1), as no additional space is used.
Although we were able to achieve our objective still the time complexity was of order N2. So now we will try to think about how can we reduce this complexity. Is a lesser time complexity solution possible? If possible, what do we have to use to convert our above O(N2) solution into an efficient lesser time complexity solution?
Now in the next approach to move all occurrences of an element to end in a linked list we will see how using pointers we can reduce the complexity.
Approach 2 to move all occurrences of an element to end in a linked list
The time complexity of the previous approach can be optimized if we make use of 2 pointers.
Let’s say the 2 pointers are p1 and p2.
- p1 is the pointer to traverse the whole list one by one.
- p2 is the pointer to an occurrence of the key if a key is found, else it will be the same as p1.
The algorithm to move all occurrences of the key element to the end is explained below.
Algorithm:
- We will start both pointers from the head of the linked list.
- We move p2 only when p2 is not pointing to a key. Furthermore, we always move p1 until p1!=NULL.
- So, when p1 and p2 are not the same, we must have found a key that lies before p1. Therefore, we swap p1 and p2 and move p2 to the next location.
- The loop invariant is, after swapping data, all node values from p2 to p1 are equal to key.
- Finally, when p1==NULL we will have our result, our linked list will have all the occurrences of the key at the end of the linked list.
Note: For a better understanding go through the dry run step by step using the algorithm and code to move all occurrences of an element to end in a linked list, hopefully, you will get to know better what we are doing in the algorithm.
Dry Run to move all occurrences of an element to end in a linked list

Code Implementation to move all occurrences of an element to end in a linked list
#include <stdio.h>
#include<stdlib.h>
struct Node {
int data;
struct Node* next;
};
struct Node* newNode(int a)
{
struct Node* temp =
(struct Node*) malloc(sizeof(struct Node));
temp->data = a;
temp->next = NULL;
}
void printList(struct Node* head)
{
struct Node* temp = head;
while (temp != NULL) {
printf("%d",&temp->data);
temp = temp->next;
}
printf("\n");
}
void moveToEnd(struct Node* head, int key)
{
struct Node* p1 = head;
struct Node* p2 = head;
while (p1 != NULL) {
if (p1 != p2 && p1->data != key) {
p2->data = p1->data;
p1->data = key;
p2 = p2->next;
}
if (p2->data != key)
p2 = p2->next;
p1 = p1->next;
}
}
int main()
{
struct Node* head = newNode(5);
head->next = newNode(2);
head->next->next = newNode(2);
head->next->next->next = newNode(7);
head->next->next->next->next = newNode(2);
head->next->next->next->next->next = newNode(2);
head->next->next->next->next->next->next = newNode(2);
printf("Before moveToEnd(), the Linked list is\n");
printList(head);
int key = 2;
moveToEnd(head, key);
printf("\nAfter moveToEnd(), the Linked list is\n");
printList(head);
return 0;
}
#include <bits stdc++.h>
using namespace std;
struct Node {
int data;
struct Node* next;
};
struct Node* newNode(int a)
{
Node* temp = new Node;
temp->data = a;
temp->next = NULL;
}
void printList(Node* head)
{
struct Node* temp = head;
while (temp != NULL) {
cout << temp->data;
temp = temp->next;
}
printf("\n");
}
void moveToEnd(Node* head, int key)
{
struct Node* p1 = head;
struct Node* p2 = head;
while (p1 != NULL) {
if (p1 != p2 && p1->data != key) {
p2->data = p1->data;
p1->data = key;
p2 = p2->next;
}
if (p2->data != key)
p2 = p2->next;
p1 = p1->next;
}
}
int main()
{
Node* head = newNode(5);
head->next = newNode(2);
head->next->next = newNode(2);
head->next->next->next = newNode(7);
head->next->next->next->next = newNode(2);
head->next->next->next->next->next = newNode(2);
head->next->next->next->next->next->next = newNode(2);
printf("Before moveToEnd(), the Linked list is\n");
printList(head);
int key = 2;
moveToEnd(head, key);
printf("\nAfter moveToEnd(), the Linked list is\n");
printList(head);
return 0;
}
class MoveEndI {
static class Node {
int data;
Node next;
}
static Node newNode(int x)
{
Node temp = new Node();
temp.data = x;
temp.next = null;
return temp;
}
static void printList(Node head)
{
Node temp = head;
while (temp != null) {
System.out.printf("%d ", temp.data);
temp = temp.next;
}
System.out.printf("\n");
}
// Moves all occurrences of given key to
// end of linked list.
static void moveToEnd(Node head, int key)
{
// Keeps track of locations where key
// is present.
Node pKey = head;
// Traverse list
Node pCrawl = head;
while (pCrawl != null) {
// If current pointer is not same as pointer
// to a key location, then we must have found
// a key in linked list. We swap data of pCrawl
// and pKey and move pKey to next position.
if (pCrawl != pKey && pCrawl.data != key) {
pKey.data = pCrawl.data;
pCrawl.data = key;
pKey = pKey.next;
}
// Find next position where key is present
if (pKey.data != key)
pKey = pKey.next;
// Moving to next Node
pCrawl = pCrawl.next;
}
}
// Driver code
public static void main(String args[])
{
Node head = newNode(10);
head.next = newNode(20);
head.next.next = newNode(10);
head.next.next.next = newNode(30);
head.next.next.next.next = newNode(40);
head.next.next.next.next.next = newNode(10);
head.next.next.next.next.next.next = newNode(60);
System.out.printf("Before moveToEnd(), the Linked list is\n");
printList(head);
int key = 10;
moveToEnd(head, key);
System.out.printf("\nAfter moveToEnd(), the Linked list is\n");
printList(head);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(x):
temp = Node(0)
temp.data = x
temp.next = None
return temp
def printList( head):
temp = head
while (temp != None) :
print( temp.data,end = " ")
temp = temp.next
print()
def moveToEnd(head, key):
pKey = head
pCrawl = head
while (pCrawl != None) :
if (pCrawl != pKey and pCrawl.data != key) :
pKey.data = pCrawl.data
pCrawl.data = key
pKey = pKey.next
if (pKey.data != key):
pKey = pKey.next
pCrawl = pCrawl.next
return head
head = newNode(5)
head.next = newNode(2)
head.next.next = newNode(2)
head.next.next.next = newNode(7)
head.next.next.next.next = newNode(2)
head.next.next.next.next.next = newNode(2)
head.next.next.next.next.next.next = newNode(2)
print("Before moveToEnd(), the Linked list is")
printList(head)
key = 2
head = moveToEnd(head, key)
print("After moveToEnd(), the Linked list is")
printList(head)
Output
Before moveToEnd(), the Linked list is
5 2 2 7 2 2 2
After moveToEnd(), the Linked list is

Time Complexity: O(N), as we are traversing the list only once.
Space Complexity: O(1), as no additional space is used.
Approach 3 to move all occurrences of an element to end in a linked list
Although the previous approach is an efficient one, now we will discuss one more efficient approach.
In this approach, we will make use of a pointer at the tail of the linked list. While traversing the list:
- If we find a node whose value is equal to the key, we will move that node to the last using that pointer tail.
Algorithm to move all occurrences of an element to end in a linked list
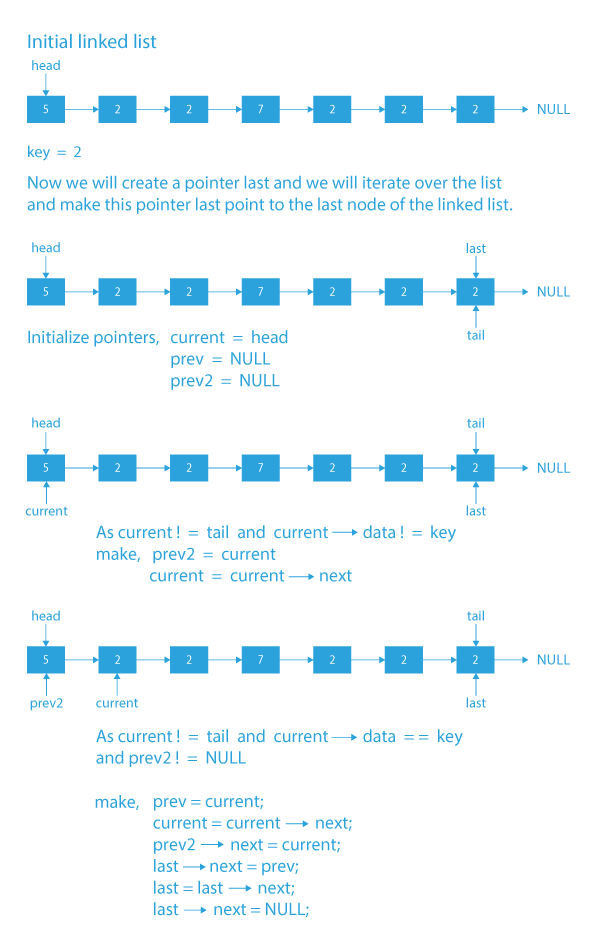
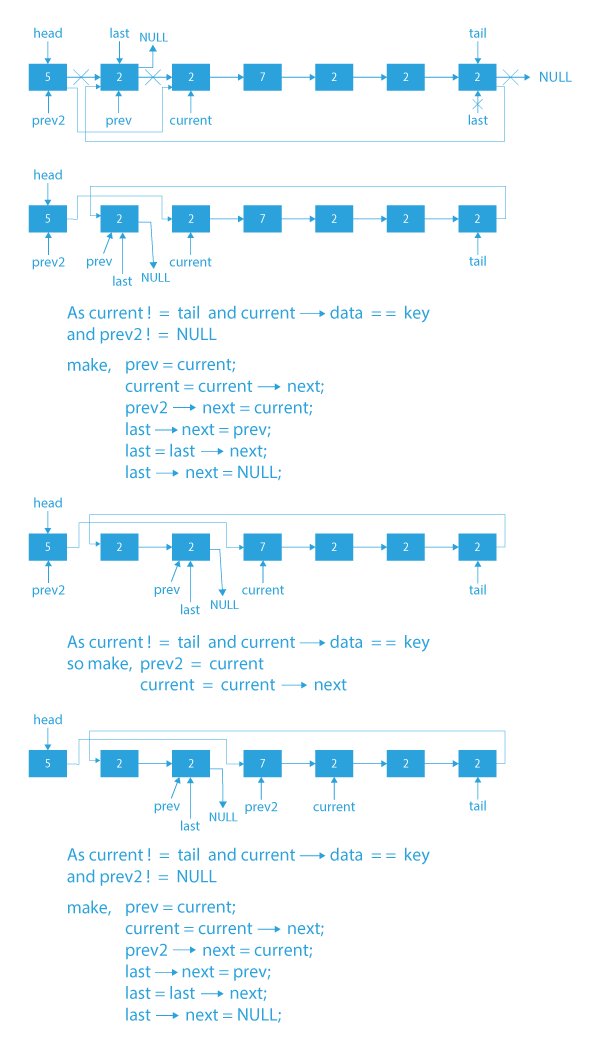
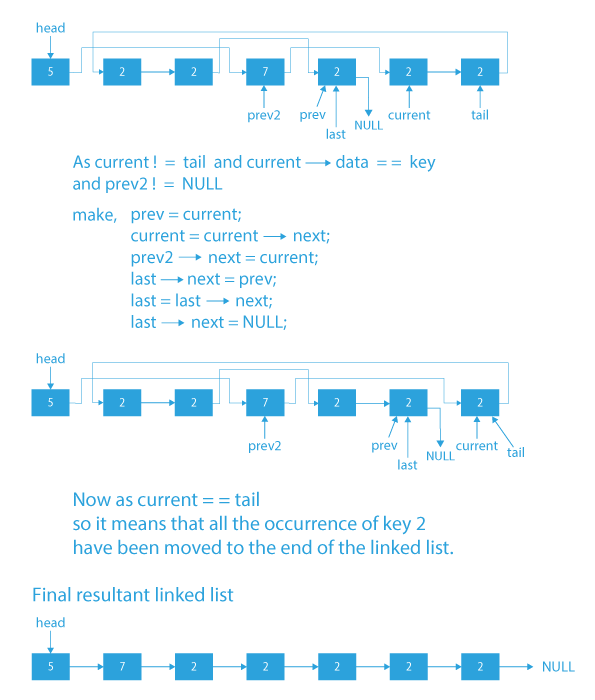
- First we will create a new pointer last, then we will traverse the linked list to the end and will make this pointer’s last point to the tail of the linked list (i.e. last node of the linked list).
- Now again while iterating over the list starting from the head using a pointer current, we will check for every node:
1) If current → data = key, then we will move the node to the end of the linked list.
2) Else we move to the next location. - Finally after the iteration is over, all the occurrences of the key will be at the end of the linked list.
Note: For a better understanding go through the dry run step by step using the algorithm and code, hopefully, you will get to know better what we are doing in the algorithm.
Dry Run to move all occurrences of an element to end in a linked list

Code Implementation to move all occurrences of an element to end in a linked list
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
struct Node* newNode(int a)
{
struct Node* temp =
(struct Node*) malloc(sizeof(struct Node));
temp->data = a;
temp->next = NULL;
}
struct Node *keyToEnd(struct Node* head, int key)
{
struct Node* tail = head;
if (head == NULL)
{
return NULL;
}
while (tail->next != NULL)
{
tail = tail->next;
}
struct Node* last = tail;
struct Node* current = head;
struct Node* prev = NULL;
struct Node* prev2 = NULL;
while (current != tail)
{
if (current->data == key && prev2 == NULL)
{
prev = current;
current = current->next;
head = current;
last->next = prev;
last = last->next;
last->next = NULL;
prev = NULL;
}
else
{
if (current->data == key && prev2 != NULL)
{
prev = current;
current = current->next;
prev2->next = current;
last->next = prev;
last = last->next;
last->next = NULL;
}
else if (current != tail)
{
prev2 = current;
current = current->next;
}
}
}
return head;
}
void printList(struct Node* head)
{
struct Node* temp = head;
while (temp != NULL)
{
printf("%d ",&temp->data);
temp = temp->next;
}
printf("\n");
}
int main()
{
struct Node* root = newNode(5);
root->next = newNode(2);
root->next->next = newNode(2);
root->next->next->next = newNode(7);
root->next->next->next->next = newNode(2);
root->next->next->next->next->next = newNode(2);
root->next->next->next->next->next->next = newNode(2);
int key = 2;
printf("Linked List before operations :");
printList(root);
printf("\nLinked List after operations :");
root = keyToEnd(root, key);
printList(root);
return 0;
}
#include<bits stdc++.h>
using namespace std;
struct Node
{
int data;
struct Node* next;
};
struct Node* newNode(int a)
{
Node* temp = new Node;
temp->data = a;
temp->next = NULL;
}
Node *keyToEnd(Node* head, int key)
{
Node* tail = head;
if (head == NULL)
{
return NULL;
}
while (tail->next != NULL)
{
tail = tail->next;
}
Node* last = tail;
Node* current = head;
Node* prev = NULL;
Node* prev2 = NULL;
while (current != tail)
{
if (current->data == key && prev2 == NULL)
{
prev = current;
current = current->next;
head = current;
last->next = prev;
last = last->next;
last->next = NULL;
prev = NULL;
}
else
{
if (current->data == key && prev2 != NULL)
{
prev = current;
current = current->next;
prev2->next = current;
last->next = prev;
last = last->next;
last->next = NULL;
}
else if (current != tail)
{
prev2 = current;
current = current->next;
}
}
}
return head;
}
void printList(Node* head)
{
struct Node* temp = head;
while (temp != NULL)
{
cout << temp->data;
temp = temp->next;
}
printf("\n");
}
int main()
{
Node* root = newNode(5);
root->next = newNode(2);
root->next->next = newNode(2);
root->next->next->next = newNode(7);
root->next->next->next->next = newNode(2);
root->next->next->next->next->next = newNode(2);
root->next->next->next->next->next->next = newNode(2);
int key = 2;
cout << "Linked List before operations :";
printList(root);
cout << "\nLinked List after operations :";
root = keyToEnd(root, key);
printList(root);
return 0;
}
class Node {
int data;
Node next;
public Node(int data)
{
this.data = data;
this.next = null;
}
}
class MoveEndIII {
static Node root;
// Function to remove key to end
public static Node keyToEnd(Node head, int key)
{
// Node to keep pointing to tail
Node tail = head;
if (head == null) {
return null;
}
while (tail.next != null) {
tail = tail.next;
}
// Node to point to last of linked list
Node last = tail;
Node current = head;
Node prev = null;
// Node prev2 to point to previous when head.data!=key
Node prev2 = null;
// loop to perform operations to remove key to end
while (current != tail) {
if (current.data == key && prev2 == null) {
prev = current;
current = current.next;
head = current;
last.next = prev;
last = last.next;
last.next = null;
prev = null;
}
else {
if (current.data == key && prev2 != null) {
prev = current;
current = current.next;
prev2.next = current;
last.next = prev;
last = last.next;
last.next = null;
}
else if (current != tail) {
prev2 = current;
current = current.next;
}
}
}
return head;
}
// Function to display linked list
public static void display(Node root)
{
while (root != null) {
System.out.print(root.data + " ");
root = root.next;
}
}
// Driver Code
public static void main(String args[])
{
root = new Node(5);
root.next = new Node(2);
root.next.next = new Node(2);
root.next.next.next = new Node(7);
root.next.next.next.next = new Node(2);
root.next.next.next.next.next = new Node(2);
root.next.next.next.next.next.next = new Node(2);
int key = 2;
System.out.println("Linked List before operations :");
display(root);
System.out.println("\nLinked List after operations :");
root = keyToEnd(root, key);
display(root);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(x):
temp = Node(0)
temp.data = x
temp.next = None
return temp
def printList( head):
temp = head
while (temp != None) :
print( temp.data,end = " ")
temp = temp.next
print()
def keyToEnd(head, key):
tail = head
if (head == None):
return None
while (tail.next != None):
tail = tail.next
last = tail
current = head
prev = None
prev2 = None
while (current != tail):
if (current.data == key and prev2 == None):
prev = current
current = current.next
head = current
last.next = prev
last = last.next
last.next = None
prev = NULL
else:
if (current.data == key and prev2 != None):
prev = current
current = current.next
prev2.next = current
last.next = prev
last = last.next
last.next = None
elif (current != tail):
prev2 = current
current = current.next
return head
head = newNode(5)
head.next = newNode(2)
head.next.next = newNode(2)
head.next.next.next = newNode(7)
head.next.next.next.next = newNode(2)
head.next.next.next.next.next = newNode(2)
head.next.next.next.next.next.next = newNode(2)
print("Linked List before operations :")
printList(head)
key = 2
head = keyToEnd(head, key)
print("Linked List after operations :")
printList(head)
Output
Linked List before operations:
5 2 2 7 2 2 2
Linked List after operations:
5 7 2 2 2 2 2
Time Complexity: O(N), as we are traversing the list twice.
So, in this article, you have learnt how to move all occurrences of an element to end in a linked list. In this we have explained three approaches with a complete picturised dry run and also provided code implementation in different languages as well.If you want to solve more questions on Linked List, you can follow this link Linked Listwhich is curated by our expert mentors at PrepBytes,.
FAQs to move all occurrences of an element to end in a linked list
1. What is the time complexity for inserting at the end of the linked list?
In a singly linked list, the time complexity for inserting and deleting an element from the list is O(n).
2. Are linked list dynamic?
Linked List is a dynamic structure, which means the list can grow or shrink depending on the data making it more powerful and flexible than Arrays. Unlike Arrays, Linked List is not stored in a contiguous memory location
3. Is linked list static?
Linked list are dynamic data structures while arrays are static data structures.


