Last Updated on November 22, 2022 by Prepbytes

We have already seen how union in linked lists work.Now in the insertion there are two linked lists which are given where we have to traverse through those lists to find a common node which is also equal. Then that node is called an intersecting node. Now in this article lets just look into the approach of intersection of two sorted linked lists
How to Intersect 2 Sorted Linked List
In this problem, we are given two sorted linked lists and are asked to print a single linked list that contains the common intersection from the two lists.
Let me make this more clear with an example test case:
Linked list 1:
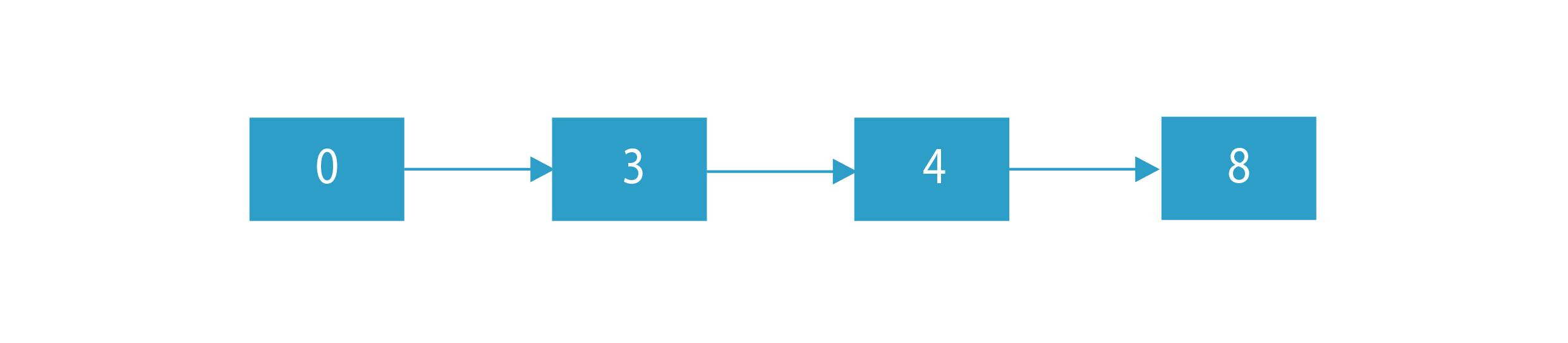
Linked list 2:

The resultant Linked List after the intersection of the above lists 1 and 2 will be:

Let’s first understand the problem statement with the help of an example:
If Linked list 1 = 0→3→4→8 and Linked list 2 = 4→8→9.
Now to find the intersection of the two linked lists, we will have to find the elements which are common in both the linked list 1 and 2 i.e. element which appear in both the lists.
- As we can see that 4 and 8 appear in both the list 1 and list 2, so they will be included in the final intersection list.
- 0, 3, 9 appears in only one of the two lists, so we will not include them in the final intersection list.
So, our final intersection list will be 4 → 8.
If Linked list 1 = 6→2→3→9 and Linked list 2 = 2→3→9.
- As we can see that 2, 3 and 9 appear in both the list 1 and list 2, so they will be included in the final intersection list.
- 6 appears in only one of the two lists, so we will not include them in the final intersection list.
So, our final intersection list will be 2 → 3 → 9.
Now, I think from the above examples, it is clear what we are trying to find in this problem. So next we will try to think how we can approach this problem.
Before jumping to the next section of the blog, try to think how you can approach this problem?
Approach 1 of intersection of two sorted linked lists
Suppose our initial linked lists are ‘a’ and ‘b’, the basic idea is to take two pointers, each pointing to the head of one of the two linked list ‘a’ and ‘b’. Now start traversing the linked lists until one of them is completely traversed and while traversing check:
- If both the elements of the lists are equal, then we need to remove both the nodes from the lists and insert the element to the tail of the dummy LinkedList.
- Otherwise, we remove the smaller element among both the linked lists.
The dummy linked list which we are referring to above, it’s main idea is to take the help of a dummy node variable that will store our final resultant list (dummy LinkedList). The pointer tail will point to the last node in the resultant list, so that the new nodes can be added easily to the resultant list. This dummy node is used as a temporary node.
When we have traversed either of the two given lists completely, then the result is in the dummy list. The values are allocated from the next node of the dummy, i.e. our resultant intersection list starts from the next of the dummy node (dummy.next).
Code Implementation of intersection of two sorted linked lists
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
struct Node {
int data;
struct Node* next;
};
void push(struct Node** head_ref, int new_data);
/*This solution uses the temporary
dummy to build up the result list */
struct Node* sortedIntersect(
struct Node* a,
struct Node* b)
{
struct Node dummy;
struct Node* tail = &dummy;
dummy.next = NULL;
/* Once one or the other
list runs out -- we're done */
while (a != NULL && b != NULL) {
if (a->data == b->data) {
push((&tail->next), a->data);
tail = tail->next;
a = a->next;
b = b->next;
}
/* advance the smaller list */
else if (a->data < b->data)
a = a->next;
else
b = b->next;
}
return (dummy.next);
}
/* UTILITY FUNCTIONS */
/* Function to insert a node at
the beginning of the linked list */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node = (struct Node*)malloc(
sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Function to print nodes in
a given linked list */
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
/* Driver program to test above functions*/
int main()
{
/* Start with the empty lists */
struct Node* a = NULL;
struct Node* b = NULL;
struct Node* intersect = NULL;
/* Let us create the first sorted
linked list to test the functions
Created linked list will be
1->2->3->4->5->6 */
push(&a, 6);
push(&a, 5);
push(&a, 4);
push(&a, 3);
push(&a, 2);
push(&a, 1);
/* Let us create the second sorted linked list
Created linked list will be 2->4->6->8 */
push(&b, 8);
push(&b, 6);
push(&b, 4);
push(&b, 2);
/* Find the intersection two linked lists */
intersect = sortedIntersect(a, b);
printf("\n Linked list containing common items of a & b \n ");
printList(intersect);
getchar();
}
#include<bits stdc++.h="">
using namespace std;
struct Node {
int data;
Node* next;
};
void push(Node** head_ref, int new_data);
Node* intersectfunc(Node* a, Node* b)
{
Node dummy;
Node* tail = &dummy;
dummy.next = NULL;
while (a != NULL && b != NULL) {
if (a->data == b->data) {
push((&tail->next), a->data);
tail = tail->next;
a = a->next;
b = b->next;
}
else if (a->data < b->data)
a = a->next;
else
b = b->next;
}
return (dummy.next);
}
void push(Node** head_ref, int new_data)
{
Node* new_node = (Node*)malloc(
sizeof(Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void show(Node* node)
{
while (node != NULL) {
cout << node->data <<" ";
node = node->next;
}
}
int main()
{
Node* a = NULL;
Node* b = NULL;
Node* intersect = NULL;
push(&a, 8);
push(&a, 4);
push(&a, 3);
push(&a, 0);
push(&b, 9);
push(&b, 8);
push(&b, 4);
intersect = intersectfunc(a, b);
show(intersect);
}
class IntersectionI
{
Node a = null;
Node b = null;
static Node dummy = null;
static Node tail = null;
static class Node
{
int data;
Node next;
Node(int data) {
this.data = data;
next = null;
}
}
void printList(Node start) {
Node p = start;
while (p != null) {
System.out.print(p.data + " ");
p = p.next;
}
System.out.println();
}
void push(int data) {
Node temp = new Node(data);
if(dummy == null) {
dummy = temp;
tail = temp;
}
else {
tail.next = temp;
tail = temp;
}
}
// function for finding intersection and adding it to dummy list
void sortedIntersect()
{
// pointers for iterating
Node p = a,q = b;
while(p != null && q != null)
{
if(p.data == q.data)
{
// add to dummy list
push(p.data);
p = p.next;
q = q.next;
}
else if(p.data < q.data)
p = p.next;
else
q= q.next;
}
}
// Driver code
public static void main(String args[])
{
IntersectionI list = new IntersectionI();
// creating first linked list
list.a = new Node(1);
list.a.next = new Node(2);
list.a.next.next = new Node(3);
list.a.next.next.next = new Node(4);
list.a.next.next.next.next = new Node(6);
// creating second linked list
list.b = new Node(2);
list.b.next = new Node(4);
list.b.next.next = new Node(6);
list.b.next.next.next = new Node(8);
// function call for intersection
list.sortedIntersect();
// print required intersection
System.out.println("Linked list containing common items of a & b");
list.printList(dummy);
}
}
class Node: def __init__(self): self.data = 0 self.next = None def sortedIntersect(a, b): dummy = Node() tail = dummy; dummy.next = None; while (a != None and b != None): if (a.data == b.data): tail.next = push((tail.next), a.data); tail = tail.next; a = a.next; b = b.next; elif(a.data < b.data): a = a.next; else: b = b.next; return (dummy.next); def push(head_ref, new_data): new_node = Node() new_node.data = new_data; new_node.next = (head_ref); (head_ref) = new_node; return head_ref def printList(node): while (node != None): print(node.data, end=' ') node = node.next; if __name__=='__main__': a = None; b = None; intersect = None; a = push(a, 8); a = push(a, 4); a = push(a, 3); a = push(a, 0); b = push(b, 9); b = push(b, 8); b = push(b, 4); intersect = sortedIntersect(a, b); printList(intersect);
Output: 4→8Time Complexity for intersection of 2 sorted linked list
: O(m+n), where m and n are the numbers of nodes in the first and second linked lists, respectively.
Space Complexity for intersection of 2 sorted linked list
: O(min(m, n)), as the output list can store at most min(m, n) nodes.
Can we solve the above problem recursively, try to think?
Approach 2 of intersection of two sorted linked lists
I can think of another approach using recursion. It will work the same way, but with a recursive function that takes two nodes and returns the intersected node list.
The most efficient idea is to compare the first elements of both the lists:
- If they are similar, then we call the recursive function with the next node of both the lists and create a node with the common node data and return it.
- Else, if they are not similar, then we remove the smaller node of both the lists and again call the recursive function.
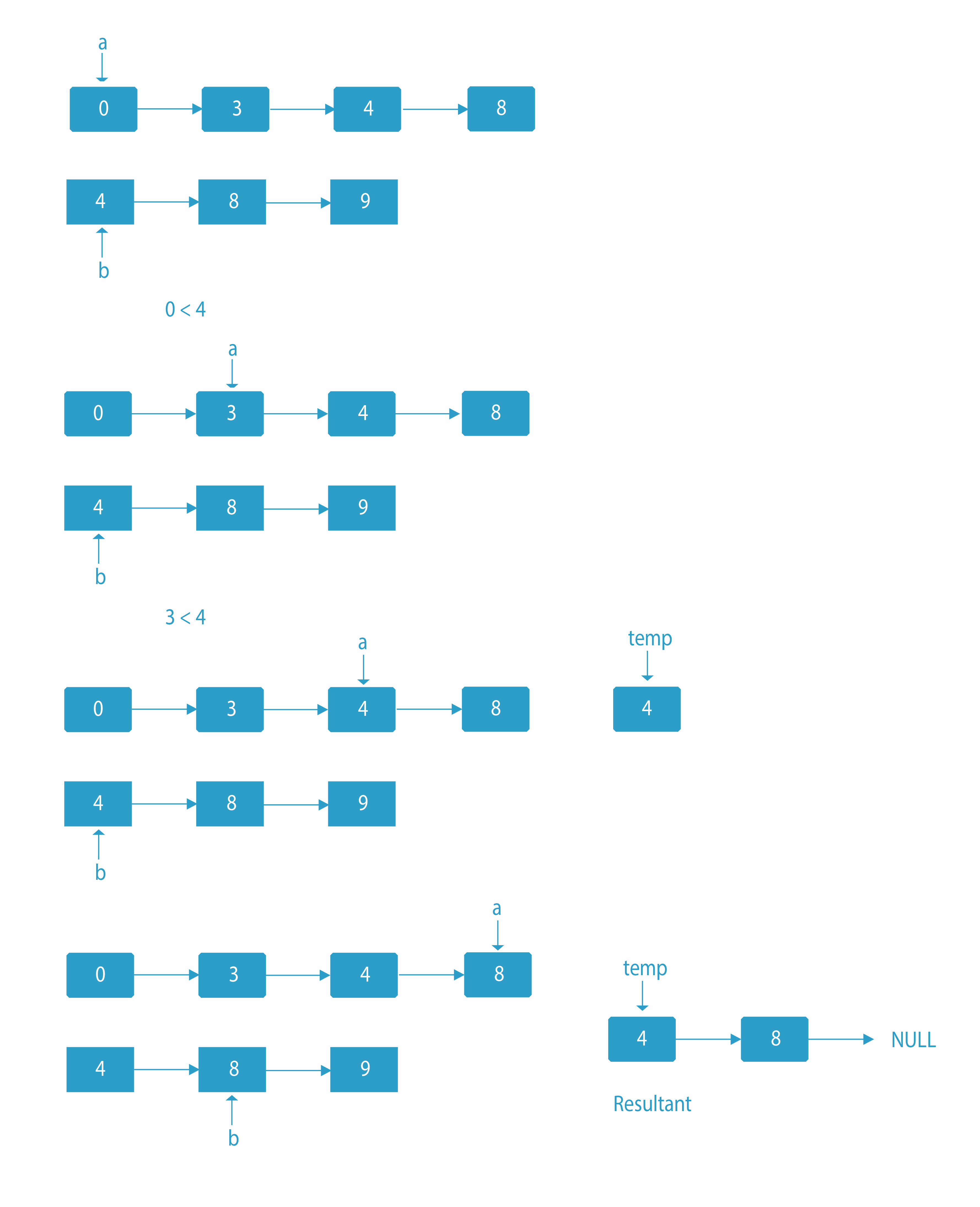
Algorithm of intersection of two sorted linked lists
Start comparing the first elements of the two linked lists:
- If two elements are similar, then create a new node with the common element and return that node and call the recursive function with the next nodes of the two lists.
- If they are different, then remove the smaller node and call the recursive function again.
Dry Run of intersection of two sorted linked lists
Code Implementation
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
struct Node {
int data;
struct Node* next;
};
struct Node* sortedIntersect(
struct Node* a,
struct Node* b)
{
/* base case */
if (a == NULL || b == NULL)
return NULL;
/* If both lists are non-empty */
/* advance the smaller list and call recursively */
if (a->data < b->data)
return sortedIntersect(a->next, b);
if (a->data > b->data)
return sortedIntersect(a, b->next);
// Below lines are executed only
// when a->data == b->data
struct Node* temp
= (struct Node*)malloc(
sizeof(struct Node));
temp->data = a->data;
/* advance both lists and call recursively */
temp->next = sortedIntersect(a->next, b->next);
return temp;
}
/* UTILITY FUNCTIONS */
/* Function to insert a node at
the beginning of the linked list */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node
= (struct Node*)malloc(
sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Function to print nodes in a given linked list */
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
/* Driver program to test above functions*/
int main()
{
/* Start with the empty lists */
struct Node* a = NULL;
struct Node* b = NULL;
struct Node* intersect = NULL;
/* Let us create the first sorted
linked list to test the functions
Created linked list will be
1->2->3->4->5->6 */
push(&a, 6);
push(&a, 5);
push(&a, 4);
push(&a, 3);
push(&a, 2);
push(&a, 1);
/* Let us create the second sorted linked list
Created linked list will be 2->4->6->8 */
push(&b, 8);
push(&b, 6);
push(&b, 4);
push(&b, 2);
/* Find the intersection two linked lists */
intersect = sortedIntersect(a, b);
printf("\n Linked list containing common items of a & b \n ");
printList(intersect);
return 0;
}
#include <bits stdc++.h="">
using namespace std;
struct Node
{
int data;
struct Node* next;
};
struct Node* intersectfunc(struct Node* a, struct Node* b)
{
if (a == NULL || b == NULL)
return NULL;
if (a->data < b->data)
return intersectfunc(a->next, b);
if (a->data > b->data)
return intersectfunc(a, b->next);
struct Node* temp = new Node();
temp->data = a->data;
temp->next = intersectfunc(a->next,b->next);
return temp;
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void show(struct Node* node)
{
while (node != NULL)
{
cout << " " << node->data;
node = node->next;
}
}
int main()
{
struct Node* a = NULL;
struct Node* b = NULL;
struct Node* intersect = NULL;
push(&a, 8);
push(&a, 4);
push(&a, 3);
push(&a, 0);
push(&b, 9);
push(&b, 8);
push(&b, 4);
intersect = intersectfunc(a, b);
show(intersect);
return 0;
}
class IntersectionII
{
static class Node
{
int data;
Node next;
};
static Node sortedIntersect(Node a,Node b)
{
// base case
if (a == null || b == null)
return null;
/* If both lists are non-empty */
/* Advance the smaller list and call recursively */
if (a.data < b.data)
return sortedIntersect(a.next, b);
if (a.data > b.data)
return sortedIntersect(a, b.next);
// Below lines are executed only when a.data == b.data
Node temp = new Node();
temp.data = a.data;
// Advance both lists and call recursively
temp.next = sortedIntersect(a.next,b.next);
return temp;
}
static Node push(Node head_ref, int new_data)
{
Node new_node = new Node();
new_node.data = new_data;
new_node.next = head_ref;
head_ref = new_node;
return head_ref;
}
static void printList(Node node)
{
while (node != null)
{
System.out.print(" " + node.data);
node = node.next;
}
}
// Driver code
public static void main(String[] args)
{
/* Start with the empty lists */
Node a = null;
Node b = null;
Node intersect = null;
a = push(a, 6);
a = push(a, 5);
a = push(a, 4);
a = push(a, 3);
a = push(a, 2);
a = push(a, 1);
/* Let us create the second sorted linked list
Created linked list will be 2.4.6.8 */
b = push(b, 8);
b = push(b, 6);
b = push(b, 4);
b = push(b, 2);
/* Find the intersection two linked lists */
intersect = sortedIntersect(a, b);
System.out.print("\n Linked list containing "+ "common items of a & b \n ");
printList(intersect);
}
}
class Node: def __init__(self): self.data = 0 self.next = None def sortedIntersect(a, b): if a == None or b == None: return if a.data < b.data: return sortedIntersect(a.next, b) if a.data > b.data: return sortedIntersect(a, b.next) temp = Node() temp.data = a.data temp.next = sortedIntersect(a.next, b.next) return temp def push(head_ref, new_data): new_node = Node() new_node.data = new_data; new_node.next = (head_ref); (head_ref) = new_node; return head_ref def printList(node): while (node != None): print(node.data, end=' ') node = node.next; if __name__=='__main__': a = None; b = None; intersect = None; a = push(a, 8); a = push(a, 4); a = push(a, 3); a = push(a, 0); b = push(b, 9); b = push(b, 8); b = push(b, 4); intersect = sortedIntersect(a, b); printList(intersect);
Output: 4→8Time Complexity for intersection of 2 sorted linked list
: O(m+n) where m and n are the numbers of nodes in the first linked list and second linked list respectively.
Space Complexity of intersection of 2 sorted linked list
: O(max(m, n)), as the output list can store at most min(m,n) nodes .
Conclusion
In the above article we tried to explain how we can find the intersection of 2 sorted linked list , which is also the common node. We have seen different approaches to traverse through the linked lists and find the intersection node. If you are interested in solving more questions of linked lists then visit the link.
Linked List.
FAQs
1. What will be the address of the second node of the linked list of which the first node is present?
The address of the second will be the address of the first with addition of the size of the first node. It all depends on the size.
2. Is there a cycle present in the linked list?
A cycle can be present in the linked list, imagine if we want to reach any node again, then we can by pointing the next of the last node to the desired node.
3. When does the loop exist in the linked list?
Generally, a loop exists in a linked list when no NULL is reached when we traverse through the link.


