Last Updated on November 4, 2022 by Prepbytes

Introduction
In the below article, we are going to see how Union is going to work with the linked lists. Generally, if we talk about the union of two linked lists, then there will be a union list which will contain all the elements from both of the lists but common elements will appear once in the union list. Let’s get into the approach of union of two linked lists and intersection of two linked lists
Problem Statement of union of two linked lists and how to find the intersection of two linked lists.
In this question, we are given two singly-linked lists. We have to find the Union and Intersection of the given lists.
Problem Statement Understanding for union and intersection of two linked lists
Union – All the elements that are in at least one of the two lists.
Intersection – Only the elements which are present in both lists.
Suppose the lists are:
L1 : 1 – > 2 – > 3
L2 : 2- > 3 – > 4
So, the union (elements that are in atleast one of the two lists) will be:
Union List: 1 – > 2 – > 3 – > 4
The intersection (elements that are present in both the lists) will be:
Intersection List: 2 – > 3
Input
L1 :
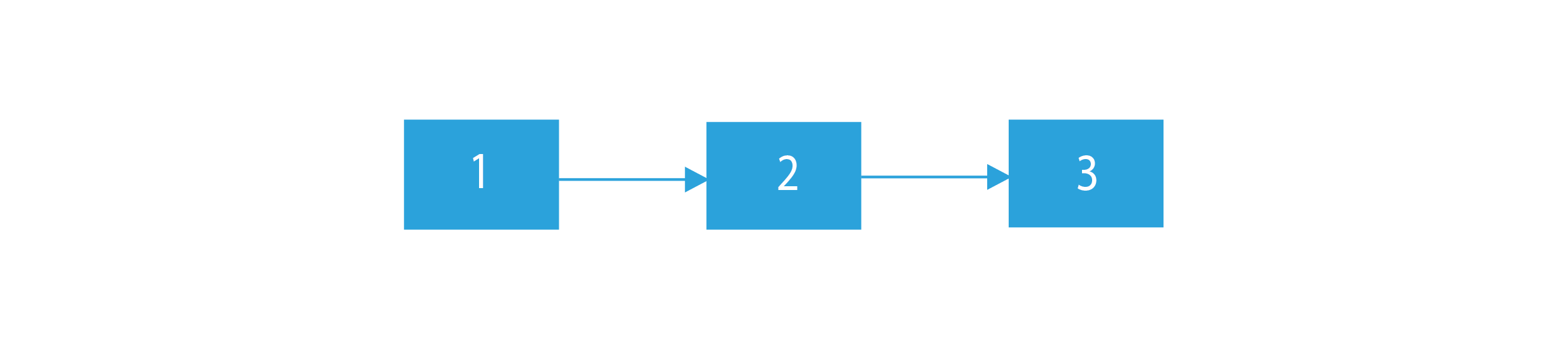
L2 :
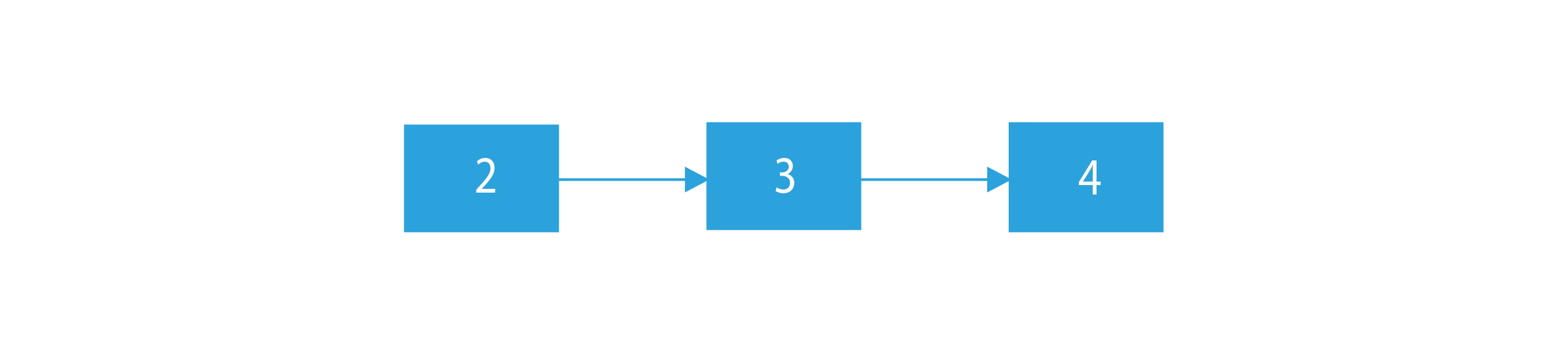
Output
Intersection List: 2 – > 3
Union List: 1 – > 2 – > 3 – > 4
Explanation: As the common elements of L1 and L2 are 2 and 3, they appear in the Intersection list. For the Union List, all the elements of L1 and L2 are considered, but no repetitions. So that’s why 2 and 3 are only present once in the union list.
While creating the lists, we do not have to worry about the order of the elements. They can be in any order.
This question is a pretty easy one. The first approach that comes to mind is to pick one element from one list, then traverse through the other list, and keep adding to output lists if necessary. But, can we do better? Yes. We can use hashing. Let us have a glance at the approaches
Approach (Nested List Traversal)for union of two linked lists
The approach is going to be pretty simple.
Intersection List – Create an empty result list. Traverse through the first list, and look for every element in the second list. If the element is present in the second list, then add that element to the result list.
Union List – Create an empty result list. Traverse through the first list and add all of its elements to the result list. Now, traverse through the second list. If an element of the second list is already present in the result list, then do not insert it into the result list, otherwise insert it.
Time Complexity of union of two linked lists – O(m*n), where m and n are the sizes of the two input lists.
Space Complexity union of two linked lists – O(1), as only temporary nodes are being created for list traversal.
There is another approach that uses hashing. The time complexity of that approach is better than the time complexity of this approach, so let us have a look at that approach as well.
Approach (Hashing)for union and intersection of two linked lists
This approach is going to use hashing. A very simple application of hashing.
Union List – Create an empty result list and an empty hash table. Traverse both the linked lists one by one. Insert every element in the hash table. Now, we will traverse through the hash table and insert all the elements in the new list. As a hash table only stores unique keys, we will automatically get the union list.
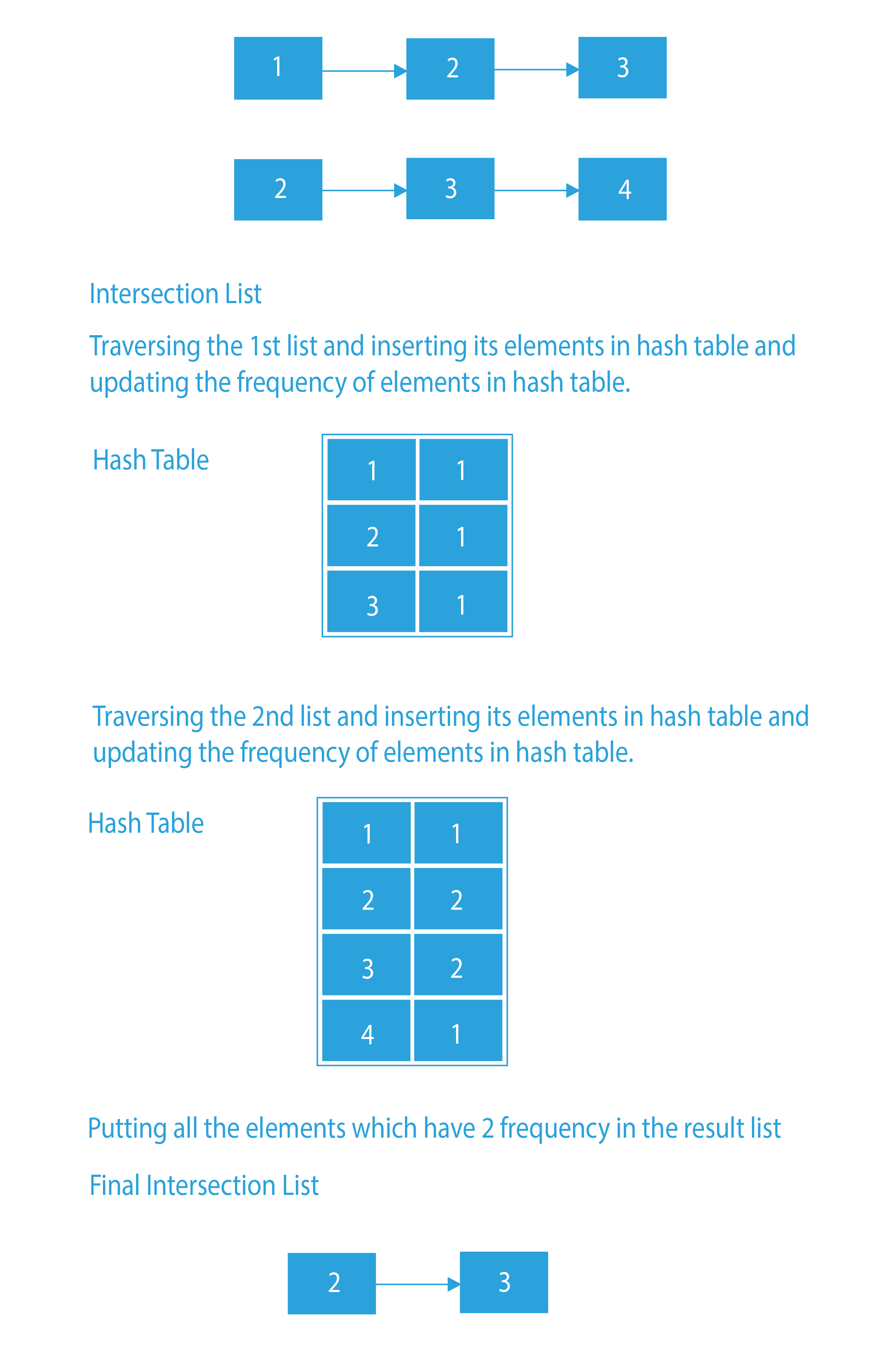
Intersection List – Create an empty result list and an empty hash table. Traverse through both the list, and increment the frequency of every element. Now, we will traverse through the hash table, and only the elements whose frequency is 2 will be inserted in the result list. As frequency 2 ensures that the element is present in both lists.
Algorithm for union and intersection of two linked lists
Union List
- Create an empty list and an empty map.
- Insert all the elements of both the lists in the map as key and their frequencies as values.
- Traverse through the map and keep pushing all the elements of the map in the result list.
- As a map only stores unique values, we will automatically get the union.
- Return the result list.
Intersection List
- Create an empty list and an empty map.
- Insert all the elements of both the lists in the map as key, and their frequencies as values
- Traverse through the map and add all those elements in the result list, whose frequency is two.
- As the frequency is two, this means that the element is present in both lists. Here, we are assuming that there are no repetitions in the given lists.
- Return the result list.
Dry Run for union and intersection of two linked lists
Union List
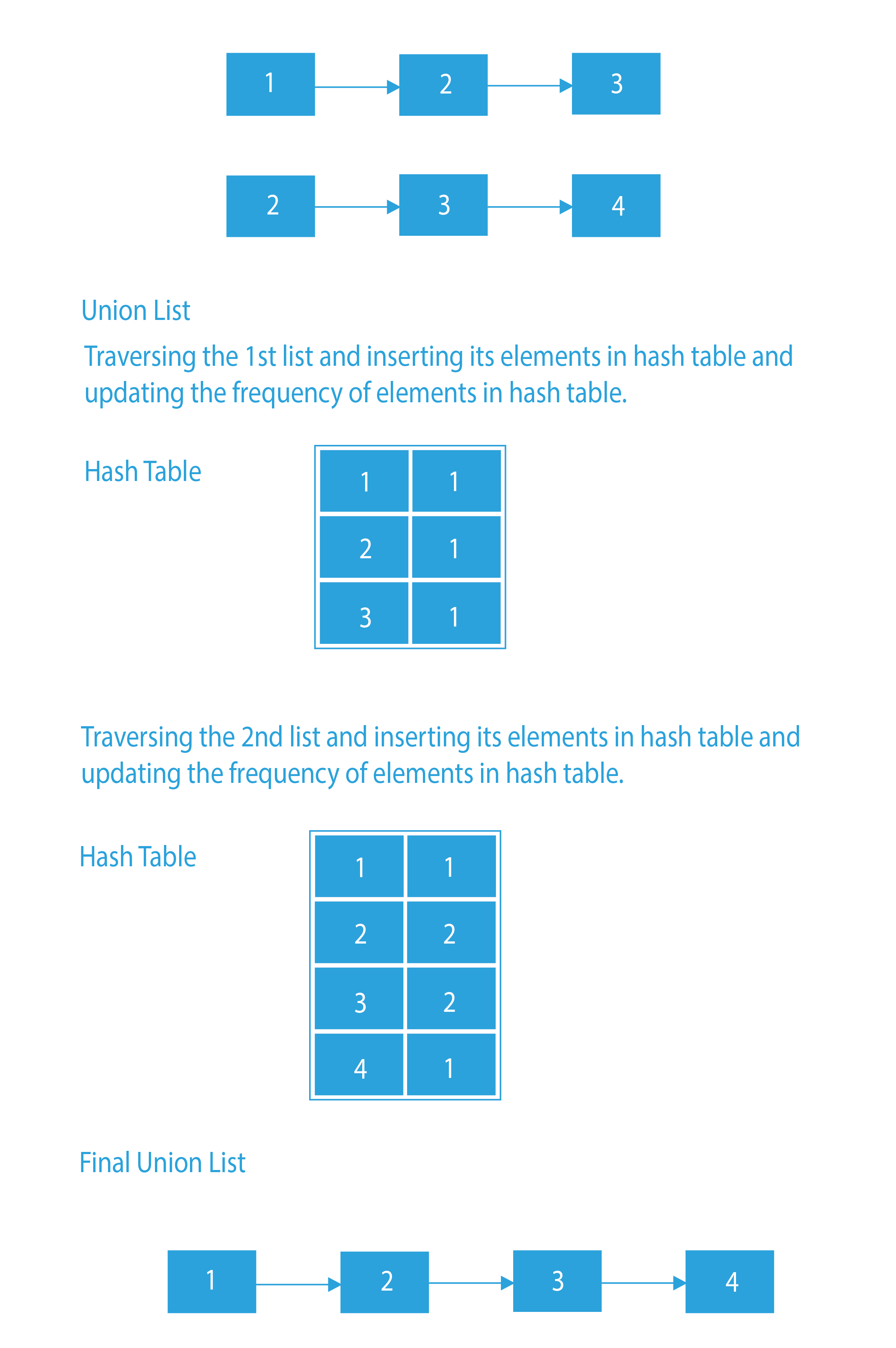
Intersection List
Code Implementation for union and intersection of two linked lists
#include <bits stdc++.h="">
using namespace std;
struct Node {
int data;
struct Node* next;
};
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = (struct Node*)malloc(
sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void storeEle(struct Node* head1, struct Node* head2,
unordered_map<int, int="">& eleOcc)
{
struct Node* ptr1 = head1;
struct Node* ptr2 = head2;
while (ptr1 != NULL || ptr2 != NULL) {
if (ptr1 != NULL) {
eleOcc[ptr1->data]++;
ptr1 = ptr1->next;
}
if (ptr2 != NULL) {
eleOcc[ptr2->data]++;
ptr2 = ptr2->next;
}
}
}
struct Node* getUnion(unordered_map<int, int=""> eleOcc)
{
struct Node* result = NULL;
for (auto it = eleOcc.begin(); it != eleOcc.end(); it++)
push(&result, it->first);
return result;
}
struct Node* getIntersection(unordered_map<int, int="">eleOcc)
{
struct Node* result = NULL;
for (auto it = eleOcc.begin();
it != eleOcc.end(); it++)
if (it->second == 2)
push(&result, it->first);
return result;
}
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
void printUnionIntersection(Node* head1, Node* head2)
{
unordered_map<int, int=""> eleOcc;
storeEle(head1, head2, eleOcc);
Node* intersection_list = getIntersection(eleOcc);
Node* union_list = getUnion(eleOcc);
printf("\nIntersection list is \n");
printList(intersection_list);
printf("\nUnion list is \n");
printList(union_list);
}
int main()
{
struct Node* head1 = NULL;
struct Node* head2 = NULL;
push(&head1, 1);
push(&head1, 2);
push(&head1, 3);
push(&head2, 2);
push(&head2, 3);
push(&head2, 4);
printf("First list is \n");
printList(head1);
printf("\nSecond list is \n");
printList(head2);
printUnionIntersection(head1, head2);
return 0;
}
public class LinkedList {
Node head;
class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
void getUnion(Node head1, Node head2)
{
Node x1 = head1, x2 = head2;
while (x1 != null) {
push(x1.data);
x1 = x1.next;
}
while (x2 != null) {
if (!isPresent(head, x2.data))
push(x2.data);
x2 = x2.next;
}
}
void getIntersection(Node head1, Node head2)
{
Node result = null;
Node x1 = head1;
while (x1 != null) {
if (isPresent(head2, x1.data))
push(x1.data);
x1 = x1.next;
}
}
void printList()
{
Node temp = head;
while (temp != null) {
System.out.print(temp.data + " ");
temp = temp.next;
}
System.out.println();
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
boolean isPresent(Node head, int data)
{
Node t = head;
while (t != null) {
if (t.data == data)
return true;
t = t.next;
}
return false;
}
public static void main(String args[])
{
LinkedList llist1 = new LinkedList();
LinkedList llist2 = new LinkedList();
LinkedList unin = new LinkedList();
LinkedList intersecn = new LinkedList();
llist1.push(1);
llist1.push(2);
llist1.push(3);
llist2.push(2);
llist2.push(3);
llist2.push(4);
intersecn.getIntersection(llist1.head, llist2.head);
unin.getUnion(llist1.head, llist2.head);
System.out.println("First List is");
llist1.printList();
System.out.println("Second List is");
llist2.printList();
System.out.println("Intersection List is");
intersecn.printList();
System.out.println("Union List is");
unin.printList();
}
}
# Python code for finding union and intersection of linkedList
class linkedList:
def __init__(self):
self.head = None
self.tail = None
def insert(self, data):
if self.head is None:
self.head = Node(data)
self.tail = self.head
else:
self.tail.next = Node(data)
self.tail = self.tail.next
class Node:
def __init__(self, data):
self.data = data
self.next = None
# return the head of new list containing the intersection of 2 linkedList
def findIntersection(head1, head2):
# creating a map
hashmap = {}
# traversing on first list
while(head1 != None):
data = head1.data
if(data not in hashmap.keys()):
hashmap[data] = 1
head1 = head1.next
# making a new linkedList
ans = linkedList()
while(head2 != None):
data = head2.data
if(data in hashmap.keys()):
# adding data to new list
ans.insert(data)
head2 = head2.next
return ans.head
# return the head of new list containing the union of 2 linkedList
def union(head1, head2):
# creating a map
hashmap = {}
# traversing on first list
while(head1 != None):
data = head1.data
if(data not in hashmap.keys()):
hashmap[data] = 1
head1 = head1.next
while(head2 != None):
data = head2.data
if(data not in hashmap.keys()):
hashmap[data] = 1
head2 = head2.next
# making a new linkedList
ans = linkedList()
# traverse on hashmap
for key, value in hashmap.items():
ans.insert(key)
return ans.head
def printList(head):
while head:
print(head.data, end=' ')
head = head.next
print()
if __name__ == '__main__':
# first list
ll1 = linkedList()
ll1.insert(1)
ll1.insert(2)
ll1.insert(3)
# second list
ll2 = linkedList()
ll2.insert(2)
ll2.insert(3)
ll2.insert(4)
print("First list is ")
printList(ll1.head)
print("Second list is ")
printList(ll2.head)
print("Intersection list is")
printList(findIntersection(ll1.head, ll2.head))
print("Union list is ")
printList(union(ll1.head, ll2.head))
Output
First List is :
3 2 1
Second List is :
4 3 2
Intersection List is :
2 3
Union List is :
4 1 2 3
Space Complexity: O(m+n), the space needed for the map (where m and n are the sizes of the given lists).
So, in this article, we have seen a detailed approach and algorithm for the union and intersection of two linked lists .This is an easy problem with many approaches. Knowing this efficient approach is very important for coding interviews. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs
- Does the order matter in linked lists?
- How are structures different from the unions?
The order in the linked lists doesn’t matter in the output list.
Structures are generally used to store distinct values in unique memory locations whereas unions manage the memory efficiently.


