Last Updated on March 28, 2022 by Ria Pathak

Concepts Used
DFS , Recursion
Difficulty Level
Hard
Problem Statement :
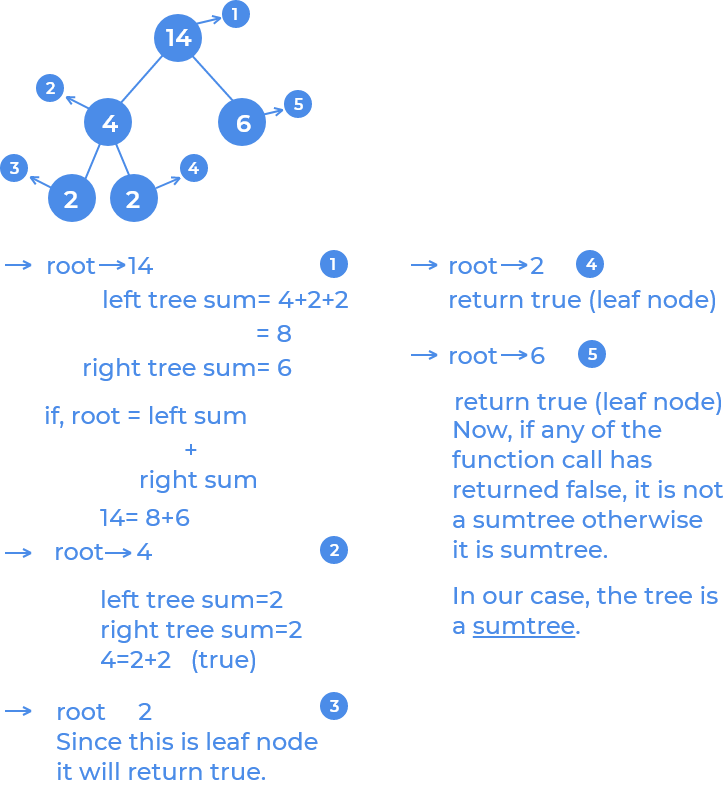
"A SumTree is a Binary Tree where the value of a node is equal to sum of the nodes present in the left subtree and right subtree."Given a binary tree and the task is to return true if given binary tree is SumTree else return false.
See original problem statement here
Solution Approach :
Introduction :
Starting from root node ,lets say
N, we will calculate the sum of the node values of left (L) & right (R) subtrees.
If,N->data = L + R, then our tree is the sumtree, else not.
Method 1 (Brute Force):
We will calculate the the sum of left & right subtree.
Now, we will compare the value of root node to the left & right subtree.
If the value of root node is equal to the value of left & right sum , then we will return true else false.We will do this recursively for our left & right subtree , by calling checkSumtree(root->left) && checkSumtree(root->right)
Method 2 (Efficient):
In the above methode, we are calculating the left & right subtrees for every node.
We can skip the recalculation of this sum for each subtree, if we take care of the following points:
If the current node is the leaf node , then the sum of the subtrees of this node is equal to the value of the node itself.
If the current node if not a leaf node, then the sum of the subtrees of this node is double the value of the node.
(See C implementation for implementation).
Complexity Analysis :
In brute-force approach, we are calculating the sum for subtree of each node. We can perform sum of the tree in O(n). Since we are calculating sum for each node so if there are
nnode we are taking O(n2) in total.
Solutions:
#include <stdio.h>
#include<stdlib.h>
#define ll long long
#define REP(i, n) for (i = 0; i < n; i++)
struct nodelist
{
ll value;
struct nodelist *left;
struct nodelist *right;
};
typedef struct nodelist node;
struct Queue
{
int front, rear, size;
unsigned capacity;
node* *array;
};
typedef struct Queue queue;
queue* createQueue(unsigned capacity)
{
queue* qu =(queue*)malloc(sizeof(queue));
qu->capacity = capacity;
qu->front = qu->size =0;
qu->rear = capacity-1;
qu->array = (node **)malloc(qu->capacity * sizeof(node));
return qu;
}
int isFull(queue* queue1)
{
return (queue1->size == queue1->capacity);
}
int isEmpty(queue* queue1)
{
return (queue1->size==0);
}
void enqueue(queue* queue1, node* item)
{
if(isFull(queue1))
return ;
queue1->rear = (queue1->rear +1 )%queue1->capacity;
queue1->array[queue1->rear] = item;
queue1->size = queue1->size +1;
}
node dequeue(queue* queue1)
{
node* item = queue1->array[queue1->front];
queue1->front = (queue1->front +1)%queue1->capacity;
queue1->size = queue1->size -1;
return *item;
}
node* front(queue* queue1)
{
return queue1->array[queue1->front];
}
node* rear(queue * queue1)
{
return queue1->array[queue1->rear];
}
node *createNode(ll value)
{
node *t= (node *) malloc(sizeof(node));
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node*t)
{
free(t);
}
node *replaceNegativeOne(node *root)
{
if(root==NULL ||(root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
void deleteTree(node *node1)
{
if(node1==NULL)
return;
deleteTree(node1->left);
deleteTree(node1->right);
free(node1);
}
node *createTreeByLevelTree()
{
ll n,m;
queue* queue1 = createQueue(100000);
node *root, *t;
root = NULL;
while(scanf("%lld", &n))
{
if(isEmpty(queue1))
{
root= createNode(n);
enqueue(queue1,root);
continue;
}
scanf("%lld", &m);
t = front(queue1);
dequeue(queue1);
t->left =createNode(n);
t->right=createNode(m);
if(t->left->value !=-1)
enqueue(queue1,t->left);
if(t->right->value !=-1)
enqueue(queue1,t->right);
if(isEmpty(queue1))
break;
}
return root;
}
int isLeaf(node *node)
{
if(node == NULL)
return 0;
if(node->left == NULL && node->right == NULL)
return 1;
return 0;
}
int checkSumTree(node* node)
{
int ls; // for sum of nodes in left subtree
int rs; // for sum of nodes in right subtree
/* If node is NULL or it's a leaf node then
return true */
if(node == NULL || isLeaf(node))
return 1;
if( checkSumTree(node->left) && checkSumTree(node->right))
{
// Get the sum of nodes in left subtree
if(node->left == NULL)
ls = 0;
else if(isLeaf(node->left))
ls = node->left->value;
else
ls = 2*(node->left->value);
if(node->right == NULL)
rs = 0;
else if(isLeaf(node->right))
rs = node->right->value;
else
rs = 2*(node->right->value);
/* If root's data is equal to sum of nodes in left
and right subtrees then return 1 else return 0*/
return(node->value == ls + rs);
}
return 0;
}
int main() {
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
if(checkSumTree(root)==1)
printf("true");
else
printf("false");
deleteTree(root);
return 0;
}
#define REP(i, n) for (i = 0; i < n; i++)
#define pb(a) push_back(a)
#define vi vector<long>
#define ll long long
#include <bits/stdc++.h>
using namespace std;
struct node
{
ll value;
node *left;
node *right;
};
node *createNode(ll value)
{
node *t = new node();
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node *t)
{
delete t;
}
node *replaceNegativeOne(node *root)
{
if (root == NULL || (root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
node *createTreeByLevelTree()
{
ll n, m;
queue<node *> q;
node *root, *t;
root = NULL;
while (cin >> n)
{
if (q.empty())
{
root = createNode(n);
q.push(root);
continue;
}
cin >> m;
t = q.front();
q.pop();
t->left = createNode(n);
t->right = createNode(m);
if (t->left->value != -1)
{
q.push(t->left);
}
if (t->right->value != -1)
{
q.push(t->right);
}
if (q.empty())
{
break;
}
}
return root;
}
void deleteTree(node *node)
{
if (node == NULL)
return;
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
int sum(struct node *root)
{
if(root == NULL)
return 0;
return sum(root->left) + root->value + sum(root->right);
}
bool checkSumTree(struct node* node)
{
if(node == NULL ||
(node->left == NULL && node->right == NULL))
return true;
return (node->value == sum(node->left)+ sum(node->right)) &&
checkSumTree(node->left) &&
checkSumTree(node->right);
}
int main()
{
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
if(checkSumTree(root))
cout<<"true"<<endl;
else
cout<<"false"<<endl;
deleteTree(root);
return 0;
}
import java.util.LinkedList;
import java.util.*;
import java.util.Scanner;
import java.io.*;
class Node
{
long value;
Node left, right;
public Node(long item)
{
value = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() {
root = null;
}
Node createNode(long value) {
Node t = new Node(value);
return t;
}
Node replaceNegativeOne(Node root) {
if (root == null || (root.value == -1 && root.left == null && root.right == null)) {
return null;
}
root.left = replaceNegativeOne(root.left);
root.right = replaceNegativeOne(root.right);
return root;
}
Node createTreeByLevelTree() {
Scanner sc = new Scanner(System.in);
long n, m;
Queue<Node> queue = new LinkedList<>();
Node t;
root = null;
while (sc.hasNext()) {
n = sc.nextLong();
if (queue.isEmpty()) {
root = createNode(n);
((LinkedList<Node>) queue).add(root);
continue;
}
m = sc.nextLong();
t = ((LinkedList<Node>) queue).peekFirst();
((LinkedList<Node>) queue).pop();
t.left = createNode(n);
t.right = createNode(m);
if (t.left.value != -1)
((LinkedList<Node>) queue).add(t.left);
if (t.right.value != -1)
((LinkedList<Node>) queue).add(t.right);
if (queue.isEmpty())
break;
}
return root;
}
void deleteTree(Node node) {
node = null;
}
long sum(Node root)
{
if(root == null)
return 0;
return sum(root.left) + root.value + sum(root.right);
}
boolean checkSumTree(Node node) {
if(node == null ||(node.left == null && node.right == null))
return true;
return (node.value == sum(node.left)+ sum(node.right)) &&
checkSumTree(node.left) &&
checkSumTree(node.right);
//write your code here
}
}
public class Main {
public static void main(String[] args) {
BinaryTree bt = new BinaryTree();
bt.root = bt.createTreeByLevelTree();
bt.root = bt.replaceNegativeOne(bt.root);
if(bt.checkSumTree(bt.root)==true)
System.out.println("true");
else
System.out.println("false");
bt.deleteTree(bt.root);
}
}
}
[forminator_quiz id="1913"]
This article tried to discuss DFS , Recursion. Hope this blog helps you understand and solve the problem. To practice more problems on DFS , Recursion you can check out MYCODE | Competitive Programming.


