Last Updated on April 8, 2022 by Ria Pathak

Concepts Used
Segment Trees
Difficulty Level
Easy
Problem Statement :
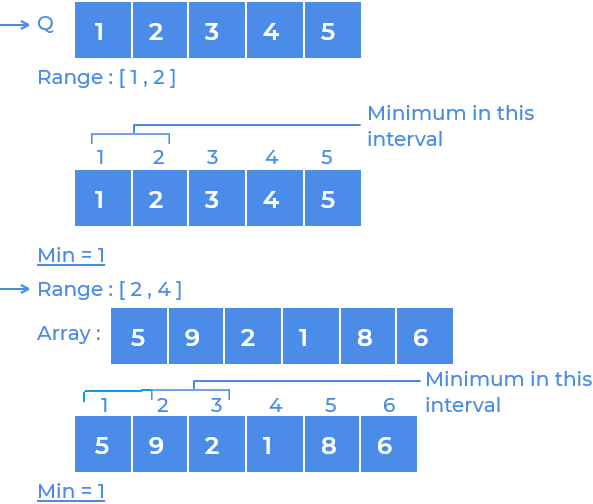
Given an array of
Nelements and Q queries. In each query he is given two valuesl,r.
We have to find the minimum value of all the elements fromltor.
See original problem statement here
Solution Approach :
Introduction :
Idea is to construct a segment tree with the leaf nodes having the array values and intermediate nodes stores the minimum value of the current subarray range.
For Example : arr{5,1,4,2,9}is our array then segment tree will store values like this ->{5,1,4,2,9}->1 , {5,1,4}-> 1, {5,1}-> 1, {5}-> 5(leaf), {1}->1 (leaf), {2,9}->2, {2}->2(leaf), {9}->9 (leaf).
Method 1 (Brute force):
We can search for the minimum value in the given range
ltorfor every query. This approach will work fine for smaller array sizes and queries, as it takes linear time to search for the minimum value for single query. As the size of the input increases this apprach will be huge drawback.
Method 2 (Segment Tree):
As the number of queries and array size is too large for linear search in every query, we will use segment tree to solve this problem.
A Segment Tree is a data structure which allows answering range queries very effectively over a large input. Each query takes logarithmic time. Range queries includes sum over a range, or finding a minimum value over a given range etc. Query be of any type we can use segment trees and modify it accordingly.
Leaf nodes of the tree stores the actual array values and intermediate nodes stores the information of subarrays with is require to solve the problem. Lets say if we have to find a sum between different ranges, so now the intermediate nodes will store the sum of the current subarray. We fill the nodes by recursively calling left and right subtree (dividing into segements), untill there is a single element left, which can be directly assigned the value of the array. Array representation of the tree is used to represent segment tree, where(i*2)+1represents the left node and(i*2)+2represents right node, parent will be represented by(i-1)/2for every indexi.We will construct our tree by starting at the original array and dividing it into two halves (left and right), untill there is a single element left (leaf) which can directly be filled with
a[i]for any indexi. Now for every range sayltor, we will store the minimum value of this range in the node.Now that our tree is constructed, we will answer queries (minimum value in the given range). The queries can be of
3types:
- The range of the tree exactly matches with the query, in this case we will return the value stored in this node.
- The range either belongs to the
leftorrightnode, in this case we will make two recursive calls forleftandrightsubtrees respectively.- The range overlaps with two of more ranges, in this case we are forced to go to the lower levels of both subtrees and find the minimum value which fits the range and finally return the least of them.
Algorithm :
construct():
- if the current node is a leaf (subarray contains single element), assign the value directly,
(tree[curr]= arr[l]).- break the tree into two halves by recursively calling for left and right subtree,
construct(l,mid)andconstruct(mid+1,r)- fill the current node with the minimum of left & right node.
(tree[curr] = min ((i*2)+1,(i*2)+2).
RMQ():
- if range is within the current range, return the value stored in node.
- if range is completely outside, return undefined.
- else return the minimum of left & right subtrees.
Complexity Analysis :
In segment tree, preprocessing time is
O(n)and worst time to for range minimum query is equivalent to the height of the tree.The space complexity is
O(n)to store the segment tree.
Solutions:
#include <stdio.h>
#include <math.h>
#include <limits.h>
#include<stdlib.h>
int minVal(int x, int y) { return (x < y)? x: y; }
int getMid(int s, int e) { return s + (e -s)/2; }
int RMQUtil(int *st, int ss, int se, int qs, int qe, int index)
{
if (qs <= ss && qe >= se)
return st[index];
if (se < qs || ss > qe)
return INT_MAX;
int mid = getMid(ss, se);
return minVal(RMQUtil(st, ss, mid, qs, qe, 2*index+1),
RMQUtil(st, mid+1, se, qs, qe, 2*index+2));
}
int RMQ(int *st, int n, int qs, int qe)
{
if (qs < 0 || qe > n-1 || qs > qe)
{
return -1;
}
return RMQUtil(st, 0, n-1, qs, qe, 0);
}
int constructSTUtil(int arr[], int ss, int se, int *st, int si)
{
if (ss == se)
{
st[si] = arr[ss];
return arr[ss];
}
int mid = getMid(ss, se);
st[si] = minVal(constructSTUtil(arr, ss, mid, st, si*2+1),
constructSTUtil(arr, mid+1, se, st, si*2+2));
return st[si];
}
int *constructST(int arr[], int n)
{
int x = (int)(ceil(log2(n)));
int max_size = 2*(int)pow(2, x) - 1;
int *st = (int *)malloc(sizeof(int)*max_size);
constructSTUtil(arr, 0, n-1, st, 0);
return st;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
int arr[n+1];
for(int i=0;i<n;i++)
{
scanf("%d",&arr[i]);
}
int *st = constructST(arr, n+1);
int q;
scanf("%d",&q);
while(q--)
{
int l,r;
scanf("%d %d",&l,&r);
l -=1;
r -=1;
printf("%d\n",RMQ(st, n+1, l,r));
}
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int minVal(int x, int y) { return (x < y)? x: y; }
int getMid(int s, int e) { return s + (e -s)/2; }
int RMQUtil(int *st, int ss, int se, int qs, int qe, int index)
{
if (qs <= ss && qe >= se)
return st[index];
if (se < qs || ss > qe)
return INT_MAX;
int mid = getMid(ss, se);
return minVal(RMQUtil(st, ss, mid, qs, qe, 2*index+1),
RMQUtil(st, mid+1, se, qs, qe, 2*index+2));
}
int RMQ(int *st, int n, int qs, int qe)
{
// Check for erroneous input values
if (qs < 0 || qe > n-1 || qs > qe)
{
cout<<"Invalid Input";
return -1;
}
return RMQUtil(st, 0, n-1, qs, qe, 0);
}
int constructSTUtil(int arr[], int ss, int se,
int *st, int si)
{
if (ss == se)
{
st[si] = arr[ss];
return arr[ss];
}
int mid = getMid(ss, se);
st[si] = minVal(constructSTUtil(arr, ss, mid, st, si*2+1),
constructSTUtil(arr, mid+1, se, st, si*2+2));
return st[si];
}
int *constructST(int arr[], int n)
{
int x = (int)(ceil(log2(n)));
int max_size = 2*(int)pow(2, x) - 1;
int *st = new int[max_size];
constructSTUtil(arr, 0, n-1, st, 0);
return st;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int arr[n];
for(int i=0;i<n;i++)
cin>>arr[i];
int *st = constructST(arr, n);
int q;
cin>>q;
while(q--)
{
int l,r;
cin>>l>>r;
l -=1;
r-=1;
cout<<RMQ(st, n, l,r)<<endl;
}
}
return 0;
}
import java.util.*;
class Main
{
int st[]; //array to store segment tree
int minVal(int x, int y) {
return (x < y) ? x : y;
}
int getMid(int s, int e) {
return s + (e - s) / 2;
}
int RMQUtil(int ss, int se, int qs, int qe, int index)
{
if (qs <= ss && qe >= se)
return st[index];
if (se < qs || ss > qe)
return Integer.MAX_VALUE;
int mid = getMid(ss, se);
return minVal(RMQUtil(ss, mid, qs, qe, 2 * index + 1),
RMQUtil(mid + 1, se, qs, qe, 2 * index + 2));
}
int RMQ(int n, int qs, int qe)
{
if (qs < 0 || qe > n - 1 || qs > qe) {
System.out.println("Invalid Input");
return -1;
}
return RMQUtil(0, n - 1, qs, qe, 0);
}
int constructSTUtil(int arr[], int ss, int se, int si)
{
if (ss == se) {
st[si] = arr[ss];
return arr[ss];
}
int mid = getMid(ss, se);
st[si] = minVal(constructSTUtil(arr, ss, mid, si * 2 + 1),
constructSTUtil(arr, mid + 1, se, si * 2 + 2));
return st[si];
}
void constructST(int arr[], int n)
{
int x = (int) (Math.ceil(Math.log(n) / Math.log(2)));
//Maximum size of segment tree
int max_size = 2 * (int) Math.pow(2, x) - 1;
st = new int[max_size]; // allocate memory
// Fill the allocated memory st
constructSTUtil(arr, 0, n - 1, 0);
}
// Driver program to test above functions
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-->0)
{
int n =sc.nextInt();
int []arr = new int [n];
for(int i=0;i<n;i++)
arr[i] = sc.nextInt();
Main tree = new Main();
tree.constructST(arr, n);
int q = sc.nextInt();
while(q-->0)
{
int qs = sc.nextInt()-1; // Starting index of query range
int qe = sc.nextInt()-1; // Ending index of query range
System.out.println(tree.RMQ(n, qs, qe));
}
}
}
}
[forminator_quiz id="2299"]
This article tried to discuss the concept of Segment Trees. Hope this blog helps you understand and solve the problem. To practice more problems on Segment Trees you can check out MYCODE | Competitive Programming.


