Last Updated on March 23, 2022 by Ria Pathak

Concepts Used
DFS , Recursion
Difficulty Level
Medium
Problem Statement :
Given a binary tree, determine if it is a valid binary search tree (BST).
See original problem statement here
Solution Approach :
Introduction :
In binary search tree, the left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
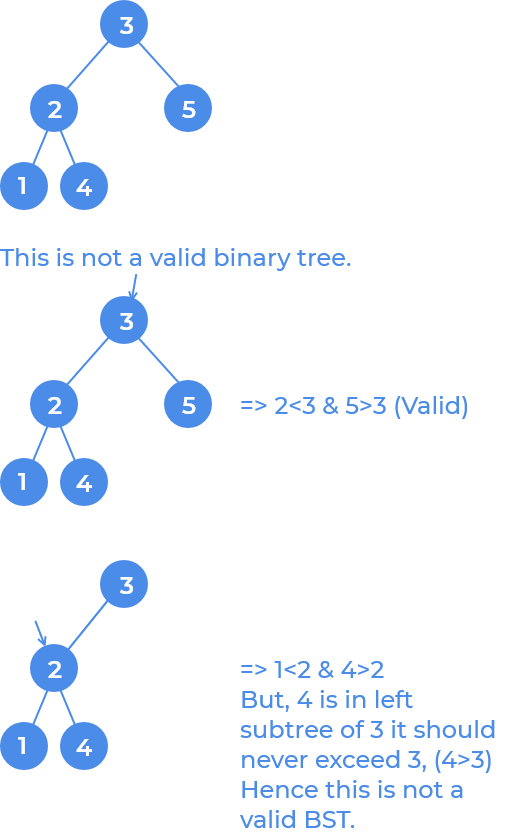
Common Mistake :
Generally, an easy approach would be for each node if we check if the left value if less than the node value & right value is greater than node value, then the tree is BST. This approach might look right but actually it is not! Suppose we are given a binary tree in which there a greater value than the root in the left subtree which also satisfies the above condition but is wrong as the left subtree cannot contain values greater than root value.
Method 1 (Simple) :
We will find maximum and mininum values for all left & right subtrees respectively.
Now we will check if the maximum value of the left subtree is less than our node value & if the minimum value of the right subtree is greater than the node value then the tree is binary search tree otherwise not.
Method 2 (Efficient) :
The above approach is simple but not very efficient.
We will now discuss a simple yet efficient approach.The idea is to traverse BST in inorder fashion as the inorder traversal of any BST gives sorted values(array). (See definition of BST).
Now, we will just maintain the previous value of the sorted array and check if the current value is greater than the previous value, for all the values, then our tree is BST otherwise not.Below is the implemention of this approach in three different languages.
Complexity Analysis :
In the first method we are finding maximum and minimum values for each node means if there are
nnodes our time complexity will be O(n2)
Solutions:
#include <stdio.h>
#include<stdlib.h>
#define ll long long
#define REP(i, n) for (i = 0; i < n; i++)
struct nodelist
{
ll value;
struct nodelist *left;
struct nodelist *right;
};
typedef struct nodelist node;
struct Queue
{
int front, rear, size;
unsigned capacity;
node* *array;
};
typedef struct Queue queue;
queue* createQueue(unsigned capacity)
{
queue* qu =(queue*)malloc(sizeof(queue));
qu->capacity = capacity;
qu->front = qu->size =0;
qu->rear = capacity-1;
qu->array = (node **)malloc(qu->capacity * sizeof(node));
return qu;
}
int isFull(queue* queue1)
{
return (queue1->size == queue1->capacity);
}
int isEmpty(queue* queue1)
{
return (queue1->size==0);
}
void enqueue(queue* queue1, node* item)
{
if(isFull(queue1))
return ;
queue1->rear = (queue1->rear +1 )%queue1->capacity;
queue1->array[queue1->rear] = item;
queue1->size = queue1->size +1;
}
node dequeue(queue* queue1)
{
node* item = queue1->array[queue1->front];
queue1->front = (queue1->front +1)%queue1->capacity;
queue1->size = queue1->size -1;
return *item;
}
node* front(queue* queue1)
{
return queue1->array[queue1->front];
}
node* rear(queue * queue1)
{
return queue1->array[queue1->rear];
}
node *createNode(ll value)
{
node *t= (node *) malloc(sizeof(node));
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node*t)
{
free(t);
}
node *replaceNegativeOne(node *root)
{
if(root==NULL ||(root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
void deleteTree(node *node1)
{
if(node1==NULL)
return;
deleteTree(node1->left);
deleteTree(node1->right);
free(node1);
}
void inOrderTraversal(node *t)
{
//write your code here;
if (t == NULL)
return;
inOrderTraversal(t->left);
printf("%d ",t->value);
inOrderTraversal(t->right);
}
node *createTreeByLevelTree()
{
ll n,m;
queue* queue1 = createQueue(100000);
node *root, *t;
root = NULL;
while(scanf("%lld", &n))
{
if(isEmpty(queue1))
{
root= createNode(n);
enqueue(queue1,root);
continue;
}
scanf("%lld", &m);
t = front(queue1);
dequeue(queue1);
t->left =createNode(n);
t->right=createNode(m);
if(t->left->value !=-1)
enqueue(queue1,t->left);
if(t->right->value !=-1)
enqueue(queue1,t->right);
if(isEmpty(queue1))
break;
}
return root;
}
int BST(struct node* node)
{
if (node == NULL)
return 1;
/* false if the max of the left is > than us */
if (node->left!=NULL && maxValue(node->left) > node->value)
return 0;
/* false if the min of the right is <= than us */
if (node->right!=NULL && minValue(node->right) < node->value)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!BST(node->left) || !BST(node->right))
return 0;
/* passing all that, it's a BST */
return 1;
}
long long int isValidBST(node *root)
{
return BST(root,0) ;
}
int main() {
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
if(isValidBST(root))
printf("%d",1);
else
printf("%d",0);
deleteTree(root);
deleteTree(root);
return 0;
}
#define REP(i, n) for (i = 0; i < n; i++)
#define pb(a) push_back(a)
#define vi vector<long>
#define ll long long
#include <bits/stdc++.h>
using namespace std;
struct node
{
ll value;
node *left;
node *right;
};
node *createNode(ll value)
{
node *t = new node();
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node *t)
{
delete t;
}
node *replaceNegativeOne(node *root)
{
if (root == NULL || (root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
node *createTreeByLevelTree()
{
ll n, m;
queue<node *> q;
node *root, *t;
root = NULL;
while (cin >> n)
{
if (q.empty())
{
root = createNode(n);
q.push(root);
continue;
}
cin >> m;
t = q.front();
q.pop();
t->left = createNode(n);
t->right = createNode(m);
if (t->left->value != -1)
{
q.push(t->left);
}
if (t->right->value != -1)
{
q.push(t->right);
}
if (q.empty())
{
break;
}
}
return root;
}
void inOrderTraversal(node *t)
{
//write your code here;
if (t == NULL)
return;
inOrderTraversal(t->left);
cout << t->value << " ";
inOrderTraversal(t->right);
}
void deleteTree(node *node)
{
if (node == NULL)
return;
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
bool BST(node *root, int prev)
{
if(root==NULL)
return true;
bool left = BST(root->left,prev);
if(root->value <= prev)
return false;
prev = root->value;
bool right = BST(root->right,prev);
return left && right;
}
bool isValidBST(node *root)
{
int prev = INT_MIN;
return BST(root,prev);
}
int main()
{
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
cout<<isValidBST(root);
deleteTree(root);
return 0;
}
import java.util.LinkedList;
import java.util.Queue;
import java.util.*;
import java.io.*;
class Node
{
long value;
Node left, right;
public Node(long item)
{
value = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() {
root = null;
}
Node createNode(long value) {
Node t = new Node(value);
return t;
}
Node replaceNegativeOne(Node root) {
if (root == null || (root.value == -1 && root.left == null && root.right == null)) {
return null;
}
root.left = replaceNegativeOne(root.left);
root.right = replaceNegativeOne(root.right);
return root;
}
void inOrderTraversal(Node node) {
//write your code here
if(node == null)
return;
inOrderTraversal(node.left);
System.out.print(node.value+" ");
inOrderTraversal(node.right);
}
Node createTreeByLevelTree() {
Scanner sc = new Scanner(System.in);
long n, m;
Queue<Node> queue = new LinkedList<>();
Node t;
root = null;
while (sc.hasNext()) {
n = sc.nextLong();
if (queue.isEmpty()) {
root = createNode(n);
((LinkedList<Node>) queue).add(root);
continue;
}
m = sc.nextLong();
t = ((LinkedList<Node>) queue).peekFirst();
((LinkedList<Node>) queue).pop();
t.left = createNode(n);
t.right = createNode(m);
if (t.left.value != -1)
((LinkedList<Node>) queue).add(t.left);
if (t.right.value != -1)
((LinkedList<Node>) queue).add(t.right);
if (queue.isEmpty())
break;
}
return root;
}
void deleteTree(Node node) {
node = null;
}
boolean BST(Node root,long prev)
{
if(root==null)
return true;
boolean left = BST(root.left,prev);
if(prev>=root.value)
return false;
prev = root.value;
boolean right = BST(root.right,prev);
return left && right;
}
boolean isValidBST(Node root)
{
return BST(root,-2);
}
}
public class Main {
public static void main(String[] args) {
// write your code here
BinaryTree bt = new BinaryTree();
bt.root = bt.createTreeByLevelTree();
bt.root = bt.replaceNegativeOne(bt.root);
if (bt.isValidBST(bt.root))
System.out.print(1);
else
System.out.print(0);
bt.deleteTree(bt.root);
}
}
[forminator_quiz id="1787"]
This article tried to discuss the concept of DFS , Recursion. Hope this blog helps you understand and solve the problem. To practice more problems on DFS , Recursion you can check out MYCODE | Competitive Programming.


